【动态规划】C++ 子序列问题（递增子序列、数对链、定差子序列、斐波那契子序列...）

1. 前言

关于 动态规划的理解 与例题，点击👇

【动态规划】C++解决斐波那契模型题目（三步问题、爬楼梯、解码方法…）

并且我们之前做过有关 子数组的dp问题：C++子数组dp问题

子序列与子数组的区别主要在于：子数组是连续的，即下标连续的不中断的；而子序列可以连续可以不连续（子序列的范围更大）。

有了上面的经验，我们来解下面 子序列 问题 ：

2. 例题

通过下面一道例题理解子序列问题，以及如何解子序列dp问题：

最长递增子序列

思路

• 题意分析
  1. 题目要求找到 最长的递增子序列的长度

根据题目要求，我们设置状态表示：

根据上面的思路，我们可以用两个for循环编写呆猫：

代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
         // 创建dp数组 + 初始化
        vector<int> dp(n, 1); // dp[i]: 以i为结尾,严格递增子序列的最长长度
        
        int ret = 1; // 结果：
        for(int i = 1; i < n; ++i)
        {
            for(int j = 0; j <= i-1; ++j)
            {
                if(nums[j] < nums[i])
                    dp[i] = max(dp[j]+1, dp[i]);
            }
            ret = max(ret, dp[i]);
        }

        return ret;
    }
};

需要注意的是：本题的最优解法并不是利用动态规划，但通过本道例题可以很好的对子序列问题进行理解：

（顺带贴上更优解法：贪心 + 二分）

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        // 贪心
        vector<int> ret;
        ret.push_back(nums[0]);

        for(int i = 0; i < nums.size(); ++i)
        {
            if(nums[i] > ret.back()) {
                ret.push_back(nums[i]);
            } else { // 二分查找
                int left = 0, right = ret.size() - 1;
                while(left < right)
                {
                    int mid = (left + right) >> 1;
                    if(ret[mid] < nums[i])
                        left = mid + 1;
                    else
                        right = mid;
                }
                ret[left] = nums[i]; // 插入
            }
        }

        return ret.size();
    }
};

---

3. 算法题

通过《最长递增子序列》一题给的经验，我们来解下面的算法题：

3.1_摆动序列

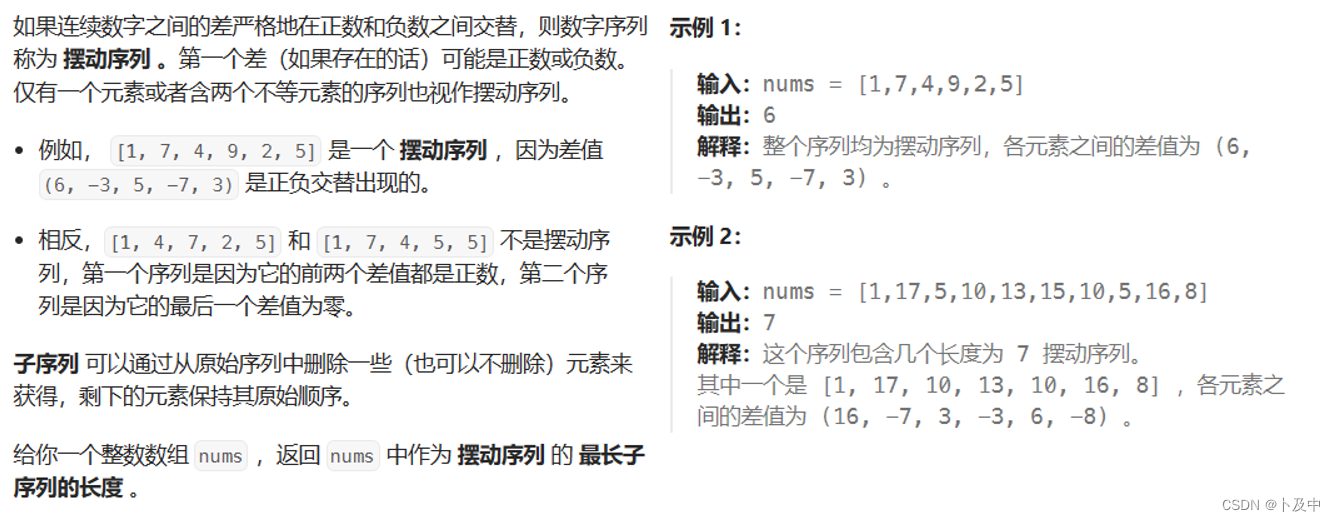
思路

• 题意分析
  1. 在子数组问题中，我们曾做过一道题《最长湍流子数组》，和本题类似，我们根据它的经验，可以创建两个dp表：

代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n = nums.size();

        // dp数组的创建 + 元素初始化
        vector<int> f(n, 1); // 以i为结尾，最后呈现“上升”状态的 子序列的最长长度
        vector<int> g(n, 1); // 以i为结尾，最后呈现“下降”状态的 子序列的最长长度

        int ret = 1; // 最终结果
        for(int i = 1; i < n; ++i)
        {
            for(int j = 0; j <= i - 1; ++j)
            {
                if(nums[j] < nums[i]) 
                    f[i] = max(g[j]+1, f[i]); // 可以将第 i 个元素加入到以第 j 个元素结尾的递增子序列中
                if(nums[j] > nums[i]) 
                    g[i] = max(f[j]+1, g[i]);
            }
            ret = max(max(f[i], g[i]), ret);
        }

        return ret;
    }
};

---

3.2_最长递增子序列的个数

思路

• 题意分析
  1. 之前的例题，求的是最长递增子序列的长度，这里要的是 最长递增子序列的 个数
  2. 即我们不仅需要考虑长度，也需要考虑个数，即两个状态，可以设置两个dp表
  3. 一个小demo： 如何找到数组中最大值的出现次数？
     • 遍历数组会有三种情况：
       • x < maxVal: 无视
       • x == maxVal: count++
       • x > maxVal: 更新maxVal，count = 0

根据这个思路，我们进行分析：

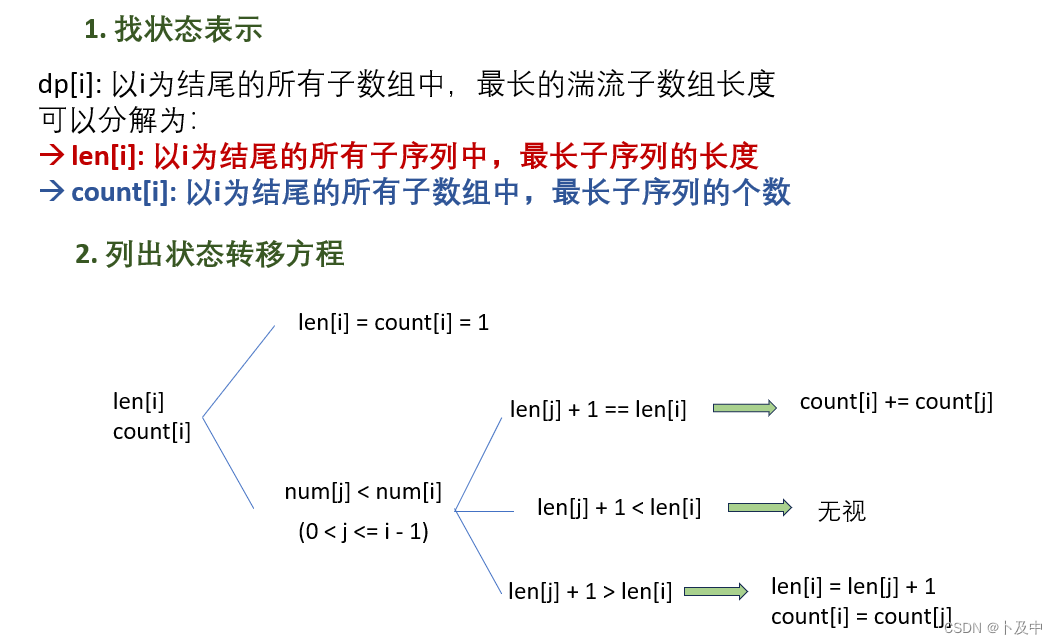
代码

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        int n = nums.size();

        // 创建dp数组 + 初始化元素
        vector<int> len(n, 1), count(n, 1); // 分别为：以i为结尾，1.递增子序列的最长长度 与 2.最长递增子序列的个数

        int retLen = 1, retCount = 1;
        for(int i = 1; i < n; ++i)
        {
            for(int j = 0; j <= i-1; ++j)
            {
                if(nums[j] < nums[i])
                {
                    if(len[j] + 1 == len[i]) count[i] += count[j]; // 第j位恰好与i组成最长递增子序列
                    // else if(len[j] + 1 < len[i]) continue; // 无视此次，可以注释掉
                    else if(len[j] + 1 > len[i]) len[i] = len[j] + 1, count[i] = count[j]; // j的递增序列更长
                }
            }
            // 更新结果
            if(retLen == len[i]) retCount += count[i];
            else if(retLen < len[i]){
                retCount = count[i];
                retLen = len[i];
            }
            // else 无视该情况
        }

        return retCount;
    }
};

---

3.3_最长数对链

思路

• 题意分析
  1. 题目要求找到 最长的数对链，数对链即对于[a, b], [c, d]仅当b < c时，才成立[a, b] -> [c, d]
  2. 根据这个规律，我们在找子序列时，首先要保证不能存在一种情况：
     • 令存在三个数对x, y, z
     • 当我们遍历到y时，即使不一定有y->z，但一定不能有z->y
  3. 根据数对链的性质，我们只需要 对数组根据首位元素进行排序 即可。
  4. 由此可以设置状态表示：

代码

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) {
        // 预处理：排序数组
        sort(pairs.begin(), pairs.end());
        
        int n = pairs.size();
         // 创建dp数组 + 初始化元素
        vector<int> dp(n, 1); // dp[i]: 以i为结尾，数对链的最长长度

        int ret = 1; // 结果
        for(int i = 1; i < n; ++i)
        {
            for(int j = 0; j <= i-1; ++j)
            {
                if(pairs[j][1] < pairs[i][0])
                {
                    dp[i] = max(dp[j] + 1, dp[i]);
                }
            }
            ret = max(ret, dp[i]);
        }

        return ret;
    }
};

---

3.4_ 最长定差子序列

思路

• 题意分析
  1. 题目要求找 最长的定差子序列的长度 ，定差子序列即等差数列，给定了公差difference。
  2. 根据题目要求设置装填表示：

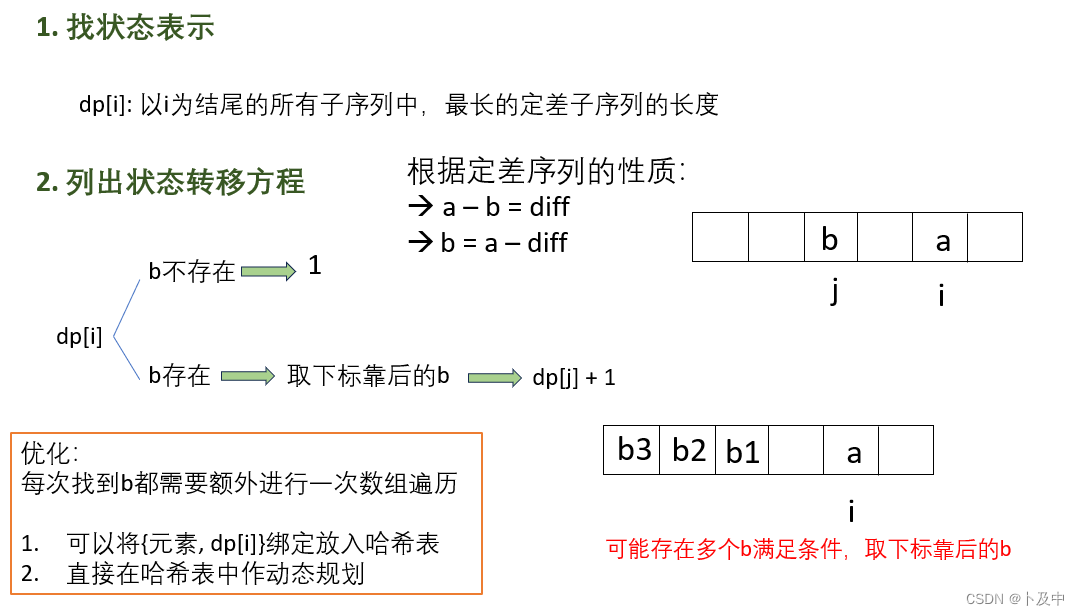
代码

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        unordered_map<int, int> hash; // arr[i] : dp[i]
        hash[arr[0]] = 1; // 初始化

        int ret = 1, n = arr.size();
        for(int i = 1; i < n; ++i)
        {
            hash[arr[i]] = hash[arr[i] - difference] + 1; // dp[i] = dp[j] + 1，可以保证是最后一个b
            ret = max(ret, hash[arr[i]]);
        }

        return ret;
    }
};

---

3.5_最长的斐波那契子序列的长度

思路

• 题意分析
  1. 题目要求找 最长的斐波那契子序列的长度
  2. 我们首先试着将状态表示设置为：
     • dp[i]：以i为结尾的所有子序列中，最长斐波那契子序列的长度
     • 当我们尝试写状态表达式时，没有办法正确找到（斐波那契子序列的判断至少需要两个元素，通过差值我们可以判断另一位是什么）
  3. 所以我们更改状态表示：

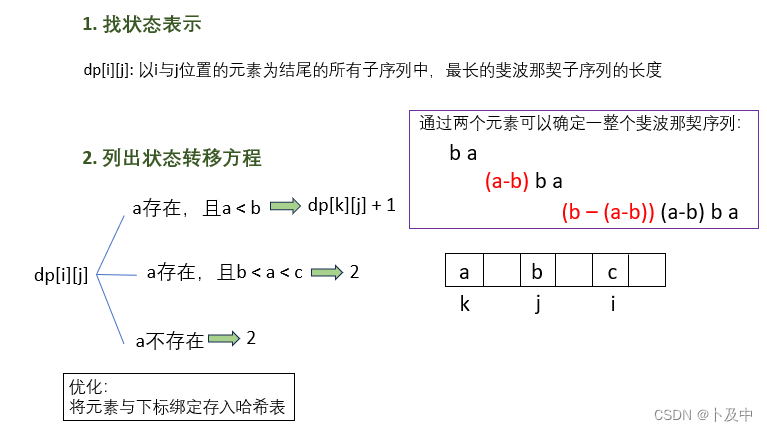
代码

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) {
        int n = arr.size();

        // 创建dp数组 + 元素初始化
        vector<vector<int>> dp(n, vector<int>(n, 2));
        // 哈希表：值映射下标
        unordered_map<int, int> hash;
        for(int i = 0; i < arr.size(); ++i)
            hash[arr[i]] = i; 

        int ret = 2; // 返回值
        for(int j = 2; j < n; ++j)
        {
            for(int i = 1; i < j; ++i)
            {
                // 填表
                int a = arr[j] - arr[i];
                if(a < arr[i] && hash.count(a))
                    dp[i][j] = dp[hash[a]][i] + 1; // 
                ret = max(ret, dp[i][j]);
            }
        }

        return ret == 2 ? 0 : ret;
    }
};

---

3.6_最长等差数列

思路

• 题意分析
  1. 本题与前面的斐波那契子序列有相似之处，下面进行状态表示的设置：

代码

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) {
        int n = nums.size();
        unordered_map<int, int> hash; // <元素 下标>
        hash[nums[0]] = 0;

        vector<vector<int>> dp(n, vector<int>(n, 2));// dp表的创建+初始化
        int ret = 2;
        for(int i = 1; i < n; ++i) // 固定倒数第二个数
        {
            for(int j = i + 1; j < n; ++j) // 固定最后一个数
            {
                int a = 2 * nums[i] - nums[j];
                if(hash.count(a))
                    dp[i][j] = dp[hash[a]][i] + 1; // dp[k][i] + 1
                ret = max(ret, dp[i][j]);
            }
            hash[nums[i]] = i; // 保存最近的元素下标 
        }
        return ret;
    }
};

---

3.7_等差数列划分II-子序列

思路

• 题意分析
  1. 前面的题要求最长等差数列的长度，而本题要求个数
  2. 对于本题我们可以采用上题思路的①优化以及①填表顺序

代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size();
        unordered_map<long long, vector<int>> hash; // <元素 下标>
        for(int i = 0; i < n; ++i) hash[nums[i]].push_back(i);

        vector<vector<long long>> dp(n, vector<long long>(n, 0));// dp表的创建+初始化
        long long sum = 0;
        for(int j = 2; j < n; ++j) // 固定倒数第二个数
        {
            for(int i = 1; i < j; ++i) // 固定最后一个数
            {
                long long a = (long long)2 * nums[i] - nums[j];
                if(hash.count(a))
                    for(auto k : hash[a])
                        if(k < i)   dp[i][j] += dp[k][i] + 1; // += dp[k][i] + 1
                sum += dp[i][j];
            }
        }
        return sum;
    }
};