CodeForces 478D-Red-Green Towers

题目

D. Red-Green Towers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are r red and g green blocks for construction of the red-green tower. Red-green tower can be built following next rules:

• Red-green tower is consisting of some number of levels;

• Let the red-green tower consist of n levels, then the first level of this tower should consist of n blocks, second level — of n - 1 blocks, the third one — of n - 2 blocks, and so on — the last level of such tower should consist of the one block. In other words, each successive level should contain one block less than the previous one;

• Each level of the red-green tower should contain blocks of the same color.

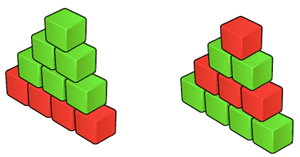
Let h be the maximum possible number of levels of red-green tower, that can be built out of r red and g green blocks meeting the rules above. The task is to determine how many different red-green towers having h levels can be built out of the available blocks.

Two red-green towers are considered different if there exists some level, that consists of red blocks in the one tower and consists of green blocks in the other tower.

You are to write a program that will find the number of different red-green towers of height h modulo 10⁹ + 7.

Input

The only line of input contains two integers r and g, separated by a single space — the number of available red and green blocks respectively (0 ≤ r, g ≤ 2·10⁵, r + g ≥ 1).

Output

Output the only integer — the number of different possible red-green towers of height h modulo 10⁹ + 7.

Examples

Input

4 6

Output

2

Input

9 7

Output

6

Input

1 1

Output

2

Note

The image in the problem statement shows all possible red-green towers for the first sample.

题义

给出r个红方块，g个绿方块，要摆出图上的那种形状，就是第i层要有i个，每层都一个颜色，而且要摆出能达到的最大高度,要求能摆出的种数。

解法

设h为最大高度，可以知道h最大是1000不到，设dp[i][j]表示从上往下，摆到第i层，红方块还剩j个的方案数，则

dp[i+1][j]=dp[i+1][j]+dp[i][j]//第i+1层不放红方块的情况

dp[i+1][j-i-1]=dp[i+1][j-i-1]+dp[i][j]//第i+1层方红方块的情况

需要滚动数组优化空间

代码

#include<cstdio>
#include<cstring>
#define mod 1000000007
int dp[2][200005],sum[1005];
int main()
{
	int r,g,i,h,j;
	scanf("%d%d",&r,&g);
	if(r==0||g==0)
	{
		printf("1\n");
		return 0;
	}
	sum[0]=0;
	for(i=1;;i++)
	{
		sum[i]=sum[i-1]+i;
		if(sum[i]>r+g)
			break;
	}
	h=i-1;
	dp[1][r]=1;
	dp[1][r-1]=1;
	for(i=1;i<h;i++)
	{
		int tmp1=i%2,tmp2=(i+1)%2;
		memset(dp[tmp2],0,sizeof(dp[tmp2]));
		for(j=0;j<=r;j++)
		{
			if(dp[tmp1][j]==0)
				continue;
			if(g-sum[i]+r-j>=i+1)
				dp[tmp2][j]=(dp[tmp2][j]+dp[tmp1][j])%mod;
			if(j>=i+1)
				dp[tmp2][j-i-1]=(dp[tmp2][j-i-1]+dp[tmp1][j])%mod;
		}
	}
	int ans=0;
	for(i=0;i<=r;i++)
		ans=(ans+dp[h%2][i])%mod;
	printf("%d\n",ans);
	return 0;
}