1到1/50的分数相加

看到一题：1+1/2+1/3+...+1/50，for循环实现；

第一想法，不就是通分嘛，有什么难的，于是开写。

#include "stdafx.h"
#include <iostream>
using namespace std;

//最大公约数
long long maxgy( long long a,long long b){
	long long tmp;
	while (a%b)
	{
		tmp = b;
		b = a%b;
		a = tmp;
	}
	return b;
}
//最小公倍数
long long mingb(long long a, long long b){
	long long tmp = maxgy(a,b);
	tmp = a*b/tmp;
	return tmp;
}
typedef struct  
{
	long long a ;
	char ch;
	long long b;
	void show(){
		cout<<a<<ch<<b<<endl;
	}
}fraction;

fraction add_fraction(fraction f1,fraction f2){
	long long j , k, l;
	fraction f;
	f.ch ='/';
	f.b=mingb(f1.b,f2.b);
	j = f.b/f1.b;
	k = f.b/f2.b;
	f.a = f1.a*j+f2.a*k;
	l = maxgy(f.a,f.b);
	f.a/=l;
	f.b/=l;
	return f;
}
int _tmain(int argc, _TCHAR* argv[])
{
	fraction f1,f2;
	f1.a=1;
	f1.ch='/';
	f1.b=1;
	f2.a=1;
	f2.ch='/';
	f2.b=1;

	for (int i =1;i<50;i++)
	{
		f2.b = i+1;
		f1=add_fraction(f1,f2);
		f1.show();
	}
	
	return 0;
}

注意到我用了long long，具体long long与_int64有啥区别，请参考http://blog.csdn.net/shiwei408/article/details/7463476

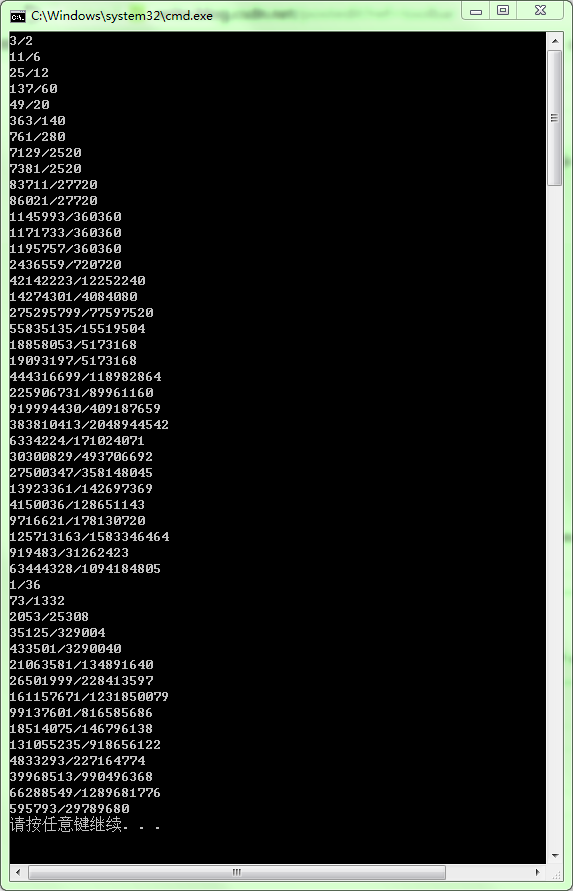
其实，我一开始是用int的，就是这个样子了，注意到，正确答案也就没几个了，为啥呢？

肯定是int的范围太小，有操作数越界了，然后我用unsigned int， long ，unsigned long，都不对

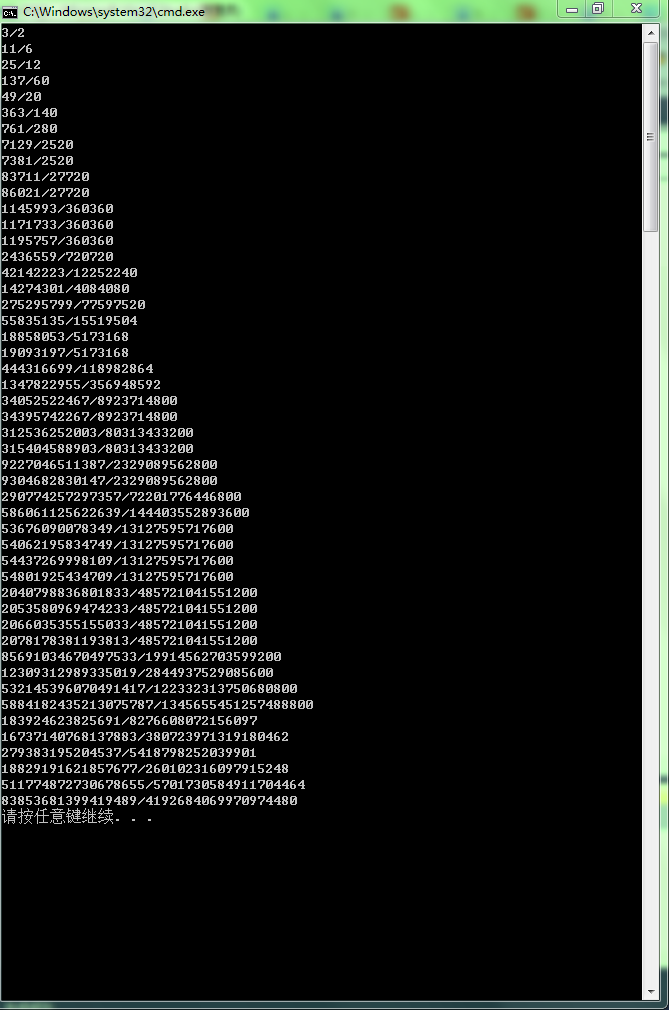
于是我祭出了大杀器——long long，说实话之前从没请过这位仁兄出场；

然后运行下

其实会发现，最后几位的结果还是不对啊，这...这...我就不知道，这个时候我重新审视这个过程，你以为你的极限是long，但是32位下，long与int其实都是4个字节，你以为unsigned一下就行了，其实不过是表示正数翻了倍而已，long long你又以为应该行了吧，但是这只是到1/50，如果到1/100呢，到1/1000呢，如果按照这种方法，总会有突破范围的那个数。

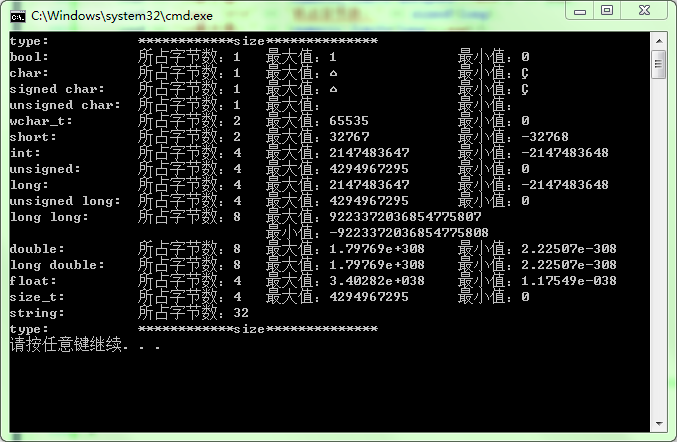
盗用一张图，来说下这些基本数据类型的范围。