LCA算法-倍增算法

前言

LCA（lowest common ancestor）问题，是初学基础数据结构——二叉树时的经典例题，对于单次求最近公共祖先我们可以在O(n)的时间复杂度内完成，但是对于多次求任意两点的最近公共祖先，显然就不是那么容易了，对于LCA问题，我们一般有两种解法——倍增算法和Tarjan算法，本文来介绍倍增算法求解LCA问题。

tarjan算法求LCA见：LCA算法-tarjan算法

---

前置知识——二进制拆分

任一自然数可以拆成若干2的幂之和

证明：设p的二进制表示下从低到高第i位为ki（i = 0 ， 1 ， 2 ……），则
$$p=\sum _{i=0}^n{2}^i\ast ki，ki=0或1$$
得证

这个性质，我们可以得出对于x和y，不妨设x < y，那么x可以通过加上若干个递增且互不相同的2次幂从而得到y

二进制拆分是倍增算法解决2次幂可划分递推问题的基础。

前置知识——ST表

关于ST表的详细原理见

之所以能用ST表就在于LCA问题其实也是一种满足结合律的可重复贡献问题。

倍增算法求LCA

LCA的运算性质

• 对于LCA(x,y)我们有
• LCA(x,x) = x
• LCA(x,y) = x，则x为y的祖先
• 如果x不为y的祖先并且y不为x的祖先，那么x，y分别处于 LCA (x，y)的两棵不同子树中
• dist(x，y) = depth(x) + depth(y) - 2 * depth(LCA(x，y))

算法原理

预处理

由于LCA问题仍是一种离线查询，所以我们可以通过ST表预处理出每个节点向上2^i层的祖先。

仍然是区间划分的问题，我们定义fa[i][j]为节点i向上2^j次方层的祖先，那么f[i][j]可以由长度减半的子区间转移过来（结合LCA的运算性质），即
$$f[i][j]=f[f[i][j-1]][j-1]$$
因为f[i][j-1]为i向上2^{(j-1)层的祖先，那么该祖先再向上2}(j-1)层的祖先的祖先就是fa[i][j]为节点i向上2^j次方层的祖先

和我们ST表预处理区间最值一样，这个过程也需要O(nlogn)的时间复杂度。

预处理代码实现

//#define N 500010
//int fa[N][20]{0}, depth[N], n, m, s, u, v;
//vector<int> edges[N];
void dfs(int x, int father)
{
    depth[x] = depth[father] + 1;
    fa[x][0] = father;
    for (int i = 1; i < 20; i++)
        fa[x][i] = fa[fa[x][i - 1]][i - 1];
    for (auto y : edges[x])
        if (y != father)
            dfs(y, x);
}
//main
//dfs(root,0);//root为根节点

查询

预处理就是要简化查询的时间复杂度，在未预处理的情况下，我们单次查询最坏可以达到O(n)的时间复杂度，那么预处理之后呢？

对于任意两个节点x，y他们的位置情况无非三种关系

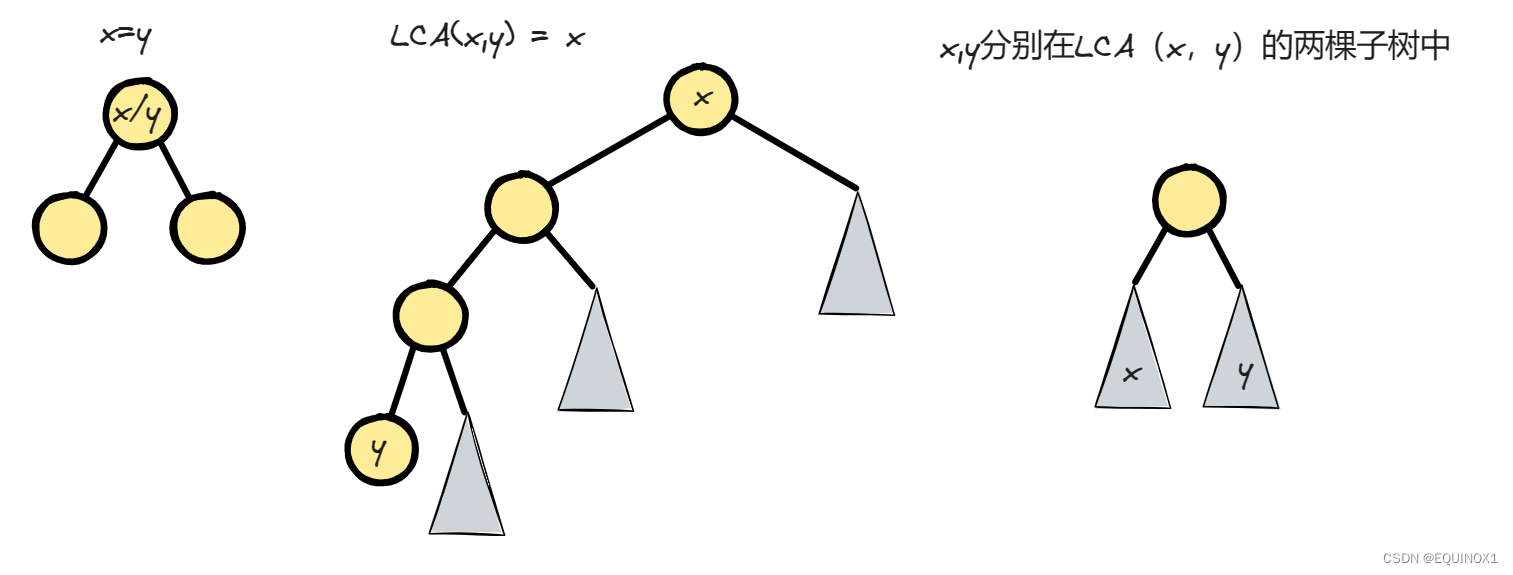
• 第一种情况不再赘述

• 第二种情况下，不妨设x为y的祖先，那么由于x、y间距离的二进制可拆性，y可以通过向上跳若干次2次幂层可以到达x或者x的下一层位置，也就是说y可以到达x的位置。

• 第三种情况下，x，y分别在LCA(x，y)的两棵子树里，如果二者深度不同，不妨设depth(x) > depth(y)，那么x可以向上跳到y的深度层，然后二者一同向上跳，二者一定会在LCA(x，y)处相遇

其实向上查询的过程就是弥补二进制位的过程

查询代码实现

实现流程

• 查询lca(x,y)，取depth[x] >= depth[y]
• 调整x到y的层次
• 如果x == y，则直接返回
• 否则，枚举调整层数，x和y一起向上调整，只要二者祖先节点不同就向上调
• 最终x，y停留在lca(x,y)的孩子节点，fa[x][0]即为所求

int lca(int x, int y)
{
    if (depth[x] < depth[y])
        swap(x, y);
    for (int i = 19; i >= 0; i--)
        if (depth[fa[x][i]] >= depth[y])
            x = fa[x][i];
    if (x == y)
        return x;
    for (int i = 19; i >= 0; i--)
        if (fa[x][i] != fa[y][i])
            x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

OJ链接

P3379 【模板】最近公共祖先（LCA） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

[P4211 LNOI2014] LCA - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)