算法学习系列（六十二）：LCA（最近公共祖先）：倍增法、Tarjan算法

lijiachang030718

于 2024-05-15 16:38:48 发布

阅读量1k

点赞数 17

分类专栏：算法文章标签：算法学习 c++ 笔记图论 LCA 程序人生

本文链接：https://blog.csdn.net/weixin_60033897/article/details/138905660

版权

算法专栏收录该内容

63 篇文章 8 订阅

订阅专栏

引言

关于这个 $L C A$ 问题蓝桥杯这两年考的是也是越来越多了，尤其是去年直接出了个裸题（模板题），也是没想到的，再加上今年省赛 $ja v a$ 组也出了一道与之相关的题，所以今年国赛感觉出的几率也是有的。学下来发现其实也没那么难，又是自己想神秘了，思路和代码总的来说都不是很难，难的是想法，这道题你能否能想到用 $L C A$ 做才是关键，所以本章内容还是采用讲题的策略来进行讲解，就其实都是非常经典的问题，几乎都是模板题，但是我觉得蓝桥杯应该不会出特别难的了，因为本身这个算法就很难，还是要多写写熟即可，继续加油吧！

一、LCA问题

LCA问题：给一棵有根的树，求任意两个结点的最近公共祖先，这里介绍常用的两种算法：倍增法、 $T a r jan$ 算法
时间复杂度：倍增法： $O (m l o g n)$ ， $T a r jan$ 算法： $O (n + m)$ ， $n$ 为结点数， $m$ 为询问次数
个人注意：其实只要结点数不是特别多，这两个算法都可以用，但是 $T a r jan$ 算法需要借助并查集，所以可能对于离散的数据就没那么好处理，我觉得如果结点编号连续就用 $T a r jan$ 算法，不连续就用倍增法

1.倍增法

倍增法：倍增法属于是在线做法，属于给一个数算一个答案
在这里插入图片描述

2.Tarjan算法

tarjan算法：属于离线做法，针对所有询问，把其全部读入，统一计算出来，再统一输出。

在这里插入图片描述

二、祖孙询问

标签：LCA、倍增法

思路：这是一道很裸的求 $L C A$ 的问题，所以直接就讲模板了。首先我们需要预处理出两个数组，分别是 $d e pt h [i], f a [i] [j]$ ，分别代表编号为 $i$ 的结点的深度，从结点 $i$ 走 $2^j$ 步所能到达的结点，我们定义根结点的深度为 $1$ ，其余结点依次递增计算，然后定义一个哨兵结点 $0$ ，并且 $d e pt h [0] = 0$ 。 $d e pt h$ 数组可以直接从根结点开始宽搜一下就行了，然后顺便求出 $f a$ 数组，有一个式子 $f a [i] [j] = f a [f a [i] [j - 1]] [j - 1]$ ，也就是先走一半再走另一半，我们可以循环遍历即可。然后求 $L C A$ 有两个步骤，首先让两个结点走到同一层，然后让两个结点同时向上走，走到倒数第二步的时候停下来，这时候它们两的父节点就是它们的最近公共祖先。这里的走有一个技巧，就是二进制的走法，因为肯定会走 $k$ 步，因为 $2^{15} = 32768$ ，并且结点最多有 $4$ 万个，所以最多有 $15$ 层，最多走 $16$ 步，也就是最多把 $16$ 个二进制位（走到哨兵结点）走完，所以根据我们可以从大往小的走，只要 $d e pt h [f a [a] [k]] >= d e pt h [b]$ 那就继续走，这样相当于设置了个条件使其一定会让 $a$ 走到和 $b$ 同一层的，也是因为步数的二进制是从大到小走的。然后就让两个点同时向上走，跟刚才的走法一样，还是按二进制的方式走，但是这次如果两个点走到相等了，不知道是否是最近的，因为是按二进制位从大到小走的，可能有的会走过了，所以我们走到两个点的 $L C A$ 的下一层，因为是按二进制位走的（相当于是所有的走法），所以肯定会存在一种走法满足条件并且走满，使得 $\neq fa[b][k]$ ，走满之后，那么 $a, b$ 的父亲就是它们的最近公共祖先，也就是 $f a [a] [0]$ 。

题目描述：

给定一棵包含 n 个节点的有根无向树，节点编号互不相同，但不一定是 1∼n。

有 m 个询问，每个询问给出了一对节点的编号 x 和 y，询问 x 与 y 的祖孙关系。

输入格式
输入第一行包括一个整数 表示节点个数；

接下来 n 行每行一对整数 a 和 b，表示 a 和 b 之间有一条无向边。如果 b 是 −1，那么 a 就是树的根；

第 n+2 行是一个整数 m 表示询问个数；

接下来 m 行，每行两个不同的正整数 x 和 y，表示一个询问。

输出格式
对于每一个询问，若 x 是 y 的祖先则输出 1，若 y 是 x 的祖先则输出 2，否则输出 0。

数据范围
1≤n,m≤4×104,1≤每个节点的编号≤4×104
输入样例：
10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19
输出样例：
1
0
0
0
2

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 4e4+10, M = N * 2, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][16];  //father
int root;

void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs()
{
	memset(depth, 0x3f, sizeof depth);
	depth[0] = 0, depth[root] = 1;
	
	queue<int> q; q.push(root);
	while(q.size())
	{
		int t = q.front(); q.pop();
		
		for(int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			if(depth[j] > depth[t] + 1)
			{
				depth[j] = depth[t] + 1;
				q.push(j);
				
				fa[j][0] = t;
				for(int k = 1; k <= 15; ++k)
				{
					fa[j][k] = fa[fa[j][k-1]][k-1];
				}
			}
		}
	}
}

int lca(int a, int b)
{
	if(depth[a] < depth[b]) swap(a,b);  // 默认a在b的下面
	for(int k = 15; k >= 0; --k)  // 让a走到b同一层
	{
		if(depth[fa[a][k]] >= depth[b])  // 如果走过头了就不走
		{
			a = fa[a][k];
		}	
	} 
	
	if(a == b) return a;
	
	for(int k = 15; k >= 0; --k)
	{
		// 因为如果相等，不能确定是否是最近的
		if(fa[a][k] != fa[b][k])  // 同时走到LCA的下一层
		{
			a = fa[a][k];
			b = fa[b][k];
		}
	}
	return fa[a][0];
}

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	memset(h, -1, sizeof h);
	cin >> n;
	for(int i = 0; i < n; ++i)
	{
		int a, b; cin >> a >> b;
		if(b == -1) root = a;
		else add(a,b), add(b,a);
	}
	
	bfs();
	
	cin >> m;
	while(m--)
	{
		int a, b; cin >> a >> b;
		int c = lca(a,b);
		if(c == a) cout << 1 << endl;
		else if(c == b) cout << 2 << endl;
		else cout << 0 << endl;
	}
	
	return 0;
}

三、距离

标签：LCA、Tarjan算法

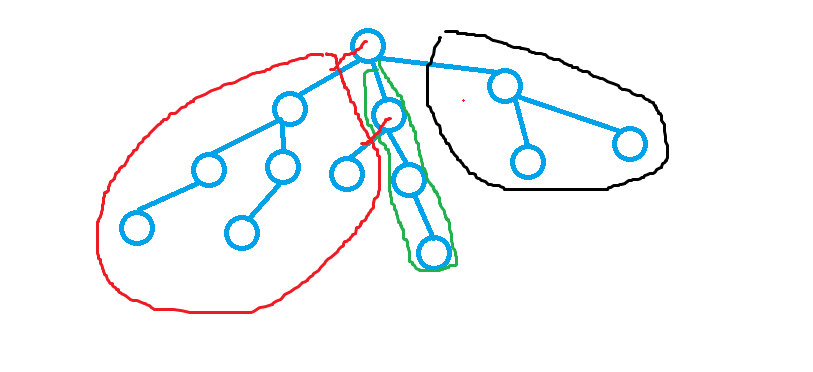
思路：树上两个点只有一条路径，距离就是 $d i s t [a] + d i s t [b] - 2 * d i s t [l c a (a, b)]$ ，其中 $d i s t [i]$ 代表结点 $i$ 到根结点的距离，这个画个图就能想出来了。 $d i s t$ 数组的初始化用深搜或者宽搜都能求出来，最重要的是求 $a, b$ 的最近公共祖先，倍增法我就不讲了，我如下有倍增法的代码，看看就行了，然后这里主要去讲 $T a r jan$ 算法的思路。首先该算法将点分为三种，分别为还未搜索过的、正在搜索的、已经搜索过并且回溯了的，回溯过了的我们用并查集将其与父亲结点合并到一个集合里，如下图所示。我们求的时候是求正在搜索过的点中，有没有询问是与之相关的并且已经搜索过且回溯了的，如果有那么这两个点的最近公共祖先就是已经回溯过的点的在并查集里的根结点，然后用公式求出来即可，更多细节见代码。
在这里插入图片描述

题目描述：

给出 n 个点的一棵树，多次询问两点之间的最短距离。

注意：

边是无向的。所有节点的编号是 1,2,…,n。

输入格式
第一行为两个整数 n 和 m。
n 表示点数，m 表示询问次数；
下来 n−1 行，每行三个整数 x,y,k，表示点 x 和点 y 之间存在一条边长度为 k；
再接下来 m 行，每行两个整数 x,y，表示询问点 x 到点 y 的最短距离。
树中结点编号从 1 到 n。

输出格式
共 m 行，对于每次询问，输出一行询问结果。

数据范围
2≤n≤104,1≤m≤2×104,0<k≤100,1≤x,y≤n
输入样例1：
2 2 
1 2 100 
1 2 
2 1
输出样例1：
100
100
输入样例2：
3 2
1 2 10
3 1 15
1 2
3 2
输出样例2：
10
25

示例代码1：倍增法

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 4e4+10, M = N * 2, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int depth[N], fa[N][16], dist[N];
bool has_father[N];
int root = 1;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void bfs1()
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;

    queue<int> q; q.push(root);
    while(q.size())
    {
        int t = q.front(); q.pop();

        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q.push(j);
                fa[j][0] = t;
                for(int k = 1; k <= 15; ++k)
                {
                    fa[j][k] = fa[fa[j][k-1]][k-1];
                }
            }
        }
    }
}

void bfs2()
{
    memset(dist, 0x3f, sizeof dist);
    dist[root] = 0;

    queue<int> q; q.push(root);
    while(q.size())
    {
        int t = q.front(); q.pop();

        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                q.push(j);
            }
        }
    }
}

int lca(int a, int b)
{
    if(depth[a] < depth[b]) swap(a,b);
    for(int k = 15; k >= 0; --k)
    {
        if(depth[fa[a][k]] >= depth[b])
        {
            a = fa[a][k];
        }
    }
    if(a == b) return a;
    for(int k = 15; k >= 0; --k)
    {
        if(fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    }
    return fa[a][0];
}

int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 0; i < n - 1; ++i)
    {
        int a, b, c; cin >> a >> b >> c;
        add(a,b,c), add(b,a,c);
    }

    bfs1();
    bfs2();

    while(m--)
    {
        int a, b; cin >> a >> b;
        int c = lca(a,b);
        int res = dist[a] + dist[b] - 2 * dist[c];
        cout << res << endl;
    }

    return 0;
}

示例代码2：Tarjan算法

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 1e4+10, M = N * 2, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
int p[N], res[M];
int st[N];
vector<PII> query[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int fa)
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == fa) continue;
        dist[j] = dist[u] + w[i];
        dfs(j,u);
    }
}

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void tarjan(int u)
{
    st[u] = 1;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            tarjan(j);
            p[j] = u;
        }
    }

    for(auto item: query[u])
    {
        int y = item.x, id = item.y;
        if(st[y] == 2)
        {
            int anc = find(y);
            res[id] = dist[u] + dist[y] - dist[anc] * 2;
        }
    }

    st[u] = 2;
}

int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 0; i < n - 1; ++i)
    {
        int a, b, c; cin >> a >> b >> c;
        add(a,b,c), add(b,a,c);
    }

    for(int i = 0; i < m; ++i)
    {
        int a ,b; cin >> a >> b;
        if(a != b)
        {
            query[a].push_back({b,i});
            query[b].push_back({a,i});
        }
    }

    for(int i = 1; i <= n; ++i) p[i] = i;

    dfs(1,-1);
    tarjan(1);

    for(int i = 0; i < m; ++i) cout << res[i] << endl;

    return 0;
}

lijiachang030718

关注

17
点赞
踩
22

收藏

觉得还不错? 一键收藏
打赏
0
评论
算法学习系列（六十二）：LCA（最近公共祖先）：倍增法、Tarjan算法

关于这个 $LCA$ 问题蓝桥杯这两年考的是也是越来越多了，尤其是去年直接出了个裸题（模板题），也是没想到的，再加上今年省赛 $java$ 组也出了一道与之相关的题，所以今年国赛感觉出的几率也是有的。学下来发现其实也没那么难，又是自己想神秘了，思路和代码总的来说都不是很难，难的是想法，这道题你能否能想到用 $LCA$ 做才是关键，所以本章内容还是采用讲题的策略来进行讲解，就其实都是非常经典的问题，几乎都是模板题，但是我觉得蓝桥杯应该不会出特别难的了，因为本身这个算法就很难，还是要多写写熟即可，继续加油吧！
复制链接

扫一扫