七、中间代码与程序分析，《编译原理》（本科教学版），第2版

---

一、中间代码的地位和作用

为什么要用中间表示，中间表示的好处？

编译器的前端，经过一系列的工作后，输出了中间表示，看起来很繁琐。

1.1 最简单的结构

最简单的结构可以直接根据抽象语法树经过翻译，得到汇编。

在这种情况下，中间表示只有一种：抽象语法树

1.2 中间端和后端

我们看更一般的情况，现代编译器的结构

• 抽象语法树经过翻译，中间表示……该过程可以进行很多步
• 得到汇编

1.3 中间代码

• 树和有向无环图(DAG)
  • 高层表示，适用于程序源代码
• 三地址码（3-address code）
  • 低层表示，靠近目标机器
• 控制流图（CFG）
  • 更精细的三地址码，程序的图状表示、
  • 适合做程序分析等
• 静态单赋值形式（SAA）
  • 更精细的控制流图
  • 同时编码控制流信息和数据流信息
• 连续传递风格（CPS）
  • 更一般的SSA
• ……

1.4 为什么要划分成不同的中间表示

• 编译器工程上的考虑
  • 阶段划分：把整个编译过程划分成不同的阶段
  • **任务分解：**每个阶段只处理翻译过程中的一个步骤
  • **代码工程：**代码更容易实现、出错、维护和演进
• 程序分析和代码优化的需要
  • 两者都和程序的中间表示密切相关
    • 许多优化在特定的中间表示上才可以或才容易进行

1.5 通用编译器语言？

为什么人们一直在期待一种通用的编译器语言？

假如我们有n种源语言，m种目标机器语言，那么我们要写 n*m 个编译器

如果我们能够将高级语言都翻译成相同的 IR 这种通用编译器语言，那么我们只需要写 n + m 个编译器

可见，研究编译器语言是非常重要的。

很可惜，现在还没有这样一种 IR，现在只能做到将部分源语言，翻译成同一种中间表示（gcc的做法）

下面将全面讨论中间表示涉及的重要问题和解决方案

• 详细介绍现代编译器中几种常用的重要中间表示
  • 三地址码
  • 控制流图
  • 静态单赋值形式
• 详细介绍在中间表示上做程序分析的理论和技术
  • 控制流分析
  • 数据流分析

二、中间表示：三地址码

2.1 三地址码基本思想

• 给每个中间变量和计算结果命名
  • 没有复合表达式
• 只有最基本的控制流
  • 没有各种控制结构
    • 如if、while、do-while、for
  • 只有goto，call等
• 所以三地址码可以看成是抽象的指令集
  • 通用的RISC

示例

a = 3 + 4 * 5;

if (x < y) 
	z = 6;
else
	z = 7;

=>

x_1 = 4;
x_2 = 5;
x_3 = x_1 * x_2;
x_4 = 3;
x_5 = x_4 + x_3;
a = x_5;
Cjmp(x < y, L_1, L_2);
L_1:
	z = 6;
	jmp L_3;
L_2:
	z = 7;
	jmp L_3;
L_3:
	...

我们发现三地址码只完成一个动作，不再有复合动作。

2.2 三地址码的定义

三地址码中，一条指令的右侧最多有一个运算符。

• 这也是为什么，前面三地址码只完成一个动作，不再有复合动作。

s -> x = n				// 常数赋值
   | x = y + z			// 二元运算
   | x = θ y			// 一元运算
   | x = y				// 数据移动
   | x[y] = z			// 内存写
   | x = y[v]			// 内存读
   | x = f(x1, ..., xn)		// 函数调用
   | Cjmp(x1, L1, L2)		// 条件跳转
   | jmp L					// 无条件跳转	
   | Label L				// 标号
   | Return x				// 函数返回

2.3 如何定义三地址码数据结构？

enum instr_kind {INSERT_CONST, INSTR_MOVE, ...};
struct Instr_t{enum instr_kind kind;};
struct Instr_Add {
    enum instr_kind kind;
    char *x;
    char *y;
    char *z;
};
struct Instr_Move{
	...;
};

2.4 从C–生成三地址码

P -> F*
F -> x((T, id, )*) {(T, id;)* S*}
T -> int
   | bool
S -> x = E
   | printi(E)
   | printb(E)
   | x(E1, ..., En)
   | return E
   | if(E, E*, S*)
   | while(E, S*)
E -> 
   | x
   | true
   | false
   | E + E
   | E && E

需要写如下几个递归函数：

• Gen_P§;
• Gen_F(F);
• Gen_T(T);
• Gen_S(S);
• Gen_E(E);

2.4.1 递归下降代码生成算法：语句的代码生成

Gen_S(S s)
	switch (s)
		case x=e:
			x1 = Gen_E(e);
			emit("x = x1");
			break;
		case printi(e):
			x = Gen_E(e);
			emit("printi(x)");
			break;
		case printb(e):
			x = Gen_E(e);
			emit("printb(x)");
			break;
		case x(e1, ..., en):
			x1 = Gen_E(e1);
			...;
			xn = Gen_E(en);
			emit("x(x1, ..., xn)");
			break;
		case return e:
			x = Gen_E(e);
			emit("return x");
			break;
		case if(e, s1, s2):
			x = Gen_E(e);
			emit("Cjmp(x, L1, L2)");
			emit("Label L1:");
			Gen_SList(s1);
			emit("jmp L3");
			emit("Label L2:");
			Gen_SList(s2);
			emit("jmp L3");
			emit("Label L3:");
			break;
		case while(e, s):
			emit("Label L1:");
			x = Gen_E(e);
			emit("Cjmp(x, L2, L3)");
			emit("Label L2:");
			Gen_SList(s);
			emit("jmp L1");
			emit("Label L3:");
			break;

• if 和 while 的逻辑类似

2.5 小结

• 三地址码的优点：
  • 所有的操作是原子的
    • 变量！没有复合结构
  • 控制流结构被简化了
    • 只有跳转
  • 是抽象的机器代码
    • 向后做代码生成更容易
• 三地址码的不足：
  • 程序的控制流信息是隐式的：谁可以跳转到谁不是很明显
  • 可以做进一步的控制流分析

三、中间表示：控制流图

3.1 三地址码的不足

• 上图给出了一种结构，即控制流图作为三地址码之后的中间表示
• 但是：不同的编译器的中间表示是不同的，所以上图只是一种方式，并非所有的控制流图都要在三地址码后面

三地址码的不足：

• 控制信息是隐式的
• 比如，我们怎样知道有多少条指令会跳转到L_2？我们不得不顺序扫描所有代码

但是如果我们换成如下的控制结构

我们发现只需要看L_2的入度即可

• 程序的控制流图表示带来很多好处：
  • 控制流分析：
    • 对很多程序分析来说，程序的内部结构很重要
      • 典型的问题：“程序中是否存在循环?“
  • 可以进一步进行其他分析：
    • 例如数据流分析
      • 典型的问题：”程序第5行的变量x可能的值是什么？“
• 现代编译器的早期阶段就会倾向做控制流分析
  • 方便后续阶段的分析

3.2 基本概念

• **基本块：**是语句的一个序列，从第一条执行到最后一条
  • 不能从中间进入
  • 不能从中间退出
    • 即跳转指令只能出现在最后
• **控制流图：**控制流图是一个有向图G=(V, E)
  • 节点V：是基本块
  • 边E：是基本块之间的跳转关系

示例

3.2.1 控制流图的定义

// 更为精细的三地址码
S -> x = n
   | x = y + z
   | x = y
   | x = f(x1, x2, ..., xn)
J -> jmp L
   | cjmp(x, L1, L2)
   | return x
B -> Label L;
	S1; S2; ...; Sn
	J
F -> x() { B1, ..., Bn}
P -> F1, ..., Fn

• 一个基本块要有n + 2个要素：
  • 1个名字，n个语句，1个跳转

数据结构定义

struct Block{
    Label_t label;
    List_t stms;
    Jump_t j;
};

3.3 如何生成控制流图

• 可以直接从抽象语法树生成：
  • 如果高层语言具有特别规整控制流结构的话较容易
• 也可以先生成三地址码，然后继续生成控制流图：
  • 对于像C这样的语言更合适
    • 包含像goto这样的非结构化的控制流语句
  • 更加通用（阶段划分！）
• 接下来，我们重点讨论第二种

3.4 由三地址码生成控制流图算法

List_t stms;	// 三地址码中所有语句
List_t blocks = {};		// 控制流图中的所有基本块
Block_t b = block_fresh();
scan_stms() {
	foreach(s ∈ stms) {
		if (s is "Label L")		// s 是标号
			b.Label = L;
         else (s is some jump)		// s 是跳转
         	b.j = s;
         	blocks ∪= {b};
         	b = Block_fresh();		
         else					// s 是普通指令
         	b.stms ∪= {s};
	}
}

时间复杂度：O(N)

3.5 控制流图的基本操作

• 标准的图论算法都可以用在控制流图的操作上：
  • 各种遍历算法、生成树、必经节点结构、等等
• 图节点的顺序有重要的应用：
  • 拓扑序、逆拓扑序、近似拓扑序、等等
• 下面通过研究一个具体的例子来展示基本图算法的应用：
  • 死基本块删除优化

3.6 死基本块删除优化的示例

• L3 的入度为0并且走不到，可以删除

四、中间表示：数据流分析

数据流分析往往和优化绑定在一起。

• 值得说明的一点是，优化不仅仅在中间表示阶段发生，现代编译器很激进，也可以在抽象语法树、汇编层面来进行优化。

4.1 优化的一般模式

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

• 程序分析
  • 控制流分析，数据流分析，依赖分析
  • 得到被优化程序的静态保守信息
    • 是对动态运行行为的近似
• 程序重写
  • 以上一步得到的信息制导对程序的重写

4.2 静态保守

上面是一个有四个基本块的控制流图.

问题:

• 能把y替换成3吗?如果能, 这称为**“常量传播”**优化

对程序进行分析的结果表明:只有L_0块中的y=3能到达L_3。这种分析称为**“到达定义”**分析。

假如我们改写上面的代码:

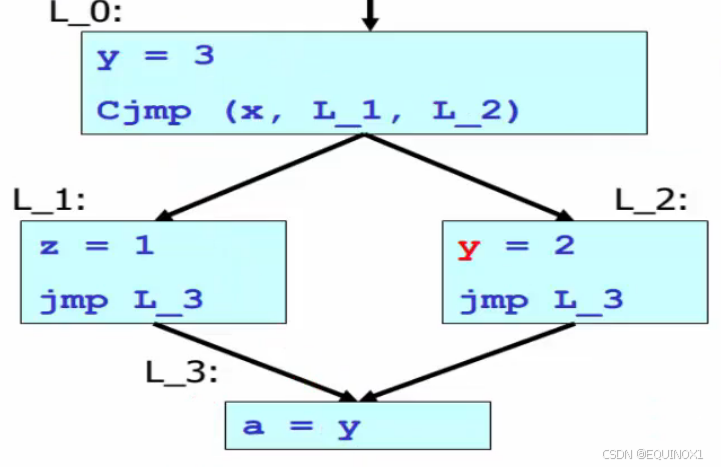
问题:

• 能把y替换成3吗?如果能, 这称为**“常量传播”**优化
• 编译器需要判断 x 是否始终是true
• 但若x是程序输入的话，运行时才能知道值。所以编译器只能采用静态能够获得的信息对程序做保守估计: “L2可能会执行”

小结一下:

• 通过对程序代码进行静态分析，得到关于程序数据相关的保守信息
  • 必须保证程序分析的结果是安全的
• 根据优化的目标不同，·雪要进行的数据流分析也不同
  • 接下来我们将研究两种具体的数据流分析
    • 到达定义分析
    • 活性分析

4.3 到达定义分析

4.3.1 定义、使用

定义（def）：对变量的赋值

• y = 3

使用（use）：对变量值的读取

需要回答的问题：有哪些对变量 y 的定义能够到达语句7

• 语句1

到达定义：对每个变量的使用点，有哪些定义可以到达？（即：该变量的值是在哪赋值的？）

• 如果说变量的定义为常数，并且可以到达的使用点只有一个，那么就可以常量传播优化

4.3.2 数据流方程

对任何一条定义：

• [d: x = …]

给出两个集合：

• gen[d: x= …] = { d }
  • gen 为产生定义的标号集合
  • 如 gen[1: x = 1] = { 1 }
• kill [d: x = …] = defs[x] - {d}
  • defs[x] 为 x 的所有定义点集合
  • defs[x] - {d}，亦即，除了自身，其他所有的定义点都会被当前这个定义点杀死，因为后面紧接着的语句只会见到自己

数据流方程：

• $in[s_i]=out[s_{i-1}]$
• $out[s_i]=gen[s_i]\cup (in[s_i]-kill[s_i])$

$in[s_i]$: 能够到达 $s_i$ 的定义集合

$out[s_i]$: 能够从 $s_i$ 出去的定义集合

4.3.3 从数据流方程到算法

算法：对一个基本块的到达定义算法

输入：基本块中所有的语句

输出：对每个语句计算 in 和 out 两个集合

List_t stms;			// 一个基本块中所有语句
set = {};				// 临时变量，记录当前语句s的in集合
reaching_defination ()
	foreach (s ∈ stms)
		in[s] = set;
		out[s] = gen[s] ∪ (in[s] - kill[s])
		set = out[s]

算法非常简单，不再赘述

4.3.4 对于一般的控制流图

对于一般的控制流图，一个节点的会有多个前驱节点：

• 前向数据流方程：
  • $in[s]={\cup }_{p\in pred(s)}out[p]$
  • $out[s]=gen[s]\cup (in[s]-kill[s])$

4.3.5 从数据流方程到不动点算法

算法：对所有基本块的到达定义算法

输入：基本块中所有的语句

输出：对每个语句计算 in 和 out 两个集合

List_t stms;			// 所有基本块中所有语句
set = {};				// 临时变量，记录当前语句s的in集合
reaching_defination ()
	while (some set in[] or out[] is still changing)
		foreach (s ∈ stms)
			set ∪= out[p];
		in[s] = set;
		out[s] = gen[s] ∪ (in[s] - kill[s]);

示例：

对于为什么一定能够找到不动点，程序终止，这里不做讨论。

五、中间表示：活性分析

5.1 进行活性分析的动机

• 在代码生成的讨论中，我们曾假设目标机器有无限多个(虚拟)寄存器可用
  • 简化了代码生成的算法
  • 对物理机器是个坏消息
    • 机器只有有限多个寄存器
      • 必须把无限多个虚拟寄存器分配到有限个寄存器中
• 这是寄存器分配优化的任务
  • 需要进行活性分析

示例

考虑这段三地址码：

a = 1
b = a + 2
c = b + 3
return c

• 有三个变量a，b，c

• 假设目标机器上只有一个物理寄存器：r

• 是否可能把三个变量a，b，c同时放到寄存器r中?

• 我们自然不能同时把 a，b，c放入r中，但是上述程序中我们显然可以利用一个寄存器r 得出结果c

• 三个变量分阶段，交替使用 r 即可

引出的问题：计算在给定的程序点，哪些变量是”活跃“的

• **活跃：**占用寄存器

活跃信息给出了活跃区间的概念。

活跃区间互不相交，所以三个变量可交替使用同一个寄存器。

示例

考虑这段三地址码

a = 1		   寄存器分配:			
b = a + 2		a => r
c = b + 3		b => r
return c		c => r

代码重写：

r = 1
r = r + 2
r = r + 3
return r

5.2 数据流方程

对任何一条语句：

[d: s]

给出两个集合：

• use[d: s] = { x | 变量x在语句s中被使用 }
• def[d: s] = { x | 变量x在语句s中被定义 }

比如：

1: x = y + z
2: z = z + x
use[1] = {y, z}
def[1] = {x}

基本块内的后向数据流方程：

• $out[s_i]=in[s_{i+1}]$
• $in[s_i]=use[s_i]\cup (out[s_i]-def[s_i])$

根据这样的后向数据流方程，我们可以倒推出每一条语句的活跃变量

如示例中的程序，我们可以做出如下推导：
o u t = ∅ 1 、 a = 1          i n = ∅ o u t = { a } 2 、 b = a + 2          i n = a o u t = { b } 3 、 c = b + 3          i n = { b } o u t = { c } 4 、 r e t u r n   c         i n = { c } o u t = ∅ \begin{align} & out=\empty \\ & 1、a = 1 \ \ \ \ \ \ \ \ in = \empty \\ & out=\{a\} \\ & 2、b = a + 2 \ \ \ \ \ \ \ \ in= {a} \\ & out=\{b\} \\ & 3、c = b + 3 \ \ \ \ \ \ \ \ in=\{b\} \\ & out=\{c\} \\ & 4、return \ c \ \ \ \ \ \ \ in=\{c\}\\ & out=\empty \end{align} ​out=∅1、a=1        in=∅out={a}2、b=a+2        in=aout={b}3、c=b+3        in={b}out={c}4、return c       in={c}out=∅​​
再给一个示例：

out = {}
a = 1    	in = {}					c     b          a
out = {a}						    	 		    |
b = a + 2 	in = {a}					 			|
out = {a, b}						      | 		|
c = b + 3	in = {a, b}					  | 		 |
out = {a, c}						|				|
return a + c		in = {a, c}		 |				 |
out = {}						    |				|

我们发现在上述程序中：

• a 始终活跃
• b、c分别处于两段不相交的活跃区间
• 因而a需要分配一个寄存器，b、c可以交替使用同一个寄存器

5.3 一般的数据流方程

• 方程
  • $out[s]={\cup }_{p\in succ[s]}in[p]$
  • $in[s]=use[s]\cup (out[s]-def[s])$
• 同样可给出不动点算法
  • 从初始的空集{ }出发
  • 循环到没有集合变化为止

5.4 干扰图

• 干扰图是一个无向图G = (V，E)：

  1. 对每个变量构造无向图G中一个节点;
  2. 若变量x，y同时活跃，在x、y间连一条无向边。

• 显然，连边的两个节点不能够共用寄存器

• 这其实就转化为了图论中独立集的问题

• 我们对顶点进行着色，任意两个相连点颜色不同

• 下一章寄存器分配会用到该数据结构，并通过启发式图着色来解决问题