平衡二叉树快速入门

最新推荐文章于 2022-11-15 17:25:08 发布
最新推荐文章于 2022-11-15 17:25:08 发布
阅读量303 收藏
点赞数
分类专栏： 算法和数据结构 文章标签： 数据结构 平衡二叉树 AVL Tree
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ET_Endeavoring/article/details/119900866
版权

定义

 平衡因子

二叉树结点的左子树与右子树的高度(深度)差即为该结点的平衡因子（BF,Balance Factor）。

最小失衡子树

实现方式

 《大话数据结构》里的平衡二叉树是用平衡因子实现的，这种方法效率略高，却实现复杂。《数据结构与算法分析C++》里是用的高度实现的。接下来会分别介绍两种实现方式。

利用平衡因子实现平衡二叉树

这种实现方式复杂的地方在于平衡因子的更新。

节点定义

#define RH -1
#define EH 0
#define LH 1

typedef struct AVLNode {
    int data;
    int bf;                 // 平衡因子
    struct AVLNode *left;   // 左孩子
    struct AVLNode *right;  // 右孩子
}AVLNode, *AVLTree;

左旋和右旋代码

// 旋转以t为根节点的二叉树，最后t指向新的根节点
// 左旋
void rotateLeft(AVLTree *t) {
    AVLTree r = (*t)->right;
    (*t)->right = r->left;
    r->left = (*t);
    (*t) = r;
}
// 右旋
void rotateRight(AVLTree *t) {
    AVLTree l = (*t)->left;
    (*t)->left = l->right;
    l->right = (*t);
    (*t) = l;
}

插入节点

1是LL，2是LR，3是RL，4是RR。

 LL和RR是单旋转，LR和RL是双旋转。

插入流程：

  • 按二叉排序树插入
  • 插入后判断是否平衡
  • 平衡则修改平衡因子
  • 不平衡则判断类型，单旋转还是双旋转，修改平衡因子

  • 递归的弹栈过程从叶子节点往上更新平衡因子，若某节点的平衡因子绝对值大于1时（2或-2），以该节点为根节点的树是一颗最小失衡子树，需要重新平衡。

四种旋转类型配图：

t表示最小失衡子树的根节点

l是t的左孩子，lr是l的右孩子

r是t的右孩子，rl是r的左孩子

注意：本文图片里用橙色标注的t，l，lr，r，rl指的都是旋转前的节点。例如下图旋转前t是3，旋转后t还是3。

LL型

插入节点在最小不平衡子树的根节点的左孩子的左子树上 

直接右旋，3种情况都是一个右旋完事

情况1

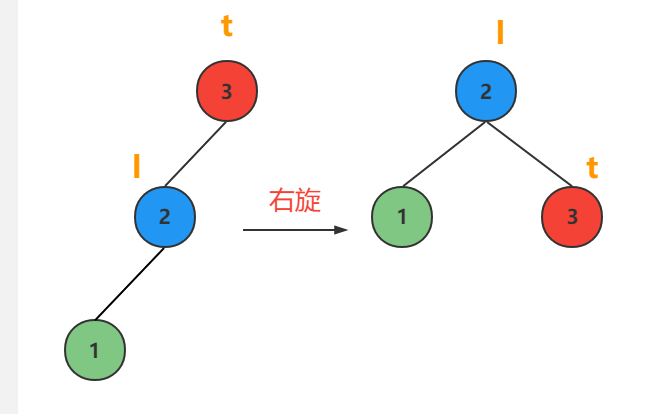
情况2

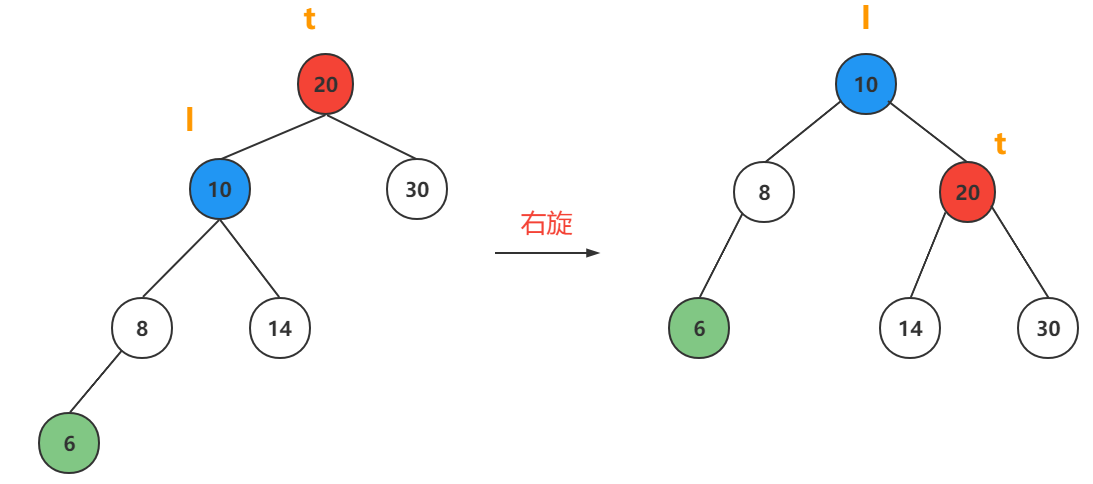
情况3

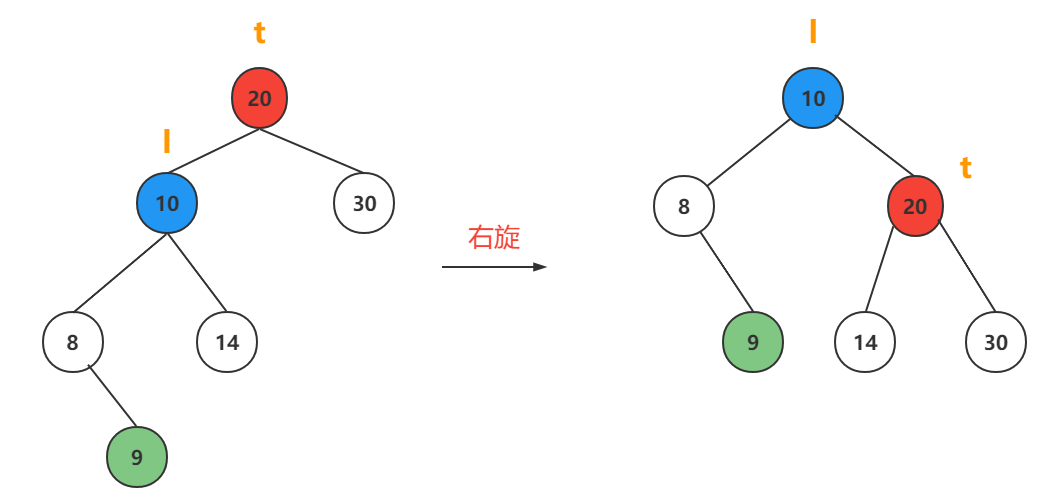
     // LL型
    case LH:
        (*t)->bf = EH;
        l->bf = EH;
        rotateRight(t);
        break;

LR型

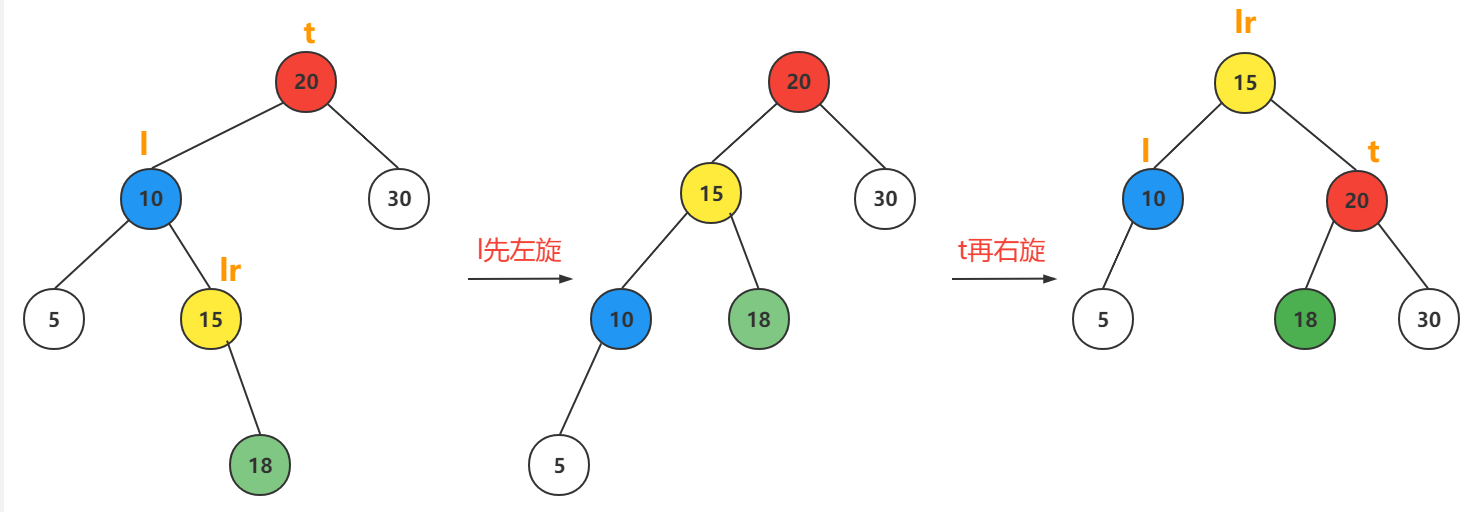
 插入节点在最小不平衡子树的根节点的左孩子的右子树上 

l先左旋，t再右旋

根据lr节点的平衡因子值分为三种情况：

1. lr->bf==0

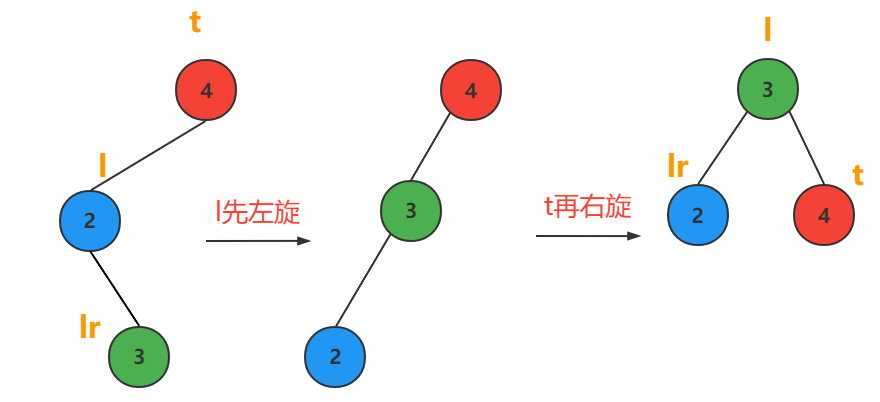
2. lr->bf==1

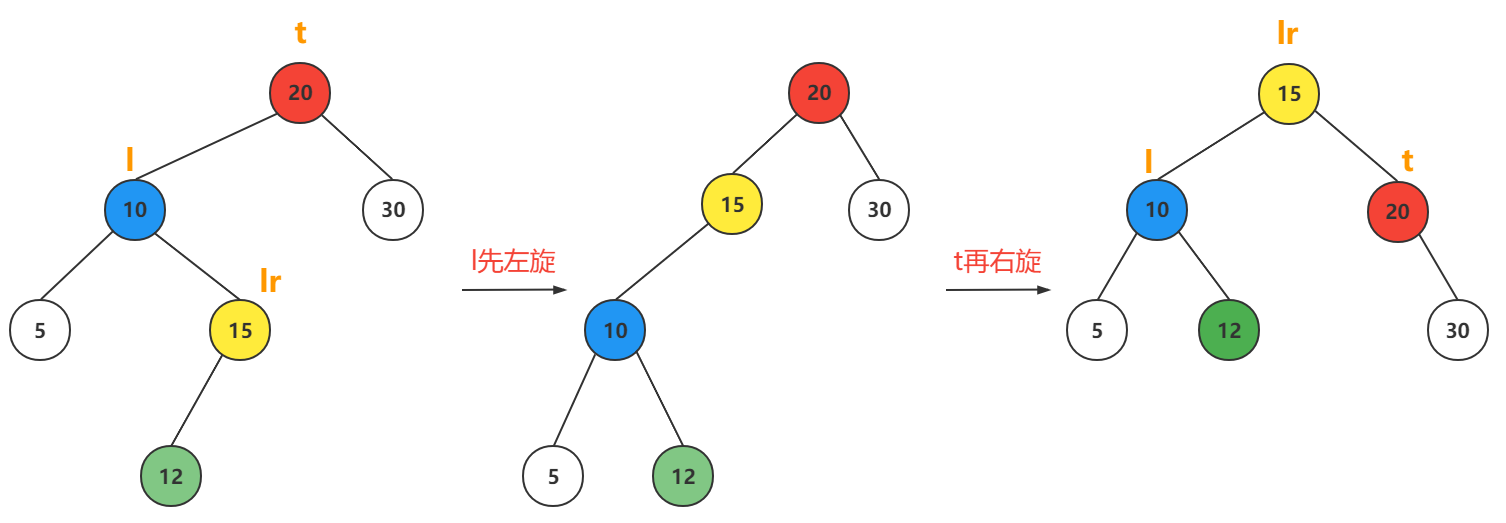
3. lr->bf==-1

 // LR型
    case RH:
        lr = l->right;
        switch (lr->bf)
        {
        case LH:            // 插入节点是lr的左孩子
            (*t)->bf = RH;  // *t右旋失去左孩子，故(*t)->bf变为-1
            l->bf = EH;     // l左旋先失去右孩子，而lr的左孩子（插入节点）又变成l的右孩子，故l->bf仍是0
            break;
        case EH:            // 插入节点是lr
            (*t)->bf = EH;  // *t和r变为叶子节点，故bf都是0
            l->bf = EH; 
            break;
        case RH:            // 插入节点是lr的右孩子
            (*t)->bf = EH;  // *t右旋先失去左孩子，而lr的右孩子（插入节点）又变成*t的左孩子，故(*t)->仍是0
            l->bf = LH;     // l左旋失去右孩子，故l->bf是1
            break;
        default:
            break;
        }

        lr->bf = EH;        // rl上升1层或2层，bf肯定是0

        rotateLeft(&(*t)->left);
        rotateRight(t);
        break;

RR型

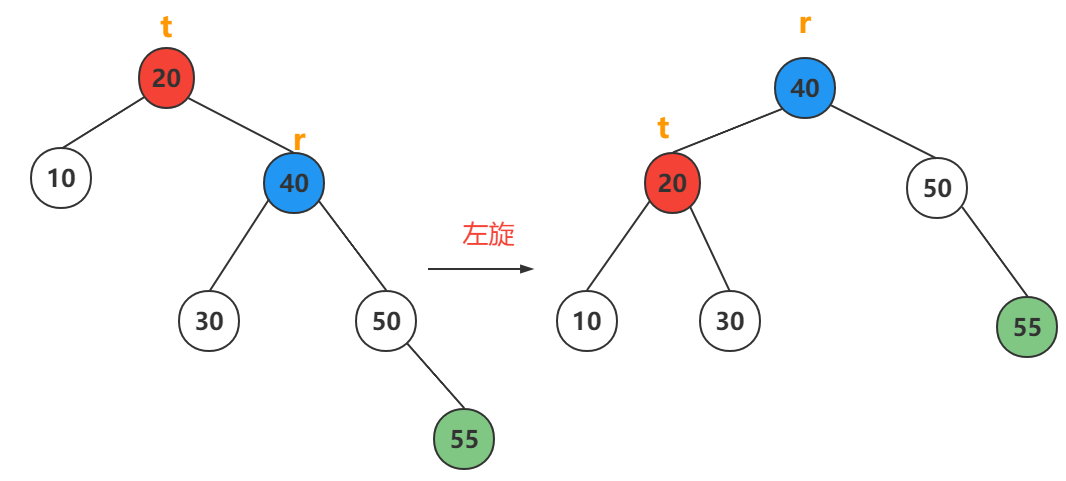
  插入节点在最小不平衡子树的根节点的右孩子的右子树上 

3种情况都是一个左旋完事

情况1 

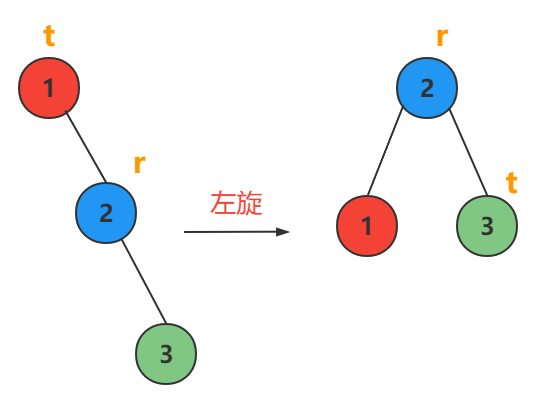
情况2

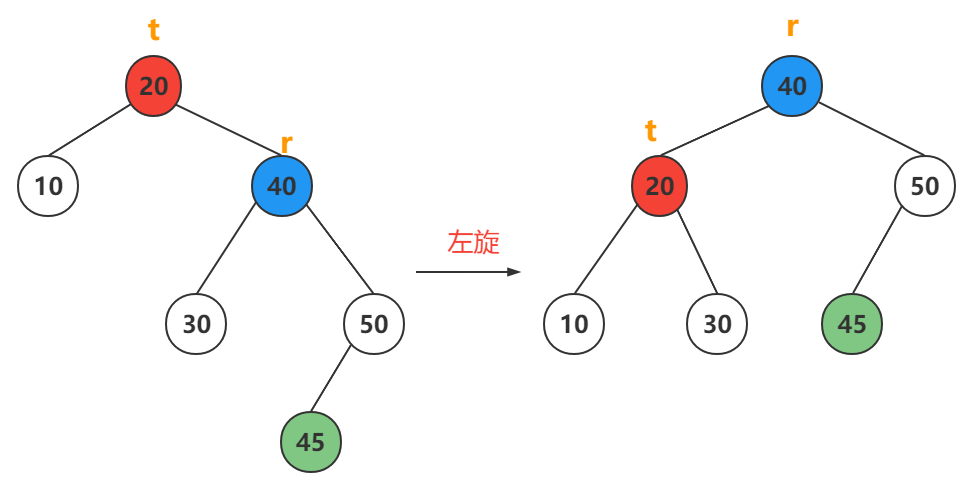
情况3

     // RR型
    case RH:
        (*t)->bf = EH;
        r->bf = EH;
        rotateLeft(t);
        break;

RL型

插入节点在最小不平衡子树的根节点的右孩子的左子树上 

r先右旋，t再左旋

根据rl节点的平衡因子值分为三种情况：

1. lr->bf==0

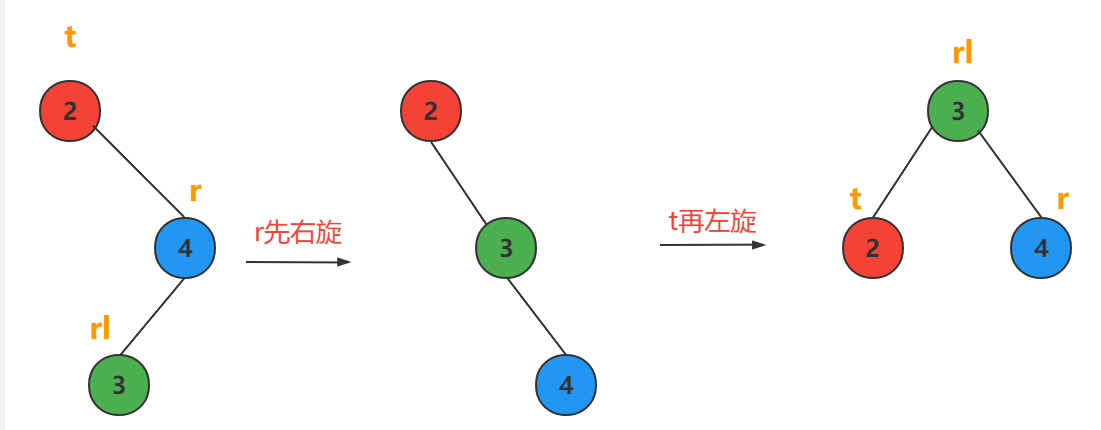
2. lr->bf==1

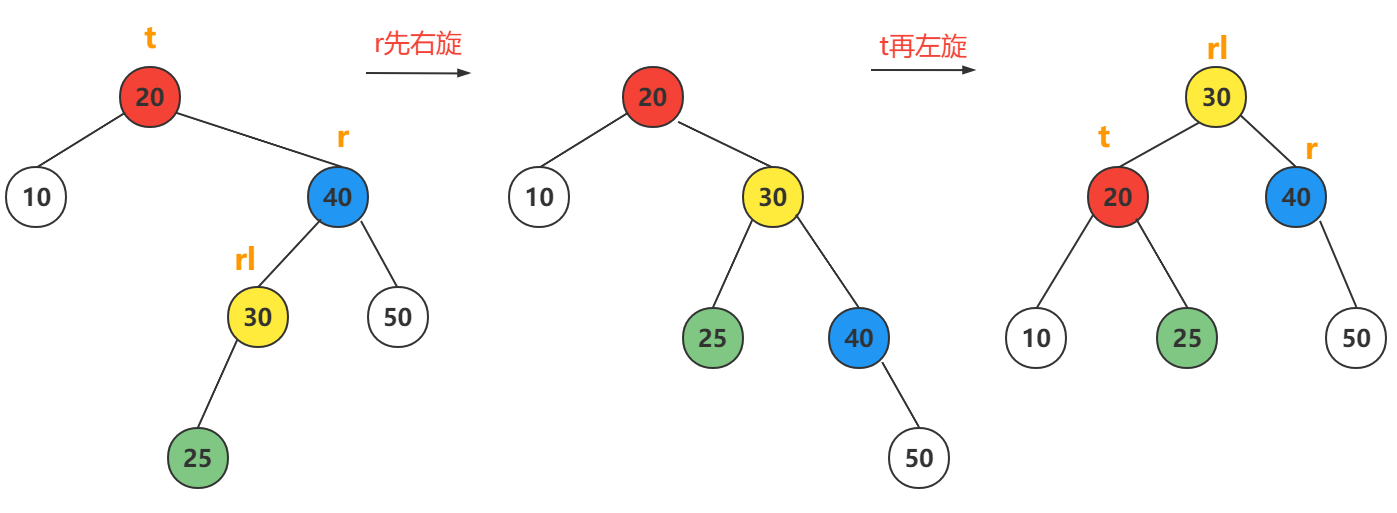
3. lr->bf==-1

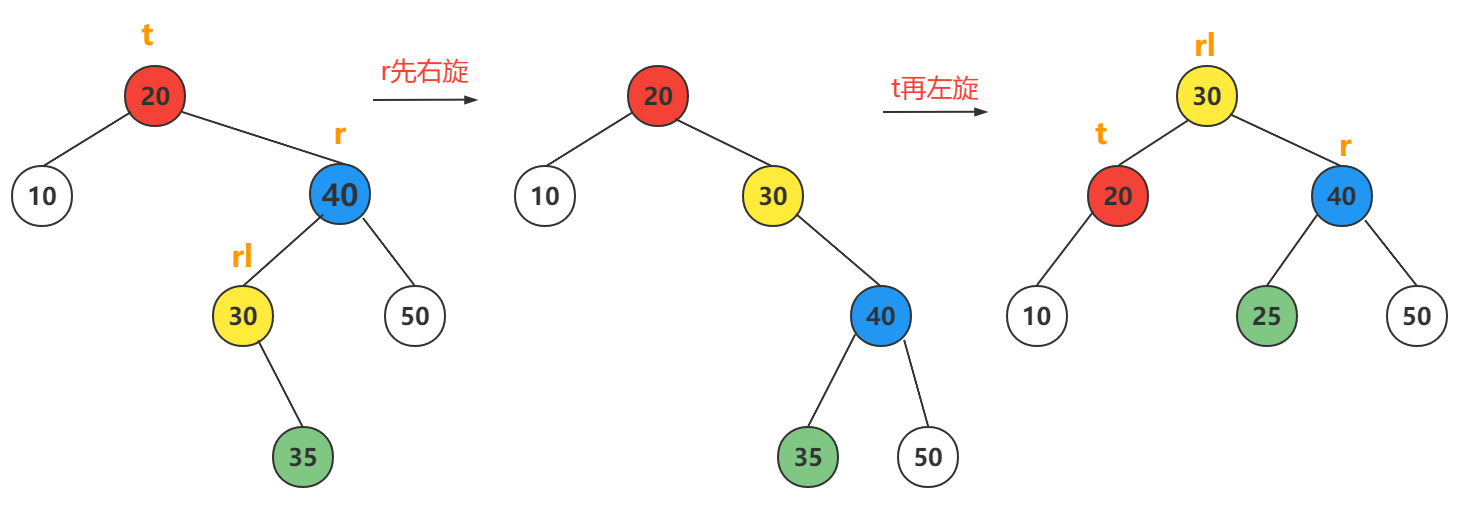
    // RL型
    case LH:
        rl = r->left;
        switch (rl->bf) {
        case RH:
            (*t)->bf = LH;  // (*t)一定有左孩子，左旋后右孩子没了，所以bf是1
            r->bf = EH;     // rl的右孩子变成r的左孩子，故r的bf变为0
            break;
        case EH:
            (*t)->bf = EH;
            r->bf = EH;     // *t和r变为叶子节点，故bf都是0
            break;
        case LH:
            (*t)->bf = EH;  // (*t)一定有左孩子，rl上升两层，rl的左孩子变为(*t)的右孩子，故(*t)->bf是0
            r->bf = RH;     // 右旋，r失去左孩子，故r->bf变为-1
            break;
        default:
            break;
        }
        rl->bf = 0;         // rl上升1层或2层，bf肯定是0

        rotateRight(&(*t)->right);
        rotateLeft(t);
        break;

 插入节点代码：

  • 插入节点前左右子树一样高，插入后某颗子树变高，*isTaller设为1，递归展开（unwinding recursion）时更新上层节点的平衡因子。
  • 插入节点前某颗子树较高，插入节点到另一颗子树，则左右子树一样高，不需要更新上层节点的平衡因子，*isTaller设为0。
  • 插入节点前某颗子树较高，还往这颗子树插入节点，则出现最小不平衡子树，需要平衡，平衡后*isTaller设为0。
int insertAVLTree(AVLTree *t, int data, int *isTaller) {
    if (NULL == *t) {
        *t = (AVLTree)malloc(sizeof(AVLNode));
        (*t)->data = data;
        (*t)->left = (*t)->right = NULL;
        (*t)->bf = EH;
        *isTaller = 1;
        //printf("new data: %d\n", data);
        return 1;
    }

    if (data == (*t)->data) {
        *isTaller = 0;
        return 1;
    }
    else if(data < (*t)->data) {
        insertAVLTree(&(*t)->left, data, isTaller);
        if (*isTaller) {
            switch ((*t)->bf) {
            // 原本右子树高，插入左节点后左右子树一样高
            case RH:
                (*t)->bf = EH;
                *isTaller = 0;
                break;

            // 原本左右子树一样高，插入左节点后左子树高一层
            case EH:
                (*t)->bf = LH;
                (*isTaller) = 1;
                break;

            // 原本左子树高，插入左节点后需要重新平衡
            case LH:
                //printf("balanceLeft\n");
                balanceLeft(t);
                *isTaller = 0;
                break;

            default:
                break;
            }
        }
    }
    else {
        insertAVLTree(&(*t)->right, data, isTaller);
        if (*isTaller) {
            switch ((*t)->bf) {
                // 原本右子树高，插入右节点后需要重新平衡
            case RH:
                //printf("balanceRight\n");
                balanceRight(t);
                *isTaller = 0;
                break;

                // 原本左右子树一样高，插入右节点后右子树高一层
            case EH:
                (*t)->bf = RH;
                *isTaller = 1;
                break;

                // 原本左子树高，插入右节点后左右子树一样高
            case LH:
                (*t)->bf = EH;
                *isTaller = 0;
                break;

            default:
                break;
            }
        }
    }
    return 1;
}

删除节点

先递归查找要删除节点，找到后判断是哪种删除类型。

删除节点主要有4种情况：

1. 删除的是叶子节点

直接释放该节点内存，递归展开的时候判断树是否变矮（这里参考插入代码使用isShorter），如果变矮了，*isShorter仍保持1。如果某个上层节点的平衡因子是0，则*isShorter设为0，这时候已经是平衡的，不需要再更新平衡因子了。如果删除节点导致一边出现不平衡则需要重新平衡，这里复用插入的平衡代码（balanceLeft/balanceRight）,但是比插入多了一种情况：l或r的平衡因子是0。

        if (NULL == (*t)->left && NULL == (*t)->right) {
            free(*t);
            *t = NULL;
        }

2. 删除的节点只有左孩子

将删除节点*t替换成左孩子，释放左孩子内存，*t的平衡因子变为0

        else if (NULL != (*t)->left && NULL == (*t)->right) {
            (*t)->data = (*t)->left->data;
            (*t)->bf = 0;
            free((*t)->left);
            (*t)->left = NULL;
        }

3. 删除的节点只有右孩子

跟情况2对称，将删除节点*t替换成右孩子，释放右孩子内存，*t的平衡因子变为0

        else if (NULL == (*t)->left && NULL != (*t)->right) {
            (*t)->data = (*t)->right->data;
            (*t)->bf = 0;
            free((*t)->right);
            (*t)->right = NULL;
        }

4. 删除的节点既有左孩子又有右孩子

这种情况最复杂，按照二叉排序树 删除逻辑，应该用删除节点的前驱或后继替换删除节点。我的实现里只使用前驱。前驱就是删除节点的左子树中的最大值（位置在最右）。下图要删除42的话，则要先找到它的前驱19，这里我使用了一个辅助函数updateBf，在updateBf里递归找到前驱，由于前驱要替换被删除节点，所以相当于删除了前驱，那么上层节点要相应更新平衡因子。

updateBf实现：

void updateBf(AVLTree *t, int *isShorter, AVLTree *pre) {
    if (NULL != (*t)->right) {
        updateBf(&(*t)->right, isShorter, pre);

        if (*isShorter) {
            switch ((*t)->bf) {
            case LH:
                balanceLeft(t);
                if (EH == (*t)->bf) {
                    *isShorter = 1;
                }
                else {
                    *isShorter = 0;
                }
                break;

            case EH:
                (*t)->bf = LH;
                *isShorter = 0;
                break;

            case RH:
                (*t)->bf = EH;
                *isShorter = 1;
                break;

            default:
                break;
            }
        }
    }
    else {
        *pre = *t;
        // 前驱的左孩子
        (*t) = (*t)->left;
    }
}

 在updateBf外层可能还需要更新平衡因子：
 

        else {
            // 前驱
            AVLTree pre = NULL;
            updateBf(&(*t)->left, isShorter, &pre);

            (*t)->data = pre->data;
            free(pre);

            if (*isShorter) {
                switch ((*t)->bf)
                {
                case LH:
                    (*t)->bf = EH;
                    *isShorter = 1;
                    break;

                case EH:
                    (*t)->bf = RH;
                    *isShorter = 0;
                    break;

                case RH:
                    balanceRight(t);

                    if (EH == (*t)->bf) {
                        // 平衡后高度-1
                        *isShorter = 1;
                    }
                    else {
                        *isShorter = 0;
                    }
                    break;

                default:
                    break;
                }
            }
        }

可以看到第4种情况实现较复杂。

完整代码

#include <stdio.h>
#include <malloc.h>

#define NodeNum 20

#define RH -1
#define EH 0
#define LH 1

typedef struct AVLNode {
    int data;
    int bf;                 // 平衡因子
    struct AVLNode *left;   // 左孩子
    struct AVLNode *right;  // 右孩子
}AVLNode, *AVLTree;

// 旋转以t为根节点的二叉树，最后t指向新的根节点
// 左旋
void rotateLeft(AVLTree *t) {
    AVLTree r = (*t)->right;
    (*t)->right = r->left;
    r->left = (*t);
    (*t) = r;
}
// 右旋
void rotateRight(AVLTree *t) {
    AVLTree l = (*t)->left;
    (*t)->left = l->right;
    l->right = (*t);
    (*t) = l;
}

// 平衡左子树
void balanceLeft(AVLTree *t) {
    AVLTree l = (*t)->left;
    AVLTree lr;
    switch (l->bf) {
     // LL型
    case LH:
        (*t)->bf = EH;
        l->bf = EH;
        rotateRight(t);
        break;

    // LR型
    case RH:
        lr = l->right;
        switch (lr->bf)
        {
        case LH:            // 插入节点是lr的左孩子
            (*t)->bf = RH;  // *t右旋失去左孩子，故(*t)->bf变为-1
            l->bf = EH;     // l左旋先失去右孩子，而lr的左孩子（插入节点）又变成l的右孩子，故l->bf仍是0
            break;
        case EH:            // 插入节点是lr
            (*t)->bf = EH;  // *t和r变为叶子节点，故bf都是0
            l->bf = EH; 
            break;
        case RH:            // 插入节点是lr的右孩子
            (*t)->bf = EH;  // *t右旋先失去左孩子，而lr的右孩子（插入节点）又变成*t的左孩子，故(*t)->仍是0
            l->bf = LH;     // l左旋失去右孩子，故l->bf是1
            break;
        default:
            break;
        }

        lr->bf = EH;        // rl上升1层或2层，bf肯定是0

        rotateLeft(&(*t)->left);
        rotateRight(t);
        break;

    // 删除的时候才用到
    case EH:
        rotateRight(t);
        // l->bf==0比l->bf==1时右子树高一层，故平衡后t的bf变为-1
        // 平衡前的l的bf平衡后不变
        (*t)->bf = RH;
        break;

    default:
        break;
    }
}

// 平衡右子树
void balanceRight(AVLTree *t) {
    AVLTree r = (*t)->right;
    AVLTree rl;
    switch (r->bf) {
     // RR型
    case RH:
        (*t)->bf = EH;
        r->bf = EH;
        rotateLeft(t);
        break;

    // RL型
    case LH:
        rl = r->left;
        switch (rl->bf) {
        case RH:
            (*t)->bf = LH;  // (*t)一定有左孩子，左旋后右孩子没了，所以bf是1
            r->bf = EH;     // rl的右孩子变成r的左孩子，故r的bf变为0
            break;
        case EH:
            (*t)->bf = EH;
            r->bf = EH;     // *t和r变为叶子节点，故bf都是0
            break;
        case LH:
            (*t)->bf = EH;  // (*t)一定有左孩子，rl上升两层，rl的左孩子变为(*t)的右孩子，故(*t)->bf是0
            r->bf = RH;     // 右旋，r失去左孩子，故r->bf变为-1
            break;
        default:
            break;
        }
        rl->bf = 0;         // rl上升1层或2层，bf肯定是0

        rotateRight(&(*t)->right);
        rotateLeft(t);
        break;

    // 删除的时候才用到
    case EH:
        rotateLeft(t);
        // r->bf==0比r->bf==1时左子树高一层，故平衡后t的bf变为1
        // r->bf和平衡前一样
        (*t)->bf = LH;
        break;

    default:
        break;
    }
}

int insertAVLTree(AVLTree *t, int data, int *isTaller) {
    if (NULL == *t) {
        *t = (AVLTree)malloc(sizeof(AVLNode));
        (*t)->data = data;
        (*t)->left = (*t)->right = NULL;
        (*t)->bf = EH;
        *isTaller = 1;
        //printf("new data: %d\n", data);
        return 1;
    }

    if (data == (*t)->data) {
        *isTaller = 0;
        return 1;
    }
    else if(data < (*t)->data) {
        insertAVLTree(&(*t)->left, data, isTaller);
        if (*isTaller) {
            switch ((*t)->bf) {
            // 原本右子树高，插入左节点后左右子树一样高
            case RH:
                (*t)->bf = EH;
                *isTaller = 0;
                break;

            // 原本左右子树一样高，插入左节点后左子树高一层
            case EH:
                (*t)->bf = LH;
                (*isTaller) = 1;
                break;

            // 原本左子树高，插入左节点后需要重新平衡
            case LH:
                //printf("balanceLeft\n");
                balanceLeft(t);
                *isTaller = 0;
                break;

            default:
                break;
            }
        }
    }
    else {
        insertAVLTree(&(*t)->right, data, isTaller);
        if (*isTaller) {
            switch ((*t)->bf) {
                // 原本右子树高，插入右节点后需要重新平衡
            case RH:
                //printf("balanceRight\n");
                balanceRight(t);
                *isTaller = 0;
                break;

                // 原本左右子树一样高，插入右节点后右子树高一层
            case EH:
                (*t)->bf = RH;
                *isTaller = 1;
                break;

                // 原本左子树高，插入右节点后左右子树一样高
            case LH:
                (*t)->bf = EH;
                *isTaller = 0;
                break;

            default:
                break;
            }
        }
    }
    return 1;
}

void updateBf(AVLTree *t, int *isShorter, AVLTree *pre) {
    if (NULL != (*t)->right) {
        updateBf(&(*t)->right, isShorter, pre);

        if (*isShorter) {
            switch ((*t)->bf) {
            case LH:
                balanceLeft(t);
                if (EH == (*t)->bf) {
                    *isShorter = 1;
                }
                else {
                    *isShorter = 0;
                }
                break;

            case EH:
                (*t)->bf = LH;
                *isShorter = 0;
                break;

            case RH:
                (*t)->bf = EH;
                *isShorter = 1;
                break;

            default:
                break;
            }
        }
    }
    else {
        *pre = *t;
        // 前驱的左孩子
        (*t) = (*t)->left;
    }
}

void deleteAVLTree(AVLTree *t, int data, int *isShorter) {
    if (NULL == t || NULL == *t) {
        return;
    }
    if (data < (*t)->data) {
        deleteAVLTree(&(*t)->left, data, isShorter);

        if (*isShorter) {
            switch ((*t)->bf)
            {
            case LH:
                (*t)->bf = EH;
                *isShorter = 1;
                break;

            case EH:
                (*t)->bf = RH;
                *isShorter = 0;
                break;

            case RH:
                balanceRight(t);

                if (EH == (*t)->bf) {
                    // 平衡后高度-1
                    *isShorter = 1;
                }
                else {
                    // l有右孩子
                    *isShorter = 0;
                }
                break;

            default:
                break;
            }
        }
    }
    else if (data > (*t)->data) {
        deleteAVLTree(&(*t)->right, data, isShorter);

        if (*isShorter) {
            switch ((*t)->bf)
            {
            case LH:

                balanceLeft(t);

                if (EH == (*t)->bf) {
                    *isShorter = 1;
                }
                else {
                    // r有左孩子
                    *isShorter = 0;
                }
                break;

            case EH:
                (*t)->bf = LH;
                *isShorter = 0;
                break;

            case RH:
                (*t)->bf = EH;
                *isShorter = 1;
                break;

            default:
                break;
            }
        }
    }
    else {
        *isShorter = 1;

        if (NULL == (*t)->left && NULL == (*t)->right) {
            free(*t);
            *t = NULL;
        }
        else if (NULL != (*t)->left && NULL == (*t)->right) {
            (*t)->data = (*t)->left->data;
            (*t)->bf = 0;
            free((*t)->left);
            (*t)->left = NULL;
        }
        else if (NULL == (*t)->left && NULL != (*t)->right) {
            (*t)->data = (*t)->right->data;
            (*t)->bf = 0;
            free((*t)->right);
            (*t)->right = NULL;
        }
        else {
            // 前驱
            AVLTree pre = NULL;
            updateBf(&(*t)->left, isShorter, &pre);

            (*t)->data = pre->data;
            free(pre);

            if (*isShorter) {
                switch ((*t)->bf)
                {
                case LH:
                    (*t)->bf = EH;
                    *isShorter = 1;
                    break;

                case EH:
                    (*t)->bf = RH;
                    *isShorter = 0;
                    break;

                case RH:
                    balanceRight(t);

                    if (EH == (*t)->bf) {
                        // 平衡后高度-1
                        *isShorter = 1;
                    }
                    else {
                        *isShorter = 0;
                    }
                    break;

                default:
                    break;
                }
            }
        }
    }
}

void traversal(AVLTree t) {
    if (NULL == t) {
        return;
    }
    traversal(t->left);
    printf("%d bf:%d\n", t->data, t->bf);
    traversal(t->right);
}

int main() {
#if 0
    int a[] = { 13,42,61,75,15,6,58,160,19,7 };
    int b[] = { 58,61,75,13,6,160,19,42,7,15 };
#elif 0
    int a[] = { 50,11,32,72,99,41,65,29,20,91 };
    int b[] = { 29,11,99,91,32,41,50,65,20,72 };
#elif 0
    int a[] = { 77, 66, 55, 33, 99, 22, 11, 44, 88, 100 };
    int b[] = { 44,77, 66, 55, 99, 22, 11, 88, 100, 33};
#elif 1
    int a[] = { 42, 61, 96, 43, 36, 31, 45, 87, 6, 41,
        92, 64, 69, 16, 80, 13, 67, 58, 95, 88 };
    int b[] = { 42, 80, 61, 95, 43, 58, 36, 31, 87, 96,
        41, 64, 92, 69, 16, 13, 6, 67, 45, 88 };
#else
    int a[] = {63, 7, 56, 22, 11, 29, 2, 28, 32, 4,
        14, 0, 24, 68, 59, 70, 30, 18, 71, 83 };
    int b[] = { 14, 63, 7, 71, 30, 83, 56, 22,  29, 2, 
        59, 32, 4, 0, 24, 28, 68,  70,  11, 18,};
#endif

    int isTaller = 0;
    AVLTree t = NULL;
    for (int i = 0; i < NodeNum; ++i) {
        insertAVLTree(&t, a[i], &isTaller);
        //traversal(t);
        //printf("\n");
    }
    traversal(t);
    printf("\n");
    
    int isShorter = 0;
    for (int i = 0; i < NodeNum; ++i) {
        printf("delete %d:\n", b[i]);
        deleteAVLTree(&t, b[i], &isShorter);
        traversal(t);
        printf("\n");
    }

    return 0;
}

删除节点例子

int a[] = { 42, 61, 96, 43, 36, 31, 45, 87, 6, 41,
        92, 64, 69, 16, 80, 13, 67, 58, 95, 88 };
    int b[] = { 42, 80, 61, 95, 43, 58, 36, 31, 87, 96,
        41, 64, 92, 69, 16, 13, 6, 67, 45, 88 };

按a数组顺序插入节点，按b数组顺序删除节点。

a数组插入完是这样的：

1.删除42

递归找打它的前驱是41，41才是实际free掉的节点，42节点只需要将data改成41就行了。

由于41没了，递归弹栈过程修改上层节点bf，36的bf变为0，由于36为根节点的子树变矮了，继续更新31的bf，31的bf变为1，31为根节点的子树没有变矮，故不需要再更新42的bf。

 

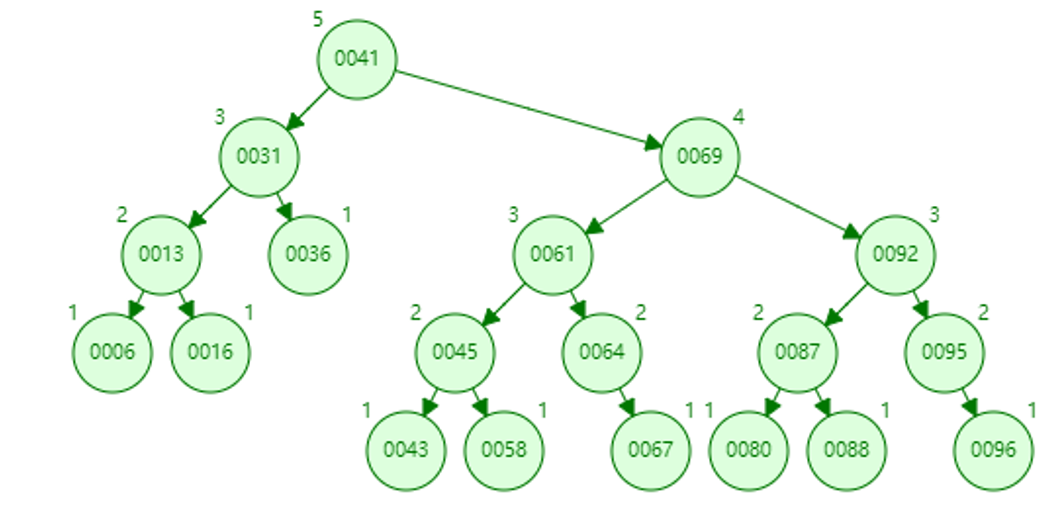
2.删除80

叶子节点，直接free，更新87的bf为-1，不需要再更新上层节点bf。 

 

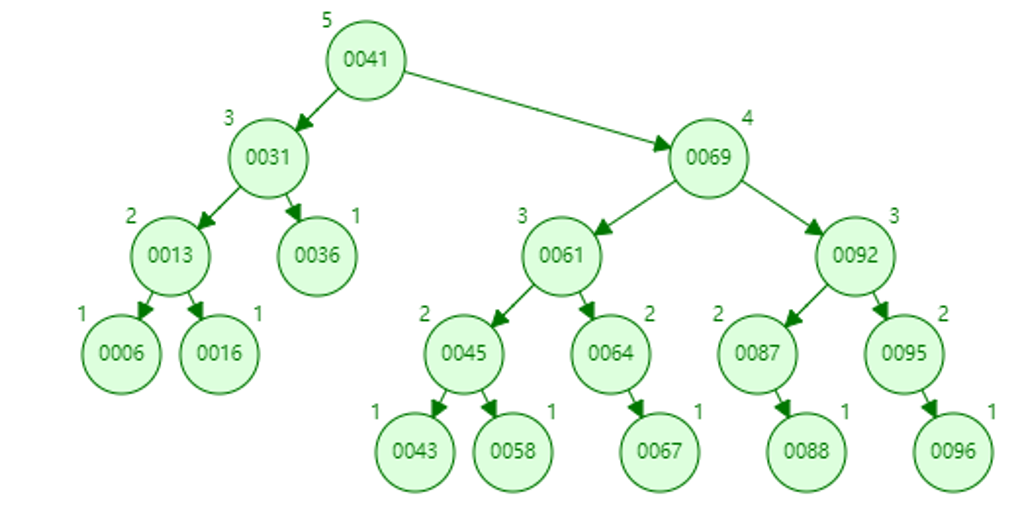
3.删除61

找到前驱58，更新45的bf为1，61的data改成58。

 

 

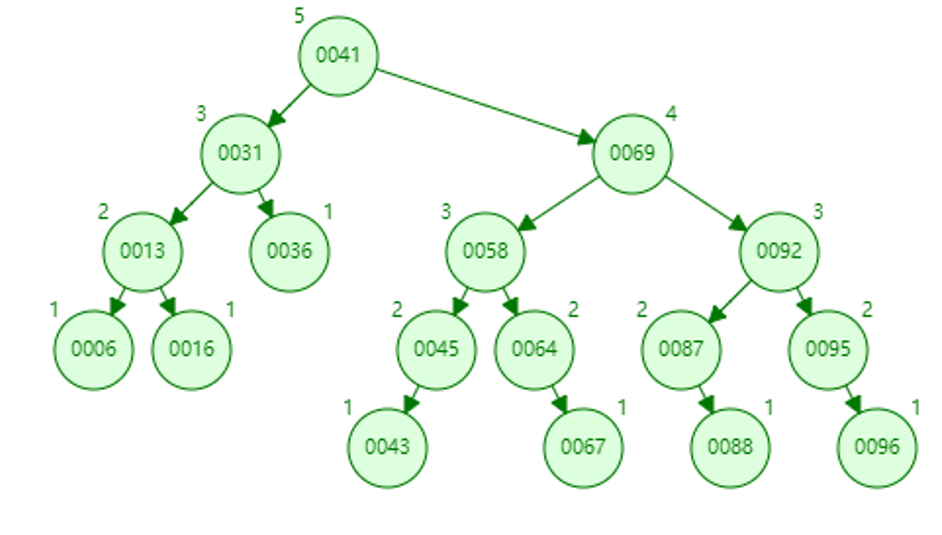
4.删除95

95的data更新为96，95的bf更新为0，free掉96，更新92的bf为1。

 

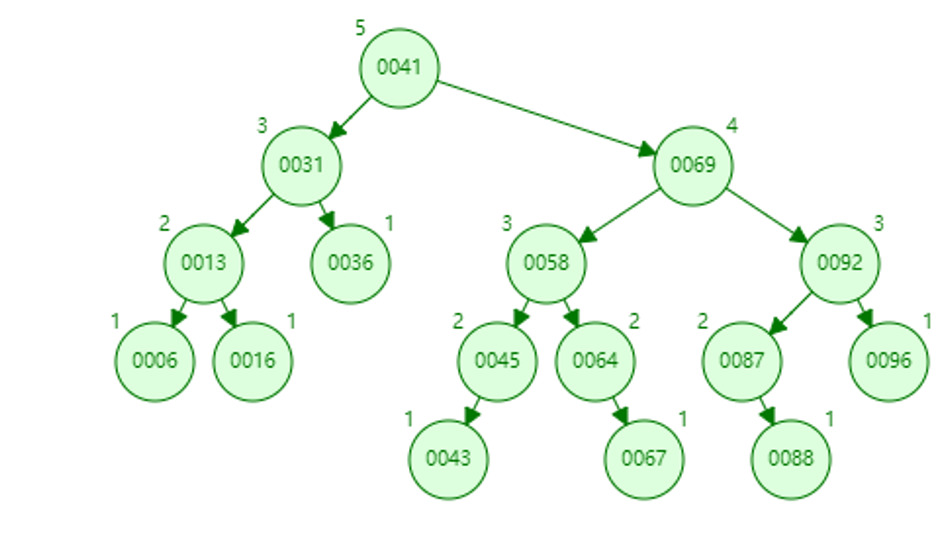
5.删除43

叶子节点，直接free，更新45的bf为0，58bf为-1。

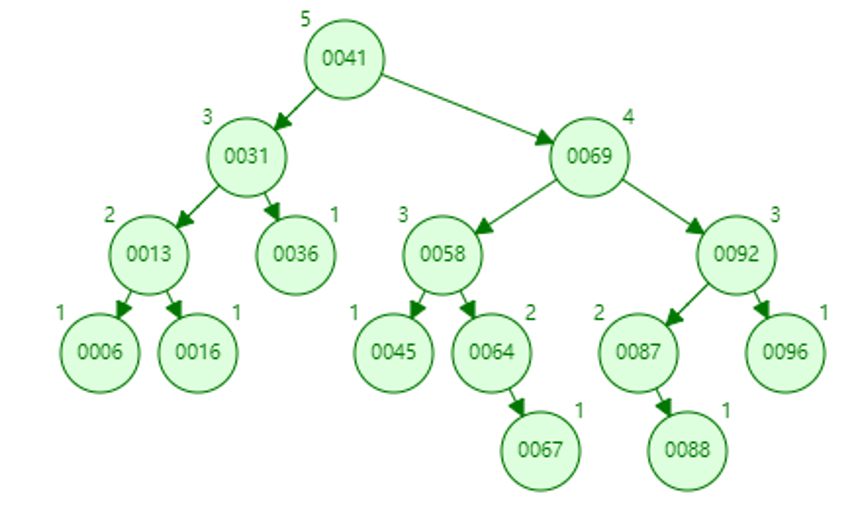
6.删除58

找到前驱45，58的data改成45，释放45。这时候58的bf是-2（代码里是不存在2和-2这个状态的），需要重新平衡，RR型，一个左旋完事。balanceRight已经调整45，64，67三个节点的bf了。平衡后58这颗子树变矮了，所以需要更新69的bf为-1。

 

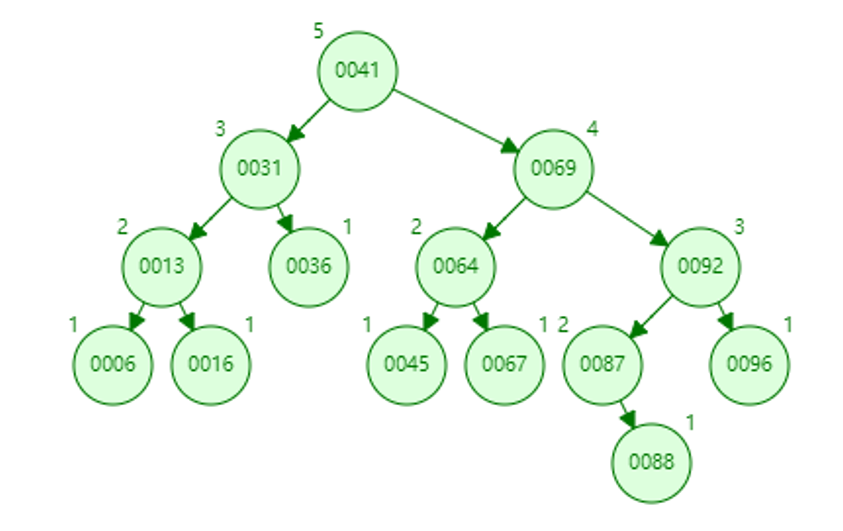
7.删除36

叶子节点，直接free。31的bf是2，需要重新平衡。注意31的左孩子13的bf是0，如果是插入导致的不平衡是不会出现这种情况的。这里直接看成LL型，右旋后13的bf更新为-1。由于t没有变高（平衡后是13），则不需要再更新上层节点bf，*isShorter变为0。

 

 

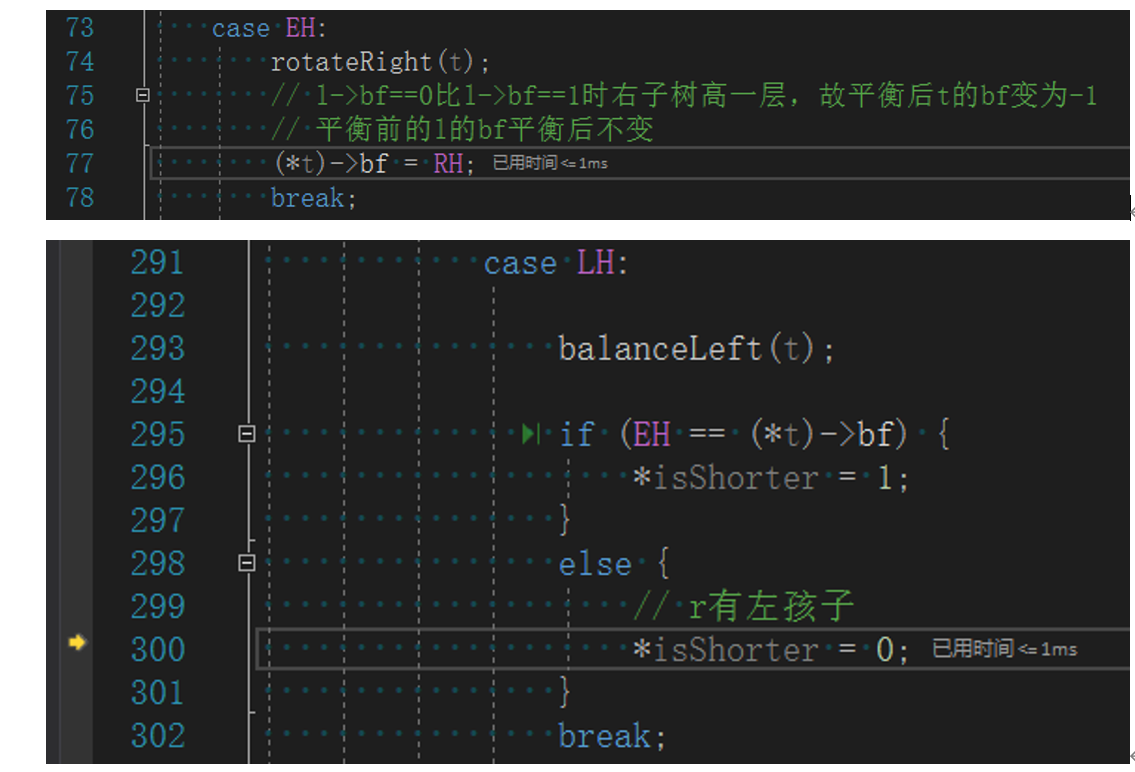
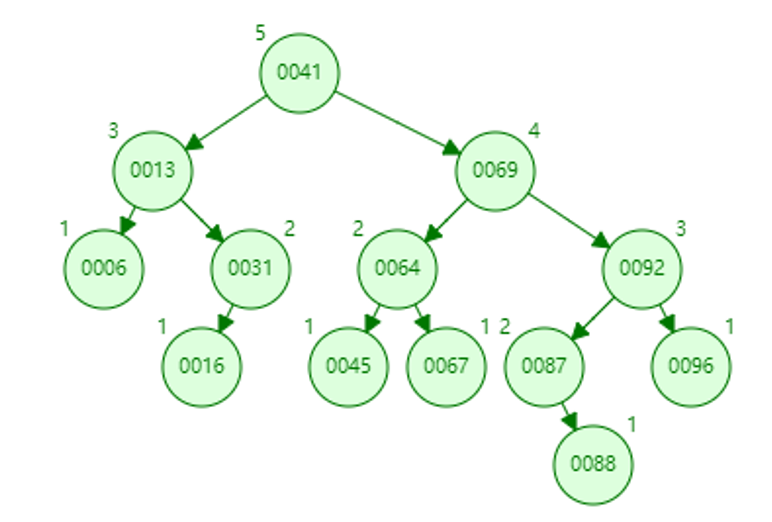
8.删除31

31的data更新为16，更新31的bf为0，free掉16。更新13的bf为0，变矮了继续检查41的bf，41的bf变为-2，故重新平衡。这时候右孩子69的bf是-1，看作RR型，直接左旋。

 

9. 删除87

87的data变为88，free掉88。88的bf变为0，更新92的bf为0。

 

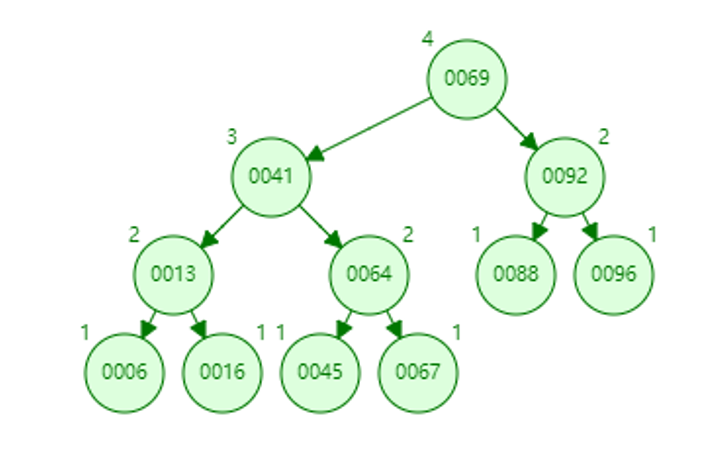
10.删除96

叶子节点，直接free掉，更新92的bf为1。

 

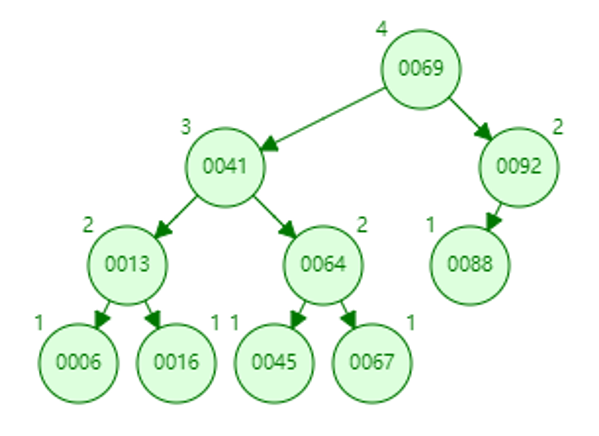
11. 删除41

找到前驱16，41的data更新为16。更新13的bf为1。树没有变矮。

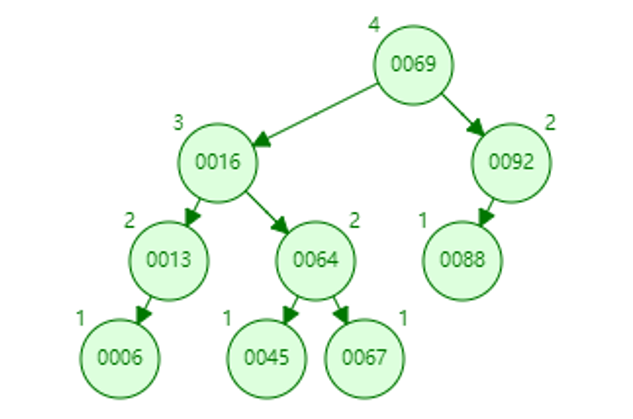
12. 删除64

找到前驱45，64的data更新为45。64的bf更新为-1。

 

13. 删除92

更新92的data为88，更新92的bf为0，free掉88。这时候69的bf为2，需要重新平衡。69的左孩子16的bf为0，直接右旋，更新16的bf为-1。

 

 

14．删除69

找到前驱67，69的data更新为67，free掉67，更新45的bf为0。更新67的bf为0。

 

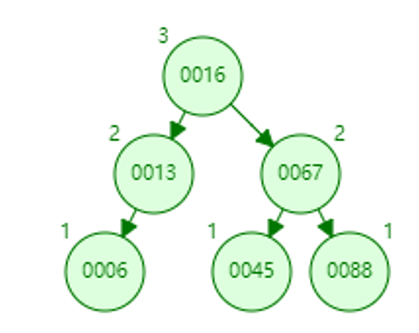
15. 删除16

找到前驱13，更新16的左孩子为6。

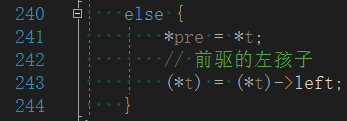
替换16的data为13，free掉13。

 

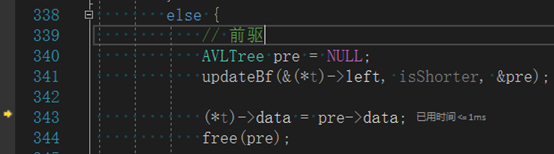
更新新的13的bf为-1。

 

16.删除13

找到前驱6，更新13的data为6。此时新的6的bf是-2，需要重新平衡。6的右孩子67的bf是0，直接看成RR型，左旋，并更新67的bf为1。平衡后高度不变。

 

 

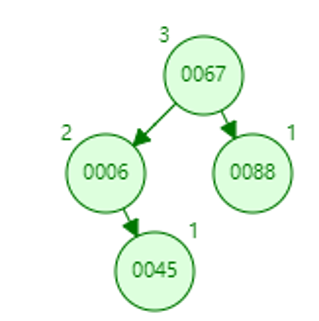
17.删除6

6的data更新为45，6的bf更新为0。变矮了，67的bf更新为0。

 

 

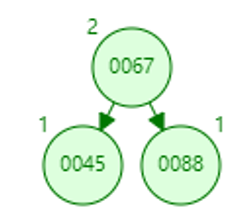
18. 删除67

找到前驱45，更新67的data为45，free掉45。更新67的bf为-1。

19. 删除45

更新45的data为88，bf为0，free掉88。

 

 

20.删除88

直接free掉。

 

 

利用高度实现平衡二叉树

待更新

他过江
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
LR(即L-1AL)转换求特征值(python,数值积分)
seventonight的博客
05-07 741
第三十三篇 经过LR转换求特征值 三对角矩阵特征值的LR变换 一种最适用于稀疏(带宽或三对角化)矩阵的转化方法叫做“LR”变换。这是类似于之前描述[L][U]因式分解。 对于迭代变换的任意步骤k。也可以把矩阵写成一个上三角与一个下三角乘积的形式，详情可见LU分解解方程 从上面的式子可以得到 再代入第二个式子 表明[L]具有变换矩阵[P]所要求的性质，详情可见特征值编程基础。所以随着迭代的进行，变换后的矩阵[A]k趋向于一个特征值等于对角项的上三角矩阵。 计算实例 对于一个非对称矩阵的‘LR’分解
平衡二叉树详解 通俗易懂
m0_61886762的博客
06-16 1万+
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点的时候，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡树。在保持二叉排序树特性的前提下，调整最小不平衡树中各结点之间的连接关系，进行相应的旋转，使之称为新的平衡子树。 为了我们以后的讲解看起来更加轻松一点，我们先讲述一个平衡二叉树构建过程的例子。假设我们现在有一个数组a【10】={ 3,2,1,4,5,6,7,10,9,8}需要构建二叉排序树。在没有学习平衡二叉树之前，根据二叉排序树的特性，我们通常会将它构建称为图5的样子。.
平衡二叉树详解
热门推荐
尽量致力于发表微服务、中间件和算法等原创作品。
06-17 4万+
平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。 平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入删除的时候平衡二叉树的平衡可
平衡二叉树（详细解释+完整C语言）
weixin_54186646的博客
05-03 1万+
平衡二叉树的插入与删除操作的详细解释与完整C语言代码
三步学会构建平衡二叉树（简单好理解）
湖水微澜
11-15 8623
平衡二叉树的构建
编译原理——理解LL/LR/SLR/LALR
Xixoqw的博客
04-21 7820
LL（1）文法 属于自上而下的分析方法。 也就是说，同一个非终结符的多种递推方式中，首字母一定不同。这样就可以只用根据一个首字母就可以判断出是哪一个递推式子。 文法名字由来 第一个L代表从左边开始扫描； 第二个L表示产生最左推导 数字1表示每一步推导式只需要向后看一个符号就可以 LL(1)文法的明显性质 没有公共左因子（如果有，那么无法只读一个字符就判断如何递归） 不是二义的（每个读入的字符都...
数据结构快速入门
05-02
4. **树结构**：树是一种非线性数据结构，包括二叉树（二分查找树、平衡二叉树如AVL树和红黑树）、堆（最大堆和最小堆）、树的遍历（前序、中序、后序）等。这些在搜索、排序和优先级队列中广泛应用。 5. **图结构*...
ACMer 入门级算法模板
02-19
- 树：包括二叉树、平衡树（AVL、红黑树）、堆（最大堆、最小堆）。 - 图：存储顶点和边的关系。 7. **递归与回溯**： - 递归：函数调用自身，用于解决分治问题。 - 回溯：在解决问题时尝试所有可能的路径，...
ACM入门课程资料PPT
07-16
接下来，PPT可能会深入讲解数据结构，如栈、队列、链表、树（二叉树、平衡树如AVL和红黑树）、图等，因为它们是构建复杂算法的基石。此外，动态规划、贪心策略和回溯法等高级算法也会有所涉及，这些都是ACM竞赛中...
数据结构和算法笔记与快速入门.zip
最新发布
06-17
这份"数据结构和算法笔记与快速入门.zip"压缩包文件显然包含了丰富的学习资源，旨在帮助大学生和初学者掌握这一领域的核心概念。 数据结构是组织、管理和存储数据的方式，它决定了数据的逻辑结构和物理结构。主要的...
逻辑回归（LR）的原理及其推导
june_young_fan的博客
11-07 2235
一、逻辑回归 1.1 分类问题 在分类问题中，你要预测的变量 yyy 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前使用最广泛的学习算法之一。 在分类问题中，我们尝试预测的是结果是否属于某一个分类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；区别一个肿瘤是恶性的还是良性的等等。 我们从二元的...
2017-910-十二
qq_43640181的博客
08-11 411
题目 二叉树结点的平衡因子（bf）定义为该结点的左子树高度与 右子树高度之差。设二叉树结点结构为：(lchild,data,bf,rchild), lchild,rchild 是左右儿子指针；data 是数据元素；bf 是平衡因子，编写递归算法计算二叉树中各个结点的平衡因子。 思路 通过后序遍历来遍历二叉树的每一个结点，然后计算每一个结点平衡因子。平衡因子等于左子树高度与右子树高度之差。故需要求出左子树和右子树的高度，也是算法的核心难点。 求出左子树和右子树的高度的算法是high（TreeNode * t）
数据结构之平衡二叉树（AVL）
ZHAO
06-14 263
一、概念    平衡二叉树是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。    平衡因子（BF）：结点的左子树深度减去右子树深度的值称为平衡因子。    最小不平衡子树：插入进来一个元素后，变得不平衡的最小部分。二、实现原理三、代码实现...
平衡二叉树
LF19971222的博客
02-21 836
概念： 结点的平衡因子：二叉树中某结点左子树的高度与右子树的高度之差称为该结点的平衡因子。 平衡二叉树是另一种形式的二叉查找树。 其特点是：左右子树深度之差的绝对值不大于1 称有这种特性的二叉树称为平衡二叉树。 在算法中，可以通过平衡因子来具体实现平衡二叉树的定义。 从平衡因子的角度可以说，若一颗二叉树中所有结点的平衡因子的绝对小于或等于1，则该数称为平衡二叉树。 1.LL型调整 2.RR型调整 3.LR型调整 4.RL型调整 平衡二叉树中结点的插入与建立 .
震惊！！！平衡二叉树居然还有这种学习方法！！
BackToMe的博客
08-08 7491
请要相信我，30分钟让你掌握AVL树（平衡二叉树） 作者：u011469062 请要相信我，30分钟让你掌握AVL树（平衡二叉树） 前言：本文不适合 给一组数据15分钟就能实现AVL的插入和删除操作的大牛（也请大牛不要打击小菜）本文适合，对avl还不了解，还没有亲自实现avl的插入和删除操作的同学ps，你在嘲笑楼主的题目时，你已证明了自己正在嘲笑自己的智商。我们要善于
数据结构之平衡二叉树的平衡因子BF 的计算
followMyInclinations的专栏
12-29 1万+
在书上看了平衡二叉树的代码后，发现前人的智慧真是无限。但是因为一次性给出的最完美的代码让人有时候看不太懂... 后来经过仔细推敲，才慢慢发现了其中的奥秘。一开始并不知道关于平衡二叉树的平衡因子BF是怎么修改的，后来才发现关于平衡二叉树的最重要的一句话：在构建平衡二叉树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树，在保持二叉排序树特性的前提下，调整关
查找——平衡二叉树Balanced Binary/Height-Balanced Tree的详解与实现
lseaJK的博客
06-29 1015
查找8.5 平衡二叉树8.5.1 平衡二叉树的定义8.5.2 平衡旋转8.5.3 插入结点8.5.4 删除结点其他 8.5 平衡二叉树 在二叉排序树上实现查找的时间复杂度与从根到所查数据元素的结点的路径长度成正比，在最坏情况下这个长度等于树的高度。在构造二叉排序树时，如果输入的数据元素序列恰巧按其关键字大小有序，则在形式上已经退化成一个单链表了。这样查找操作所需要的时间就是O(n),或者说与结点个数成线性关系。 因此需要有一种方法来避免使二叉排序树变得过于窄而高这种情况的发生。如果能够保证树的高度与树中结点
掌握二叉树与分治法：算法内功修炼入门
这有助于构建有序的数据结构，如二叉搜索树或平衡二叉树。 3. **分治法**： 描述中提到的分治法是一种常见的算法设计策略，通过将复杂问题分解为规模较小、相互独立的子问题来解决。例如，二分搜索就是基于分治...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值