B站up主——“DR-CAN”《动态系统建模》系列课程之电路系统建模_基尔霍夫定律的解题过程

这是UP主的课程视频，讲的非常nice！强烈推荐大家去听听！https://www.bilibili.com/video/BV13t411t7aR/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=47f1775a430f1dd9bcb3807911fae015

一、题目电路图及参数

       课程中UP主提供的电路图及相关元器件的参数如下图所示：

 

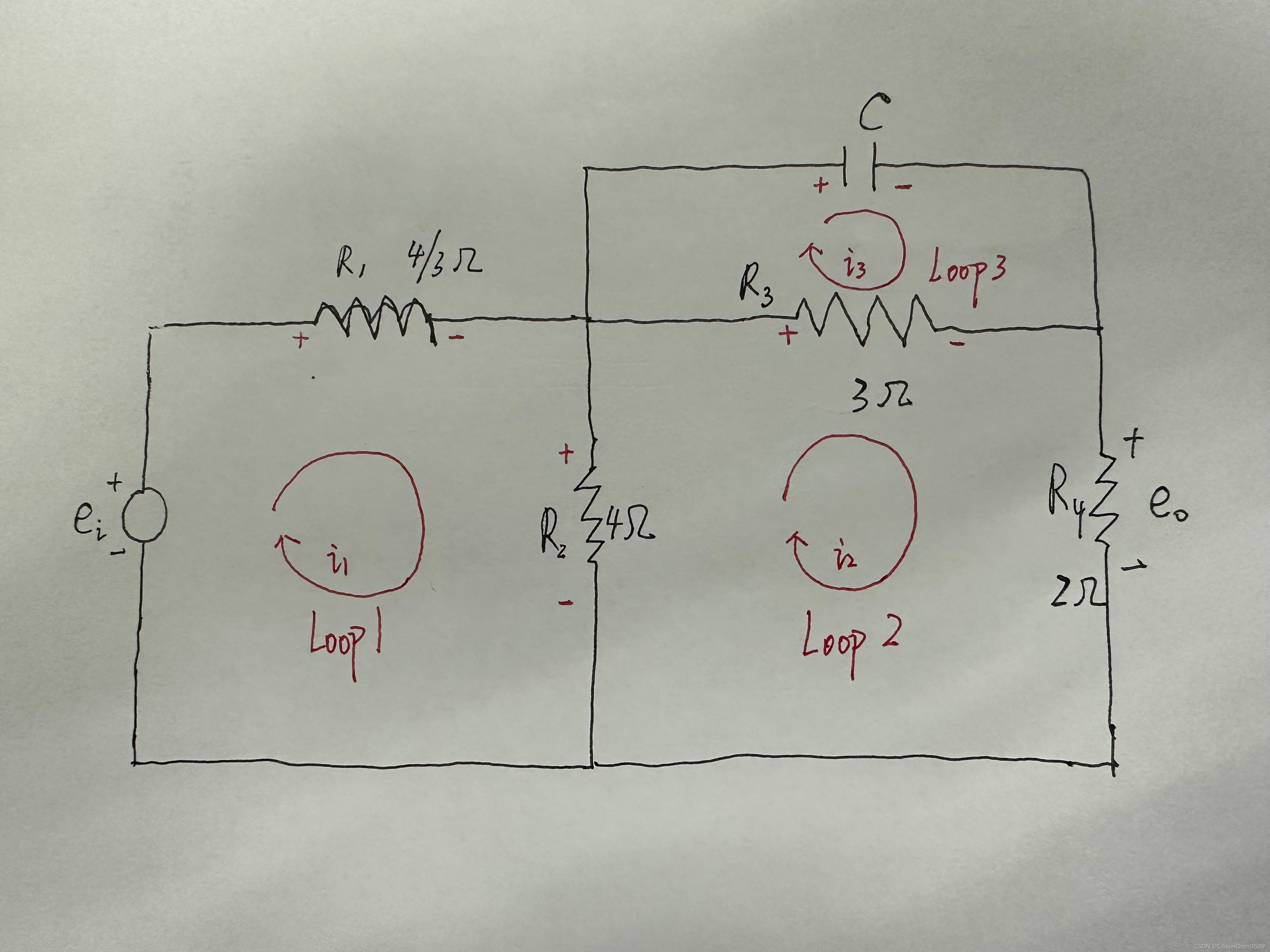
注：

       

           

       
       

二、各个回路的KVL方程

Loop1：

              根据“注”所示，带入Loop1的方程可得：

              

              根据上式，可得

Loop2：

              根据“注”所示，带入Loop2的方程可得：

              

              根据Loop1所得，可得：

Loop3：

              根据“注”所示，带入Loop3的方程可得：

             

              根据Loop1、Loop2所得，即可得到关于、的微分方程：