FFT算法的实现（2）

最新推荐文章于 2024-09-06 16:54:11 发布
最新推荐文章于 2024-09-06 16:54:11 发布
阅读量5.1k 收藏 68
点赞数 4
分类专栏： 单片机 文章标签： fft arduino 快速傅里叶变换 C语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Egean/article/details/53258286
版权

上一篇文章当中已经推导出了整个频域上的表达式，这个表达式叫做蝶形运算，下面就借由蝶形运算实现FFT算法。

那么首先就要先说说蝶形运算。蝶形运算听着挺高大上的，但可以有一种简单方便的图形表示方法，为方便起见我这里再贴一次公式：

X [ k ] = X 0 [ k ] + W N k X 1 [ k ] X[k]=X_0[k]+W_N^{k}X_1[k] X[k]=X0​[k]+WNk​X1​[k]
X [ k + N 2 ] = X 0 [ k ] − W N k X 1 [ k ] X[k+\frac N2]=X_0[k]-W_N^{k}X_1[k] X[k+2N​]=X0​[k]−WNk​X1​[k]

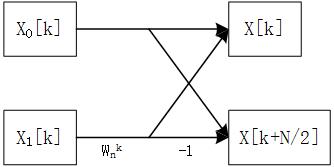
那么这个蝶形运算可以用图形表示为

fig1

当然，可以看出一次蝶形运算虽然简化了运算，但仍然需要知道 X 0 [ k ] X_0[k] X0​[k] 和 X 1 [ k ] X_1[k] X1​[k] ，就是说在进行蝶形运算之前我们仍需对 x 0 [ n ] x_0[n] x0​[n] 和 x 1 [ n ] x_1[n] x1​[n] 进行DFT得到 X 0 [ k ] X_0[k] X0​[k] 和 X 1 [ k ] X_1[k] X1​[k] 然后才能得到完整的 X [ k ] X[k] X[k] ，我们知道DFT运算起来是很麻烦的，但是注意到，这里DFT的运算量已经减少了一半，也就是每次只对 N 2 \large \frac N2 2N​个点进行DFT，那么可以由此得到启示，能不能像得到 X [ k ] X[k] X[k] 一样通过蝶形运算来得到 X 0 [ k ] X_0[k] X0​[k] 和 X 1 [ k ] X_1[k] X1​[k] 呢？这是可以的，对于 X 0 [ k ] X_0[k] X0​[k] 只需将其分为奇偶两组，然后再通过一次蝶形运算即可得到 X 0 [ k ] X_0[k] X0​[k] ，这时单次DFT的运算量为 N 4 \large \frac N4 4N​，重复以上过程，直到DFT的运算量为1，此时就会出现一个有趣的事情：

X [ 0 ] = ∑ n = 0 0 x [ n ] e − i 2 π ∗ 0 N n = x [ 0 ] X[0]=\sum\limits_{n=0}^{0} x[n]e^{-i\frac{2\pi *0}{N}n}=x[0] X[0]=n=0∑0​x[n]e−iN2π∗0​n=x[0]

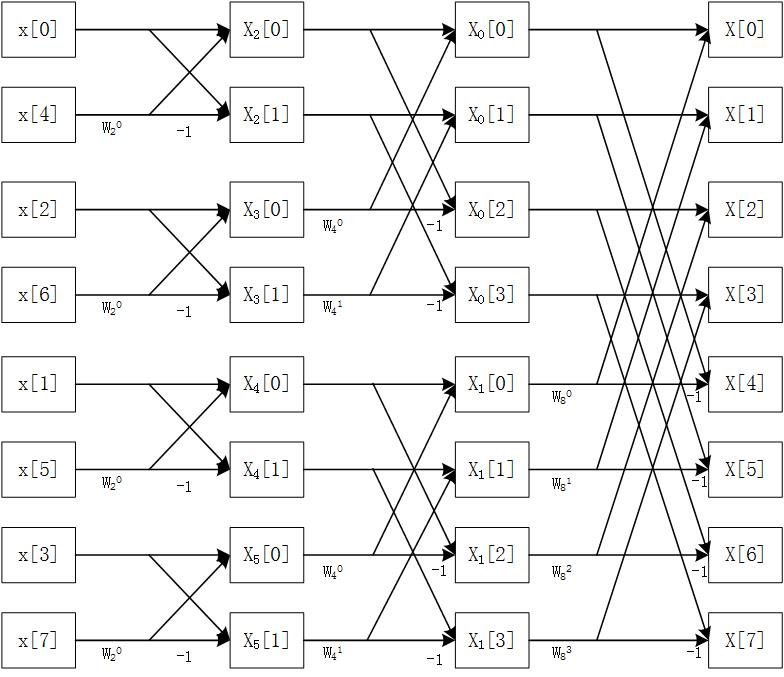
此时就不需进行DFT了，直接进行蝶形运算就可以了，这就是FFT算法。以上的说明可能比较抽象，下面举一个8点FFT的例子，假设使用 x [ 0 ] x[0] x[0]$x[7]$表示要进行FFT的8个点，用$X[0]$ X [ 7 ] X[7] X[7]表示对应频域上的点，那么根据以上思路，需先将0~7分为奇偶两组，即：{0,2,4,6}和{1,3,5,7}，然后继续分组：{0,4}和{2,6}、{1,5}和{3,7}，最后一次分组：{0}和{4}、{2}和{6}、{1}和{5}、{3}和{7}。经过三次分组后发现DFT的运算量已经是1了，这时再进行蝶形运算，如下图：

这里写图片描述

按照这个图我们只需要用程序实现这个图，就可以得到FFT的结果。但是在此之前还有一件事，就是分组问题，可以看到我们首先需要将01234567的顺序换为04261537的顺序，这个顺序有什么规律呢？将其转换为二进制可以看到：000、100、010、110、001、101、011、111。其实就是逆向的二进制加法，最左边为最低位，最右边为最高位，从低位开始加1，然后向高位进位。
所以要完成一个FFT分两步，第一步先将拿到的数组进行逆序，第二步进行蝶形运算。第二步的是最复杂的，但总的可以将其看成两个for循环来实现，以上图为例，8点的FFT需要进行3次蝶形运算，每一次蝶形运算又分为几个单次的蝶形运算，如第1次蝶形运算就分为4个小的单次蝶形运算。

先给出C语言版本（话说啥时候用结构体重构一下。。。）

/* linux下gcc编译 */
#define _USE_MATH_DEFINES
#include <math.h>
#include <stdio.h>
#include <stdint.h>
#include <sys/time.h>
#include <time.h>

#define FFTN 32  //fft的点数
#define PWE 5    //2^PWE=NFFT
#define LEN FFTN*2
#define FRE 2000      //采样频率
#define RS 62.5       //分辨率=FRE/FFTN
//由于一个点是复数，因此用偶数脚标表示实部，奇数脚标表示虚部

float fft_input[LEN] = {0,0,1,0,2,0,3,0,4,0,5,0,6,0,7,0,
                         8,0,9,0,10,0,11,0,12,0,13,0,14,0,15,0,
                         16,0,17,0,18,0,19,0,20,0,21,0,22,0,23,0,
                         24,0,25,0,26,0,27,0,28,0,29,0,30,0,31,0};
                         
                         /*
float fft_input[LEN] = {31,0,30,0,29,0,28,0,27,0,26,0,25,0,24,0,
                         23,0,22,0,21,0,20,0,19,0,18,0,17,0,16,0,
                         15,0,14,0,13,0,12,0,11,0,10,0,9,0,8,0,
                         7,0,6,0,5,0,4,0,3,0,2,0,1,0,0,0};
                         */
float fft_output[LEN];
float MAX[2]; //保存最后得出的结果

int ReverseArrange(void);
int Redix2FFT(void);
void IntegrateData(void);

void main(void)
{
  int i;
  clock_t begin, end;
    
  begin = clock();
  ReverseArrange(); //倒序
  Redix2FFT();  //FFT变换
  end = clock();
  printf("%lfs\n",(double)(end-begin)/CLOCKS_PER_SEC);

}
/*倒序函数，将fft_input进行逆向排序
 *               0   1   2   3   4    5     6     7
   倒序前脚标： 0-1 2-3 4-5 6-7 8-9 10-11 12-13 14-15
                 0   4   2    6    1    5    3    7
   倒序后脚标： 0-1 8-9 4-5 12-13 2-3 10-11 6-7 14-15
*/
//其中：2^PWE=NFFT，PWE表示次幂，即脚标由几位二进制组成
int ReverseArrange(void)
{
  int8_t i,j;
  int8_t tmp = 0x00;  //用来表示脚标
  //先给第一个复数赋值
  fft_output[0] = fft_input[0];
  fft_output[1] = fft_input[1];
  //对剩下的数进行倒序
  for(i=0;i<(FFTN-1)*2;i+=2){
      j = PWE-1;  //得出需要左移的位数
      //逆向二进制加法
      while((tmp & (1<<j)) != 0){
          tmp &= ~(1<<j); //把第j位置零
          j--;
      }
      tmp |= (1<<j);  //这里最后得出的是：0 4 2 6 1 5 3 7
      fft_output[i+2] = fft_input[tmp*2];   //按照新的顺序给输出赋值
      fft_output[i+3] = fft_input[tmp*2+1];
  }
  return 1;
}

/*基2fft运算，需先将fft_input倒序输入到fft_out中*/
int Redix2FFT(void)
{
  int8_t layer; //表示FFT的层数
  int8_t pmul; //= 2^(PWE - layer)，表示当前层中需要进行几次小FFT，FFTN/pmul表示当前小FFT的点数
  int8_t i; //表示正在进行第几次小FFT
  int8_t j; //= 2^(layer - 1)，表示当前层小FFT中蝶形运算的次数
  int8_t k; //每次小FFT中，正在进行第几次蝶形运算
  int8_t currentBase; //表示当前层的小FFT中，第一个元素的脚标
  int8_t current; //=currentBase + k，表示当前需要进行蝶形运算的元素的脚标
  int8_t another; //=current + j，表示当前需要进行蝶形运算的元素的脚标
  int8_t m;
  float Re,Im; //实部、虚部的暂存区
  float TPOA;  //=2 * pi / FFTN，FFT旋转因子WNK的w值
  float TPOATP;//=TPOA * pmul，表示小FFT中WNK的w值
  float reFactor,imFactor;  //=cos(TPOATP * k)，=-sin(TPOATP * k)，表示WNK的实部和虚部

  //下面的注释假设FFTN=8

  TPOA = 2 * M_PI / FFTN; //TPOA = PI/4
  for(layer=1;layer<=PWE;layer++){  //layer = 1,2,3
    j = 0x01<<(layer-1);  //使用math中的pow()会出现bug，使用左移运算减轻计算量
    pmul = 0x01<<(PWE - layer);
    for(i=0;i<pmul;i++){  //pmul=4时，i = 0,1,2,3
      currentBase = i * 4 *j;   //j = 1时，currentBase = 0,4,8,12
      TPOATP = TPOA * pmul;   //pmul=4时，TPOATP = PI
      for(k=0;k<j;k++){   //j=1时，k=0
         current = currentBase + k*2; //current = 0,4,8,12;
         another = current + j*2; //another = 2,6,10,14;
         //准备WNK
         reFactor = cos(TPOATP * k); //1
         imFactor = -sin(TPOATP * k);//0
         //乘上WNK
         Re = fft_output[another];  //备份实部
         fft_output[another] = fft_output[another] * reFactor 
            - fft_output[another+1] * imFactor; //fft_output[2] = 8
         fft_output[another+1] = fft_output[another+1] * reFactor
            + Re * imFactor;  //fft_output[3] = 0
         //蝶形加法
         Re = fft_output[current];  //Re=0
         Im = fft_output[current+1];  //Im=0
         fft_output[current] += fft_output[another];  //fft_output[0] = 8;
         fft_output[current+1] += fft_output[another+1];  //fft_output[1] = 0

         fft_output[another] = Re - fft_output[another];  //fft[2] = -8
         fft_output[another+1] = Im - fft_output[another+1];  //fft[3] = 0
      }
    }
  }
  for(m = 0; m < LEN; m += 2) {
     printf("[%d]: %f+%fi\n", m/2, fft_output[m], fft_output[m+1]);
  }
}
 /* 输出整合，计算出每个频率的幅值，取出幅值最大的点
  */
void IntegrateData(void)
{
  //计算复数的模，注意，所有的模都存到偶数项中
  //fft_output[0] = sqrt(fft_output[0]*fft_output[0]+fft_output[1]*fft_output[1])/FFTN;
  fft_output[LEN-2] = sqrt(fft_output[LEN-2]*fft_output[LEN-2]+fft_output[LEN-1]*fft_output[LEN-1])/FFTN;
  for(uint8_t i=2;i<(LEN-2);i+=2){ //最后一个点和第一个点已单独处理
    fft_output[i] = 2*sqrt(fft_output[i]*fft_output[i]+fft_output[i+1]*fft_output[i+1])/FFTN;
  }
  //找出其中模长最大的值，记录脚标和模长
  MAX[0] = 2;   //脚标
  MAX[1] = fft_output[2]; //模长
  for(uint8_t i=4;i<LEN;i+=2){
    if(MAX[1]<fft_output[i]){   //替换
      MAX[0] = i;
      MAX[1] = fft_output[i];
    }  
  }    
}

下面将这个算法在Arduino上实现，注释已经写得很完善了，这里就不多加说明。

/*从ADC读取数值后，使用FFT对波形进行分析，得出其中所含频率和对应幅度*/
/*  FFTN    fft时间（ms）  求最值时间(ms) 
 *   8         4  
 *   16        10 
 *   32        25              2
*/
#include <math.h>
#define FFTN 32  //fft的点数
#define PWE 5    //2^PWE=NFFT
#define LEN FFTN*2
#define FRE 2000      //采样频率
#define RS 62.5       //分辨率=FRE/FFTN
//由于一个点是复数，因此用偶数脚标表示实部，奇数脚标表示虚部
float fft_input[LEN] = {0,0,1,0,2,0,3,0,4,0,5,0,6,0,7,0,
                         8,0,9,0,10,0,11,0,12,0,13,0,14,0,15,0,
                         16,0,17,0,18,0,19,0,20,0,21,0,22,0,23,0,
                         24,0,25,0,26,0,27,0,28,0,29,0,30,0,31,0};
                         
float fft_output[LEN];
float MAX[2]; //保存最后得出的结果
unsigned long curTime,lastTime;
void setup() {
  Serial.begin(115200);
}

void loop() {
  ReverseArrange(); //倒序
  lastTime = millis();
  Redix2FFT();  //FFT变换
  curTime = millis();
  Serial.print("fft=");
  Serial.println(curTime-lastTime);
  /* 以上是fft */
  //lastTime = millis();
  //IntegrateData();
  //curTime = millis();
  //Serial.print("int=");
  //Serial.println(curTime-lastTime);
}
/*倒序函数，将fft_input进行逆向排序
 *               0   1   2   3   4    5     6     7
   倒序前脚标： 0-1 2-3 4-5 6-7 8-9 10-11 12-13 14-15
                 0   4   2    6    1    5    3    7
   倒序后脚标： 0-1 8-9 4-5 12-13 2-3 10-11 6-7 14-15
*/
//其中：2^PWE=NFFT，PWE表示次幂，即脚标由几位二进制组成
int ReverseArrange(){
  int8_t i,j;
  int8_t tmp = 0x00;  //用来表示脚标
  //先给第一个复数赋值
  fft_output[0] = fft_input[0];
  fft_output[1] = fft_input[1];
  //对剩下的数进行倒序
  for(i=0;i<(FFTN-1)*2;i+=2){
      j = PWE-1;  //得出需要左移的位数
      //逆向二进制加法
      while((tmp & (1<<j)) != 0){
          tmp &= ~(1<<j); //把第j位置零
          j--;
      }
      tmp |= (1<<j);  //这里最后得出的是：0 4 2 6 1 5 3 7
      fft_output[i+2] = fft_input[tmp*2];   //按照新的顺序给输出赋值
      fft_output[i+3] = fft_input[tmp*2+1];
  }
  return 1;
}

/*基2fft运算，需先将fft_input倒序输入到fft_out中*/
int Redix2FFT(){
  int8_t layer; //表示FFT的层数
  int8_t pmul; //= 2^(PWE - layer)，表示当前层中需要进行几次小FFT，FFTN/pmul表示当前小FFT的点数
  int8_t i; //表示正在进行第几次小FFT
  int8_t j; //= 2^(layer - 1)，表示当前层小FFT中蝶形运算的次数
  int8_t k; //每次小FFT中，正在进行第几次蝶形运算
  int8_t currentBase; //表示当前层的小FFT中，第一个元素的脚标
  int8_t current; //=currentBase + k，表示当前需要进行蝶形运算的元素的脚标
  int8_t another; //=current + j，表示当前需要进行蝶形运算的元素的脚标
  float Re,Im; //实部、虚部的暂存区
  float TPOA;  //=2 * pi / FFTN，FFT旋转因子WNK的w值
  float TPOATP;//=TPOA * pmul，表示小FFT中WNK的w值
  float reFactor,imFactor;  //=cos(TPOATP * k)，=-sin(TPOATP * k)，表示WNK的实部和虚部
  
  //下面的注释假设FFTN=8
  
  TPOA = 2 * PI / FFTN; //TPOA = PI/4
  for(layer=1;layer<=PWE;layer++){  //layer = 1,2,3
    j = 0x01<<(layer-1);  //使用math中的pow()会出现bug，使用左移运算减轻计算量
    pmul = 0x01<<(PWE - layer);
    for(i=0;i<pmul;i++){  //pmul=4时，i = 0,1,2,3
      currentBase = i * 4 *j;   //j = 1时，currentBase = 0,4,8,12
      TPOATP = TPOA * pmul;   //pmul=4时，TPOATP = PI
      for(k=0;k<j;k++){   //j=1时，k=0
         current = currentBase + k*2; //current = 0,4,8,12;
         another = current + j*2; //another = 2,6,10,14;
         //准备WNK
         reFactor = cos(TPOATP * k); //1
         imFactor = -sin(TPOATP * k);//0
         //乘上WNK
         Re = fft_output[another];  //备份实部
         fft_output[another] = fft_output[another] * reFactor 
            - fft_output[another+1] * imFactor; //fft_output[2] = 8
         fft_output[another+1] = fft_output[another+1] * reFactor
            + Re * imFactor;  //fft_output[3] = 0
         //蝶形加法
         Re = fft_output[current];  //Re=0
         Im = fft_output[current+1];  //Im=0
         fft_output[current] += fft_output[another];  //fft_output[0] = 8;
         fft_output[current+1] += fft_output[another+1];  //fft_output[1] = 0

         fft_output[another] = Re - fft_output[another];  //fft[2] = -8
         fft_output[another+1] = Im - fft_output[another+1];  //fft[3] = 0
      }
    }
  }
  for(int8_t m=0;m<FFTN*2;m++){
    Serial.print(fft_output[m]);  
    Serial.print("\t"); 
  }
  Serial.println("");
}
 /*输出整合，计算出每个频率的幅值，取出幅值最大的点
 */
void IntegrateData(){
  //计算复数的模，注意，所有的模都存到偶数项中
  //fft_output[0] = sqrt(fft_output[0]*fft_output[0]+fft_output[1]*fft_output[1])/FFTN;
  fft_output[LEN-2] = sqrt(fft_output[LEN-2]*fft_output[LEN-2]+fft_output[LEN-1]*fft_output[LEN-1])/FFTN;
  for(uint8_t i=2;i<(LEN-2);i+=2){ //最后一个点和第一个点已单独处理
    fft_output[i] = 2*sqrt(fft_output[i]*fft_output[i]+fft_output[i+1]*fft_output[i+1])/FFTN;
  }
  //找出其中模长最大的值，记录脚标和模长
  MAX[0] = 2;   //脚标
  MAX[1] = fft_output[2]; //模长
  for(uint8_t i=4;i<LEN;i+=2){
    if(MAX[1]<fft_output[i]){   //替换
      MAX[0] = i;
      MAX[1] = fft_output[i];
    }  
  }    
}
C++实现fft2函数功能（附完整源码）
希望我的博客，能帮上你解决学习中工作中所遇到的问题
06-26 298
C++实现fft2函数功能（附完整源码）
Matlab实现二维傅里叶变换（FFT2）
08-28
本程序主要实现了二维傅里叶变换，其中先对图像矩阵进行预处理（即图像中心化），然后进行行傅里叶变换，再对其进行列变换，进行行列变换是调用自己写的一维傅里叶变换函数ImFFT实现的。程序输入为图像矩阵A，输出为其傅里叶变换结果Fuv，并绘制了其频谱图
FFT算法
ResumeProject的博客
08-28 281
如果证充分条件两项都用拉格朗日
快速傅里叶变换（FFT）及其在多项式乘法中的应用 —— 深入分析与 Python 实现
最新发布
qq_52010229的博客
09-06 1625
单位根是指在复平面上均匀分布在单位圆上的点，满足 x^n = 1 的复数点。它们可以表示为：这些点的对称性和周期性使得我们可以通过分治法高效计算傅里叶变换。通过本文，我们深入探讨了如何利用快速傅里叶变换FFT进行高效的多项式乘法。我们从最基本的多项式操作出发，介绍了如何通过单位根和分治法将乘法复杂度从 O(n^2) 降低到 O(n log n)。我们还通过 Python 代码展示了 FFT 和 IFFT 的具体实现，并进行了多项式乘法的示例。FFT 在多项式乘法中的应用只是其众多用途之一。
Opencv实现MATLAB fft2 函数
rupture352的博客
04-06 949
毕设是图像处理方面的，在根据文献实现二维傅里叶变换时，因c++输出结果一直与MATLAB输出的不同，所以屡屡碰壁。 结果今天突然搞对了，很开心。 其实网上有实现代码，但因为没有明显以输出例子对比的，所以其实很多时候我已经实现对了，但因为输出形式不对，或者把复数形式计算成幅值输出，一直在修改，特地写这篇总结前人的成果，防止新人因输出形式不对一直在瞎调。参考博客：https://blog.csdn.net/keith_bb/article/details/53389819 先以一个一维数组为例： >&gt
[笔记]FFT算法
YinJianxiang的博客
05-15 2万+
前言 对于学通信的人来说，在学到数字信号处理时都会学到一个东东，叫做快速傅里叶变换(Fast Fourier Transform,简称FFT)。这东西真的挺有用的，但是只要有那么一点用的东西，就是特别难的。(现在也有很多不完整的地方，以后再补充~) 什么是FFT FFT，即为快速傅氏变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改...
FFT算法【初识】（一）
Aquamarine__的博客
08-02 1519
（一）离散傅里叶变换（DFT） DFT是傅里叶变换在时域和频域上都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应该将其看作经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换以高效计算DFT。 基本性...
FFT说明.zip_FFT算法的C语言实现_fft_fft 谐波_谐波算法_谐波计算
07-15
本资料包提供的是FFT算法的C语言实现，特别适用于理解和实践谐波计算。** **一、FFT算法概述** FFT是离散傅里叶变换（DFT）的一种高效算法，由Cooley和Tukey于1965年提出。它通过将大问题分解为小问题来减少计算量...
基于matlab的定点FFT算法实现
01-11
总的来说，基于MATLAB的定点FFT算法实现涉及数据类型的转换、自定义运算处理以及误差控制等多个环节，它为信号处理和硬件设计提供了灵活且高效的工具。通过深入理解和实践，我们可以更好地理解和利用这一技术，提升...
编程实现按时间抽取的基2FFT算法1
08-08
源代码可能分为DFT算法的实现和两种不同方法的FFT算法实现；测试用例可能包括不同的输入序列，用于验证算法的正确性；结果输出将展示计算的DFT和FFT结果，以及与MATLAB计算结果的对比；文档说明则会详述项目的实施...
DSP实验2 FFT算法实现 实验说明1
08-03
这意味着除了实现正确的FFT算法之外，你们还需要对算法有深入的理解，能够解释其工作原理，并且能够清晰地记录和展示实验过程和结果。这是一次全面考察你们在数字信号处理和MATLAB编程方面能力的机会。
FFT算法在单片机中的应用
04-27
快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。
51单片机fft算法
12-27
51单片机fft算法
FFT算法的C语言实现（可以直接用在单片机中）
06-03
FFT算法的C语言实现（在单片机上验证通过）
FFT算法的软件实现和应用
06-10
FFT算法的软件实现和应用.pdf
JAVA实现FFT算法
01-03
java实现FFT算法，关于快速傅里叶变换（FFT）和傅里叶变换的理论知识这里我就不提了，本文主要讲解FFT实现： 之前想找一个FFT代码，在网上找了很多都是有问题的，下面我完善了一个供大家学习交流；
FFT算法在单片机中的使用&&L…
effort0806222的博客
01-17 6027
原文地址：FFT算法在单片机中的使用&&LCD12864驱动作者：元大帝  好久没更新博客了，觉得对不起自己建立博客的初衷。我这个人太懒了，又没有坚持下去的决心，唉~     言归正传，本次创新基金我是要做一个简易的频谱仪，核心就是要进行一个FFT运算。大家知道，如果采用DSP芯片效果那是相当好的。但由于项目资金以及时间不够等情况，我采用的是ATMEL公司的AVR单片机，这款单片机的FLASH存储
FFT算法讲解——麻麻我终于会FFT了！
热门推荐
谁能代表肯德基
03-12 15万+
FFT——快速傅里叶变换 这块不写东西空荡荡的，我决定还是把FFT的定义给贴上吧 FFT（Fast Fourier Transformation）是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。 这三段话其实一点用也没有 FFT是干什么的 FFT在算法竞赛中就有一个用途：加速多项式乘法 ...
2fft算法实现
05-29
2fft算法是一种快速傅里叶变换（FFT）算法，可以在O(nlogn)的时间复杂度内对长度为2的幂次方的序列进行离散傅里叶变换（DFT）。 以下是2fft算法的实现步骤： 1. 将长度为n（为2的幂次方）的序列分为两个长度为n/2的序列，分别为偶数项和奇数项。 2. 对这两个子序列分别递归应用2fft算法，得到它们的DFT。这里可以使用位逆序重新排列子序列，以便后面的合并操作。 3. 合并这两个DFT，得到原序列的DFT。合并时，可以利用旋转因子进行计算，具体方法为将偶数项的DFT加上旋转因子乘以奇数项的DFT。 4. 对合并后的DFT进行位逆序排列，得到原序列的DFT。 下面是2fft算法的Python实现代码： ```python import cmath def fft2(x): n = len(x) if n == 1: return x even = fft2(x[0::2]) odd = fft2(x[1::2]) factor = cmath.exp(-2j * cmath.pi / n) w = 1 for i in range(n // 2): x[i] = even[i] + w * odd[i] x[i + n // 2] = even[i] - w * odd[i] w *= factor return x ``` 这里使用了Python的cmath库，其中exp函数用于计算复数的指数函数，pi为圆周率。函数fft2接收一个长度为2的幂次方的序列x，返回它的DFT。
评论 11
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值