斜率优化dp

算法介绍

使用条件

形如 d p [ i ] = m i n { A ( i ) × B ( j ) + C ( i ) + D ( j ) } dp[i]=min\{A(i)\times B(j)+C(i)+D(j)\} dp[i]=min{A(i)×B(j)+C(i)+D(j)}的转移方程可尝试使用斜率优化。
（取$max$是类似的，本文不赘述）

法一：线性规划

考虑把 $dp[i]=A(i)\times B(j)+C(i)+D(j)$ 化成$y=kx+b$的形式，其中$y,x$只与$j$有关，$k,b$只与$i$有关，且 $x$严格单调递增。

则有：
$D(j)=-A(i)\times B(j)+dp[i]-C(i)$
其中$y=D(j),k=-A(i),x=B(j),b=dp[i]-C(i)$

在平面直角坐标系上把所有的$(x_j,y_j)$（即$(B(j),D(j))$）标出来。
要令$dp[i]$最小，则要令$b$最小，即是要找到某一点$(x_j,y_j)$，使斜率为$k$的直线经过该点时算出来的$b$最小。
发现只有 在给出点的下凸壳上的点可能成为最优决策点。

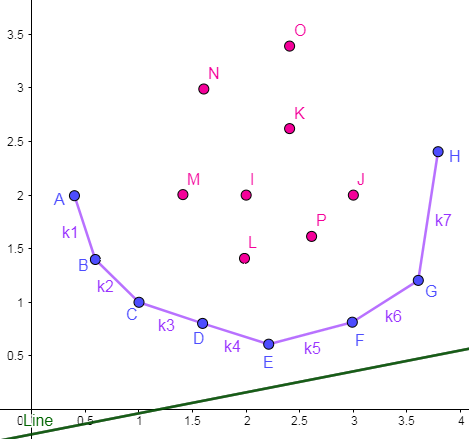
法二：代数法(数形结合)

设$j_1,j_2$ $(0\le j_1<j_2<i)$ 为$dp[i]$的两个决策点，且决策点$j_2$优于$j_1$，则有：
$A(i)\times B(j_2)+C(i)+D(j_2)\le A(i)\times B(j_1)+C(i)+D(j_1)$

化简式子，使不等号左边只与$i$有关，不等号右边只与$j_1,j_2$有关：
$A(i)\le -\frac{D(j_2)-D(j_1)}{B(j_2)-B(j_1)}$
$-A(i)\ge \frac{D(j_2)-D(j_1)}{B(j_2)-B(j_1)}$
设$x_j=B(j),y_j=D(j)$，则$\frac{D(j_2)-D(j_1)}{B(j_2)-B(j_1)}$可以看作$P_{j_1}(x_{j_1},y_{j_1})$,$P_{j_2}(x_{j_2},y_{j_2})$两点连线的斜率。

也就是说，如果存在两个决策点$j_1,j_2$满足$0\le j_1<j_2<i$，使得$P_{j_1}$,$P_{j_2}$两点连线的斜率$\le -A(i)$，那么决策点$j_2$优于$j_1$。

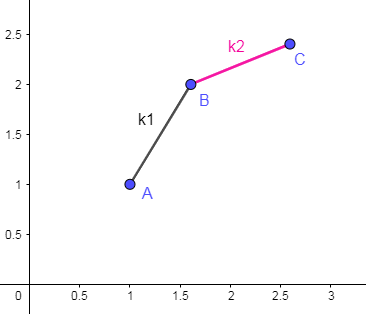
于是，对于这样子的三个点，可证$B$一定不是最优决策点。

我们可以将$B$从候选决策点中踢出去（删除），只留下$A$和$C$，删后的情况如下图所示：

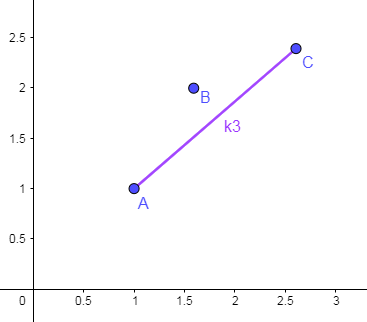
最终，我们维护的候选决策点应该构成了一个下凸壳：

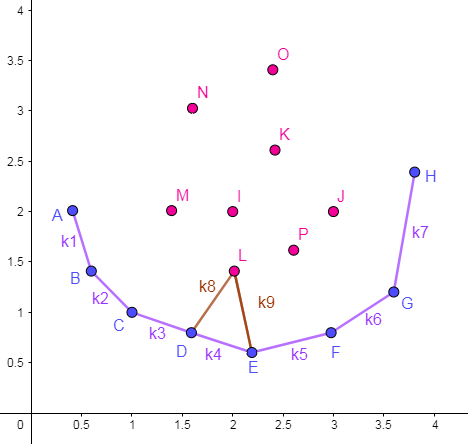
实现

按$x_j$的单调性分类

1. $x_j$递增（递减的话给$x$取个负就是递增了）：单调队列维护凸包
2. $x_j$不单调：平衡树维护凸包/cdq分治提供单调性

按$k_i$的单调性分类

1. $k_i$递增： 只需要维护部分凸包。即用单调队列维护凸包时可以不断弹掉队首，删掉不需要维护的凸包；查询答案时直接取队首即可。
2. $k_i$不递增：必须维护完整凸包。即用单调队列维护凸包时不能再弹掉队首了（即用单调栈维护凸包）；查询答案时二分找最优决策点。

实现细节

1. 当 $x_j$ 非严格递增时，在求斜率时可能会出现 $x_{j1}=x_{j2}$ 的情况，此时最好写成这样的形式：return Y(j)>=Y(i)?inf:-inf，而不要直接返回 $inf$ 或者 $-inf$
2. 手写队列的初始化是 h=1,t=0，由于队列初始化大多都要塞入一个点 $P(0)$，所以在一些题解中可以看到h=t=1
3. 手写队列判断不为空的条件是h<=t，而出入队判断都需要有至少 2 两个元素才能进行操作。所以应是 h<t 。
4. 计算斜率可能会因为向下取整而出现误差，所以 $slope$ 函数最好设为 $longdouble$ 类型。
5. 在比较两个斜率时，尽量写上等于，即<= 和 >= 而不是< 和>。这样写对于去重有奇效（有重点时会导致斜率分母出锅），但不要以为这样就可以完全去重，因为要考虑的情况可能会非常复杂，所以还是推荐加上 1. 中提到的特判，确保万无一失。