数据结构学习记录：第六章：树和二叉树-CSDN博客

本文链接：https://blog.csdn.net/Everybodynow/article/details/136226943

原文章：

数据结构学习记录：第六章：树和二叉树 - 知乎 (zhihu.com)

此文章为作者本人搬运至该网站。

说在前头：

各位在学习过程中，如果有任何不懂的地方，可以随时评论或者私信我！！！我每天都在高强度网上冲浪（这一点真的属实），从各位进行评论，到我发现评论，我认为应该最多不超过半个小时，所以啊，各位，尽情用你们的评论和私信淹没我吧！(=・ω・=)

1.树是什么：

树相比大家都很熟悉了吧！(￣3￣)

啊不对不对！不是这张图Σ(ﾟдﾟ;)，是这张！

树，是n(n>=0)个结点的有限集，而树的形象化表示如上面所示。每一个圆圈都是一个结点，而最上面的结点就叫做根节点。也就是说，根节点只有一个，在图里面就是最上面的A。

而树如果形象化来理解的话，其实就是一棵倒过来的树。而这棵树又可以分为许多子树，比如根节点A有三棵子树，也就是分别是以B、C、D为根的树，

而B也可以有两个子树，一个是以E为根的树，一个是以F为根的树（只有F这一个根结点的树）。

2.树的基本术语：

下面是树的一些基本术语，不过我觉得这些东西估计只会用在考试上面，而且这些东西虽然多，但是也比较简单，多看几遍就能理解：

(1).度：

树的某一结点所拥有的子树的数目，叫做该结点的度。

对上图来说，A结点有三个子树，那么A的度就是3。

而C结点有一个子树，那么C的度就是1，F结点没有子树，F的度就是0。

(2).叶子：

度为0的结点，就叫做叶子或者终端结点，或者叫叶子结点。像上面图中，K、L、F、G、M、I、J都是这个树的叶子。

(3).孩子和双亲：

对于一个结点来说，其子树的根叫做该节点的孩子，那么该结点就叫做孩子的双亲。

是不是感觉有点绕？其实简单来说，这个结点的上一层结点（两个结点用线连着）就是这个结点的双亲。

对！双亲其实就只有一个！！！( ´_ゝ｀)

而孩子其实就是这个结点的下一层结点（同样两个结点用线连着）。

图里面的话，对于结点B来说，A结点就是它的双亲，而E和F就是它的孩子。

而B结点下面的所有结点都可以叫做是B的子孙，这个也很简单。

(4).结点的层次：

其实在一开始的图里面已经展现过了，根节点为第一层，下面为第二层，以此类推。

而这个树里面最大的层次就是这个树的深度，上面那个图中，树的深度就是4。

(5).其他的：

有序树：树的各结点从左到右依次排序，最左边子树的根称为第一个孩子，最右边的称为最后一个孩子。

无序树：与有序树相反。

森林：许多互不相交的树的集合，也可以从字面意思来理解=w=。

而上面这些内容，我觉得都可以不用记，因为我们在之后的学习中也会频繁地使用这些名称。

而如果你觉得不自信的话，也可以试着做一下这个小测试：

(6)小测试：

最后一个堂兄弟也很简单拉，就是这个结点同一层的所有结点，但是不包括和自己同一个双亲的结点。

揭晓答案：

1.树的根是：A

2.树的叶子是：K, L, F, G, M, J, I

3.结点D的度：3

4.结点B的孩子是：E, F，子孙：E, F, K, L

5.树的度是：3，深度是：4

6.结点K的双亲是：E

7.结点F的堂兄弟是：G, H, J, I

3.二叉树的性质：

最有重量级的一集！

二叉树，顾名思义，就是每个结点最多只有两个孩子的树，而二叉树有以下5种基本形态：

图中结点的表示为圆圈，而叶子表示为近似半个八卦形状，但是其实两者从实际意义上来说也没有什么区别。

这里是几个知识点，考试的时候可能会出填空题选择题之类的。

(1).二叉树的第i层上面最多有 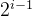$2^{i-1}$ 个结点(i >= 1)：

解释：如这个图所示，第1层的结点是1个， 20=1 ，

第2层的结点，由第1层的结点分成2个，共有2个， 21=2 ，

第3层的结点，由第2层的每个结点分别再分成2个，共有4个， 22=4 ，

以此类推。。。

(2).深度为k的二叉树最多有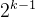 $2^{k-1}$ 个结点( k >= 1 )。

解释：如果把二叉树的每个结点都写上数字，如上图，从左到右，从上到下，那么到k层的时候，最右边的结点的数字就是 $2^{k-1}$ ，

第1层只有一个结点，最右边也就是那一个结点，数字为 $2^{1}$ −1=1 ，

第2层，最右边结点数字为 $2^{2}$ −1=4−1=3 ，

第3层，最右边结点数字为 $2^{3}$ −1=8−1=7 ，

以此类推。。。。

同时要注意！！！这一层最左边的结点数字是 2�−1 ！！！最右边的是2�−1，两者看似相像却又相隔甚远，一定不要写错了！！

如果记不住的话，可以自己写一遍二叉树，最左边的结点数字和最右边的结点数字就会清晰许多。

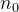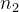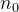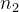(3).对任一棵二叉树，如果其终端结点（叶子）数为 $n_{0}$ ，度为2的结点数为 $n_{2}$ ，则 $n_{0}$ ＝ $n_{2}$ ＋1。

解释：终端结点（叶子结点），也就是没有孩子的结点，而度为2的结点，其实就是有两个孩子的结点，也就是说，没有孩子的结点的数目，就是有两个孩子结点的数目再加上1。

(4).具有n个结点的完全二叉树的深度为 $\left \lfloor\log _{2}n \right \rfloor + 1$ 。

注意！！！在这里出现了一个新名词：完全二叉树。

那这个第四点我们就按下不表，先去讲一下二叉树的种类。

4.二叉树的分类：

二叉树分为：满二叉树、完全二叉树和非完全二叉树（注意，这里的界限并不是完全分明的）

满二叉树：顾名思义，每个结点不是终端结点（叶子结点）就是有两个孩子的结点，整个二叉树的图看起来极其完美。

完全二叉树：其实如果光听名字的话，满二叉树和完全二叉树确实很容易混淆。大家还记得在上面讲二叉树的性质的内容我们是怎么讲的吗？

就是把每个结点都用一个数字标记，从上到下，从左到右依次递增，那么这样如果在数组里面存的话，就是从0递增，每个数字都有结点相对应，

（注意！！！这里我犯了个不明显的错误！！！树的图形表示里面，两个结点之间的连线是没有箭头的！！！我先入为主地给加上了后面也有很多有箭头的连线，大家注意！！！课本里面以及很多网上教程都是不带箭头的！！！）

这里不把数组第一个写成0是因为要和树的形式对齐。

但是当我们去掉6和4的时候，由于顺序都是从上到下，从左到右，那么这样数组就只能这样写：

这样就不是完全二叉树了，而叫做非完全二叉树。

也就是说，完全二叉树，必须要保证每个结点都是从左到右连续的，比如之前图中图b的样子：

还有这些，也是完全二叉树：

而以下的这些都是非完全二叉树（红色方框表示导致其为非完全二叉树的部分）：

这里最右边的那个结点缺失并不是该树成为非完全二叉树的原因

这样是不是比较清晰了？

同时要记得，一个树，不是完全二叉树就是非完全二叉树，

而满二叉树，满足完全二叉树的所有要求，那么它其实就是完全二叉树的一个特殊情况~

了解了完全二叉树后，我们再回来看那个二叉树的性质：

(4).具有n个结点的完全二叉树的深度为 $\left \lfloor\log _{2}n \right \rfloor + 1$ ：

大家别觉得有个log就是多么神奇的东西了，简单回想一下， $log_{2}n$ 是什么意思？

忘了？那么 $log_{2}2$ 呢？

其实就是求这个数是2的几次方。（我知道可能会有很多人觉得这个log还要讲？虽然但是，我是真的第一眼没看出来TAT）

还有一点就是，括住 $log_{2}n$ 的括号其实没有上面那一横！！！

不过还好课本已经给出了这个⌊x⌋负号的运算：

表示不大于x的最大整数。

而如果去掉下面一横

⌊x⌋

那就是表示不小于x的最小整数。

我们就这个满二叉树为例：

(4).具有n个结点的完全二叉树的深度为 $\left \lfloor\log _{2}n \right \rfloor + 1$ 。

这里n为15，那么

$\left \lfloor\log _{2}8 \right \rfloor$ =3< $\left \lfloor\log _{2}15 \right \rfloor$ < $\left \lfloor\log _{2}16 \right \rfloor$ =4

深度就是3+1=4，符合题目情况，

而如果是图b里面的完全二叉树，公式也是一样的，这里不过多细究。

5.二叉树的存储结构（定义二叉树）：

上面的那些内容都是填空题选择题会出的，但是如果是真正了解树是什么样的（并且是那种可以直接写成代码可以在oj上面跑的那种），还是要从二叉树的定义开始。

(1).顺序存储结构（数组）：

这里的存储方式其实就和我们用讲二叉树的性质时候用到的原理一样，数组按顺序从左到右，从上到下依次存储：

图中的树是这些数据的形象表达方式，而下面的数组才是数据存储在代码中真实的样子。

但是由于这个树是严格按照数组的方式进行顺序存储的，也就是说，图中数组T中的1，也就是第一个元素，就必须会在最上面的根结点的位置；数组T中的2，就必须要在第二层第一个元素的位置；数组T中的6，就必须在第三层中第三个元素的位置。

因为如果不这样做的话，我们以一个简化的树来举例：

这里是只有三个结点的二叉树，很明显，如果去掉右下角的那个3的结点的话，就会是这样：

但是如果是这样的话，数组又该怎么表示呢？

如果是两个元素一个1一个3的话，那么不就和上面的表示重复了么？

所以我们回过头来，二叉树的数组方法表示应该就可以理解了，那么这个树A的表示方法就是这样

其中'^'表示不存在此结点，课本中也用0进行表示，

这样就可以用独一无二的数组来表示这个独一无二的树了。

但是在这样的存储方法下，如果我们想要获得某个结点的数据，就必须要从数组头部开始遍历，而不能直接用数组序号访问，因为某些地方并没有结点，而数组会用^表示。

这样的话，显然没有结点的地方是根本不需要去访问的。在这里我们想象一个极端情况，所有的结点都在每一层的最右边（深度为k，且只有k个结点的二叉树）：

这样的话，如果用数组的情况表示的话，就需要创建长度为 2�−1 的数组，而里面有很多地方都是空结点，显然不利于存储。

那么我们该怎么办呢？

有没有发现图片中的树的表示里面每个结点之间，都是用箭头表示的？

那么就用到链式存储哒！(･∀･)

(2).链式存储结构：

链式存储，和链表一个道理，就是运用指针来指向结构体，在链表中，指针是指向下一个结构体，而二叉树的每个结点最多有两个孩子，那么其就应该有两个指针，分别指向左孩子和有孩子：

//----二叉树的二又链表存储表示----
typedef struct BiTNode {
	TElemType data;
	struct BiTNode *lchild，*rchild;	//左右孩子指针
} BiTNode，*BiTree;

而链式存储的结构如下表示：

图b是普通的二叉树的结点表示，也就是一个左孩子指针，一个右孩子指针，一个地方存储数据，

而图c则又加了个结点，就是指向双亲的指针，应该也很好理解，直接在 structBiTNode *lchild，*rchild; 后面加上个*parent即可。

这里用图片应该也能很好地展示每个结点的位置和功能（省得我再画图拉嘻嘻=w=）。

链式存储比顺序存储要好的一点就是前者可以节省大量内存空间，确保每一块开辟的空间都能用得上。

6.二叉树的先序遍历：

(1).遍历二叉树的思想：

按理说，这里应该讲二叉树的输入，输出，插入，删除之类的，

不过课本里面实在没有这些内容，而下面的内容也是考试的重点，所以我就先讲这个遍历二叉树了。

在这里推荐一下让我茅厕顿开的文章（雾）：

二叉树遍历方法——前、中、后序遍历（图解）_前序遍历-CSDN博客

这个文章真的很细致！！！里面几乎每一步都附带了图片，比我有耐心多了，我在有的时候也会因为懒得画图或者别的什么原因而不附带图，只是在这里干讲（这一点我也要注意了啊啊啊），我这里是从遍历原理开始讲的，可能会有些废话，如果想直接知道怎么遍历的可以看上面那个文章。

首先，我想问大家一个问题，

如果只用走两个结点之间的连线的方法，来从最上面的根节点走完所有的结点，且结点可以重复走过（废话，怎么可能一笔画完qwq），那么各位会选择什么样的走法？

还是以这棵树为例：

（写到这里我才发现我之前画的二叉树都是带有箭头的！这个问题我之前都没有想到！！！）

也就是说，从结点1，只可以走结点之间的连线，且可以重复走，直至把所有结点走完。

如果按照常规思维来想的话，很容易就能想到如下的走法：

从上到下，从左到右，

先从左边走到底，然后回头，找往右边走的路，最后的顺序是：

1->2->4->5->3->6->7

其中省略了重复走的结点，

如果各位在没了解二叉树的遍历之前，也是和我一样这样想的话，

那么，恭喜你！你已经实现了二叉树先序遍历的思维方法！！！(=・ω・=)

但是二叉树的遍历也有个要求，就是每个结点只能被访问一次（也就是一遍而过），那么该怎么实现呢？

这时候，递归就要派上用场了！！！

敲黑板！！！下面才是真正的重量级！！！

(2).先序遍历的操作步骤：

课本中，先序遍历二叉树的操作是这样定义的：

若二叉树为空，则空操作，否则：

①访问根节点；

②先序遍历左子树；

③先序遍历右子树。

在这里可能会有人不是很明白，因为没有附带代码，不过我相信就算贴上代码，各位也不一定看懂这个操作里面到底有几个小操作，那么各位可以先慢慢往下看，下面有个第一和第二，就是分别介绍前两个小操作的，而第③个操作，其实和第②个操作原理是一样的，这一点从之前对二叉树的定义就可以看出，左孩子和右孩子都是指针，只不过是名字不一样罢了。（#）

而这只是其中一步的操作，由于二叉树有很多结点，对每个结点都是这样操作的，那么就会进行数次。

既然有先序遍历，那就会有中序遍历和后序遍历，这两个遍历以及其和先序遍历的区别我们等会再讲。

我们按照这样的操作来对之前那个二叉树来进行实现：

首先，判断二叉树是否为空，很显然不为空，那么我们就开始操作：

第一，访问根节点：

注意！！！在这里，访问根节点只是个抽象的行为，而实际我们可以自定义对该结点的操作，比如输出该结点的数据等。

第二，先序遍历左子树：

子树子树，它是个树，而这里又提到了遍历，还记得我们一开始的操作叫做什么吗？

先序遍历！

那么在访问左子树里面，我们又要开始进行先序遍历的操作，也就是说，我们在进行先序遍历的操作的时候，需要在操作里面再进行一个先序遍历的操作。

这不就是递归的思想吗！

在调用这个函数的时候，调用的代码内容又要再次调用这个函数，而由于函数还是那个函数，所以会在再次调用函数的时候，里面的代码内容会第三次调用这个函数，直至对调用函数的判断不成立，后依次退出。

这个只是简单的回顾，如果各位对递归还不怎么熟悉的话，可以去搜一下相关内容，比如这些：

递归详解——让你真正明白递归的含义-CSDN博客

一文看懂什么递归（算法小结） - 知乎 (zhihu.com)

讲完了递归的大概思想，我们再回到二叉树这边，而其实把递归运用到二叉树里面也是比较容易理解的。

(3).递归，启动！

那么这边，其实所进行的操作已经很清晰了，对于上文中（#）的内容，其实这个算法的操作具体就有两个，一个是访问结点（输出数据），一个是遍历子树（左子树或者右子树），而我们这些过程，也就是不断进行这两个操作。

开始先序遍历左子树后，我们再开始进入先序遍历二叉树的操作：

也就是再次访问根节点，在这里，也就是左边第一个子树的根节点——2

访问完根节点后，再次先序遍历左子树，又是一次递归。

也就是走到4，对4进行访问，访问完之后，再次先序遍历4的左子树，

但是到这里，我们发现，4既没有左子树也没有右子树！！！

还记得我们访问根节点之前的步骤吗？

先对这个二叉树是否为空进行判断！！！

那么由于4的左子树为空，那么就进行空操作，

但是这里的操作还是基于对结点4的先序遍历左子树，也就是第②步操作，现在这个操作结束了（空操作），那么就要开始进行第③步，先序遍历右子树，

其实在这里，我们是第一次开始执行对右子树的先序遍历操作，我们可以先回顾一下之前的所有操作：

这里我用tab缩进来表示递归的次数，图中可以看出已经结束了第四次递归，

这样是不是清晰多了？(=・ω・=)

我们继续进行判断，此时开始遍历以4为结点的右子树，

而显然，右子树也为空树，那么这样的话也同样返回空操作。

此时，我们完成了第三次递归中，对以4为根结点的二叉树的三个操作，那么此时就结束了第三次递归，回到以2为根节点的二叉树的操作。

显然第三次递归的结束，也同样是了这个以2为根节点的二叉树的操作中第②个操作——先序遍历左子树的结束。此时进行第③个操作，先序遍历右子树，

也就是对以5为根节点的子树的操作，此时又进入一次递归。

就这样不断进行操作，直至所有子树都遍历完，那么就结束了对整个二叉树的遍历，这里我就不细写了。

那么这样，这个二叉树的先序遍历的访问结果就是：

1->2->4->5->3->6->7

和上面的常规思想做出来的一样！

(4).结合代码：

这里的内容已经多到让我加了好几个分割线了= =，不过我会把这一段独立成文章发出来的，毕竟这一段也挺重要的。

但是我猜还是会有一些人看不懂，或者说，懂了也不会用，那是因为咱还没切合代码来讲：

这里用到递归的函数就是PreOrderTraverse，但是里面的后面那个参数，也就是Status(*Visit)(TElemType e)，这个其实是指针函数，也就是说，函数名用指针指向，而注释里面也给出了Visit函数的一个例子，直接printf，

那么这个visit也就显而易见了，就是之前所说的访问根结点。

不过还要理解指针函数，多少也有点抽象，所以我在网上找了个比较好理解的：

//----二叉树的二又链表存储表示----
typedef struct BiTNode {
	TElemType data;
	struct BiTNode *lchild，*rchild;	//左右孩子指针
} BiTNode，*BiTree;

/*先序遍历*/
void PreOrder(BiTree T)
{
	if (T != NULL)
	{ 
		visit(T);              // 访问结点              
		PreOrder(T->lchild);   // 遍历结点左子树
		PreOrder(T->rchild);   // 遍历结点右子树
	}
}
 
/*输出树结点*/
void visit(BiTree T)
{
	printf("树结点的值：%c\n", T->data);
}

这个visit函数已经做到极简化了，只是为了让各位理解其本质(〜￣△￣)〜，

同时带上了二叉树的定义代码。

在这里递归的函数就成了PreOrder(T)，对于一开始的T——这个指针来说，它其实就是根节点的指针，而if语句里面的T->lchild，就是根结点的左孩子，同时也是二叉树根结点的左子树的根结点。

其余的原理也就和上面的内容差不多了。

(5).结合栈：

在这里，其实各位有没有意识到，其实递归的思想就和栈的思想差不多！

递归是从这个函数里面再进入这个函数，然后从进入的这个函数里面第二次进入这个函数，直到进入函数的条件不成立，之后则是从最后进入的函数出来，再从倒数第二个进入的函数再出来

是不是符合先进后出，后进先出？

数据结构学习记录：第三章：栈 - 知乎 (zhihu.com)

（忘了的话可以去补一下前面的文章哦=w=）

那么情况就很简单了，我们可以把上面遍历的过程用递归表示：

在这里，我们把PreOrder()这个函数当作对结点的入栈，当这个结点下面的if语句，一个访问根结点，以及又是两个PreOrder()的函数走完之后（或者直接if不成立），那么这个结点就出栈了，

我这样三言两语的可能讲不清楚，具体可以看这个文章：

二叉树遍历方法——前、中、后序遍历（图解）_前序遍历-CSDN博客

这是我第二次安利这个教程了，真的巨详细！！！

在这里我顺便放出文中的非递归版本的二叉树遍历：

//----二叉树的二又链表存储表示----
typedef struct BiTNode {
	TElemType data;
	struct BiTNode *lchild，*rchild;	//左右孩子指针
} BiTNode，*BiTree;

/*先序遍历*/
void PreOrder2(BiTree T)
{
	Stack S;		          // 申请一个辅助栈
	InitStack(&S);			  // 初始化
	BiTree p = T;			  // p为遍历指针
	while (p || !IsEmpty(S))  // 栈不为空或p不为空时循环
	{
		if (p)			      // 一路向左
		{
			visit(p);		  // 访问当前节点，并入栈
			Push(&S, p);
			p = p->lchild;	  // 左孩子不空，一直向左走
		}
		else				  //出栈，并转向出栈结点的右子树
		{
			Pop(&S, &p);	  // 栈顶元素出栈
			p = p->rchild;    // 向右子树走，p赋值为当前结点的右孩子
		}					  // 返回while循环继续进入if-else语句
	}
}

7.二叉树的中序遍历和后序遍历：

中序遍历，其实就和先序遍历差不多。

我一列出操作顺序各位应该就明白了：

若二叉树为空，则空操作，否则：

①中序遍历左子树；

②访问根节点；

③中序遍历右子树。

。。。

看清楚了吗？再看一遍先序遍历的操作：

若二叉树为空，则空操作，否则：

①访问根节点；

②先序遍历左子树；

③先序遍历右子树。

。。。

其实道理很简单，中序遍历，只不过是把访问根节点这个操作放在中间罢了。

什么？你问遍历左子树和右子树前面有个先序和中序的文字区别？

在我扎扎实实看了一遍内容后，我可以肯定地告诉你：

这个文字区别，仅仅是文字上的区别！！！

从先序的操作我们已经可以看出，这个遍历的操作只不过是又进入一次递归的函数罢了。

所以在这里我直接放出中序遍历的代码：

/*中序遍历*/
void InOrder(BiTree T)
{
	if (T != NULL)
	{
		InOrder(T->lchild);    // 遍历结点左子树
		visit(T);              // 访问结点
		InOrder(T->rchild);    // 遍历结点右子树
	}
}
 
/*输出树结点*/
void visit(BiTree T)
{
	printf("树结点的值：%c\n", T->data);
}

从代码里面我们也可以看出，其实先序中序后序遍历什么什么的，只不过是改变了访问根节点的顺序，以及函数名称而已，

实际上二叉树的遍历，一直是遵循从最上面的根节点，先左遍历到底，再一步一步往右边遍历，但是每一次往右边遍历后，都要再往左遍历！！！（易误解！！！）

而代码就留给各位了！各位也可以和我一样跟着代码的顺序一点一点画图并实现操作。

其实也不是因为我懒嘛（

主要是这几天感冒了一场，害得文章好久没更新，而且课程又落下好多，

另外，最最重要的是，

其实这三个遍历的内容我看上面那篇文章，用了二十分钟就看懂了，但是要真写出来教程的话，真的要花费不少心思。。。。

而且，这一部分都有比我更好更完善的教程了，我也不用再只用干涩的文字来讲拉～

在这里还是再推荐一下让我茅塞顿开的那篇文章：

二叉树遍历方法——前、中、后序遍历（图解）_前序遍历-CSDN博客

同时我也继续放出中序遍历和后续遍历的的代码：（中序遍历非递归）

/*中序遍历*/
void InOrder2(BiTree T)
{
	SqStack S;                  // 申请一个辅助栈
	InitStack(&S);				// 初始化
	BiTree p = T;				// p为遍历指针
	while (p || !IsEmpty(S))    // 栈不空或p不空时循环
	{
		if (p)					// 一路向左
		{
			Push(&S, p);        // 当前结点入栈
			p = p->lchild;		// 左孩子不空，一直向左走
		}
		else					// 出栈，并转向出栈结点的右子树
		{
			Pop(&S, &p);		// 栈顶元素出栈
			visit(p);			// 访问出栈结点
			p = p->rchild;		// 向右子树走，p赋值为当前结点的右孩子
		}						// 返回while循环继续进入if-else语句
	}
}

后序遍历：（递归版）

/*后序遍历*/
void PostOrder(BiTree T)
{
	if (T != NULL)
	{
		PostOrder(T->lchild);	// 遍历结点左子树
		PostOrder(T->rchild);	// 遍历结点右子树
		visit(T);				// 访问结点
	}
}
 
/*输出树结点*/
void visit(BiTree T)
{
	printf("树结点的值：%c\n", T->data);
}

后序遍历：（非递归）

/*后序遍历————利用标志*/
struct stack
{
	BiTree t;
	int tag;            // 标志
};						// tag = 0表示左子女被访问，tag = 1表示右字母被访问
void PostOrder3(BiTree T)
{
	struct stack s[Maxsize];
	int top = -1;
	while (T != NULL || top >= 0)
	{
		while (T != NULL)
		{
			s[++top].t = T;
			s[top].tag = 0;
			T = T->lchild;					// 沿左分支向下
		}
		while (top != -1 && s[top].tag == 1)
			visit(s[top--].t);					// 退栈
		if (top != -1)
		{
			s[top].tag = 1;						// 标志访问过右子树被访问
			T = s[top].t->rchild;				// 沿右分支向下遍历
		}
	}
}

8.根据遍历序列反推二叉树：

在二叉树的题目中，通过遍历序列反推二叉树是蛮重要的一部分，

而下面的这个文章是我新找到的，里面更清晰地展示了一种遍历二叉树的思维，大家可以看看，只不过我个人认为这里面的内容只有助于理解，做题肯定不能用这些方法：

数据结构——二叉树先序、中序、后序及层次四种遍历（C语言版）_中序遍历-CSDN博客

如果各位看了的话，就可以知道，里面的求中序遍历的序列是思想是：

中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果

但是这样要求二叉树的图必须足够准确，而现实情况往往做不到，

所以了解一下就行。

跑题了~还是上题目吧！

已知某二叉树前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }（访问根结点出来的结果），根据这两个序列构造二叉树。

在这里我们要知道的是，（重点！！！）

①.前序序列就是由先序遍历二叉树出来的结果，中序遍历同理；

②.由两种遍历序列便可以确定唯一二叉树；

③.前序序列的第一个字母，就是该二叉树的最上面的根节点；

④.中序序列的第一个字母，就是该二叉树的最左边的结点；

⑤.前序序列的第一个字母，在中序序列中，就意味着，在二叉树中，这个字母左边的字母都是在根节点左侧，而右边的字母都在根节点右侧。

这样一下子说出来各位可能不太好接受，我们通过这个题目一个一个来解释：

首先第一个就不用多说了，说辞的问题，不用太过追究；

第二个。。。。

很显然只凭一个序列肯定无法确定这个二叉树对吧！

第三个，

③.前序序列的第一个字母，就是该二叉树的最上面的根节点；

也很明显，我们再回顾一下先序遍历的操作：（怕各位忘记，我真贴心qwq）

若二叉树为空，则空操作，否则：

①访问根节点；

②先序遍历左子树；

③先序遍历右子树。

在这里，也就是先序遍历里面，访问根结点的操作在左遍历和右遍历之前，那么第一个访问的结点肯定就是最上面的根节点拉~

第四个，

④.中序序列的第一个字母，就是该二叉树的最左边的结点；

中序遍历的操作：

若二叉树为空，则空操作，否则：

①中序遍历左子树；

②访问根节点；

③中序遍历右子树。

可以看出，访问根节点的操作在左遍历之后，在右遍历之前，

那么中序遍历里面的第一次访问根结点的操作，肯定是在从二叉树中最上面的根结点往左边遍历到底后，访问最左边最底下的那个结点。

所以，中序遍历中，第一个访问的结点肯定是最左边的这个结点。

第五个，

⑤.前序序列的第一个字母，在中序序列中，就意味着，在二叉树中，这个字母左边的字母都是在根节点左侧，而右边的字母都在根节点右侧。

这个可以说是我通过做题总结出的小技巧，我们拿这个简单的树来举例子：

请各位先写出这个树的先序、中序和后序遍历：（如果还是不熟练的各位可以对着遍历的操作一步一步走，遍历结果其实就是访问根结点的顺序）

。。。

答案揭晓：

先序：ABDECFG

中序：DBEAFCG

后序：DEBFGCA

这一步真心建议各位用纸和笔自己演算一遍！！！

如果真的上手算了，各位就会知道为什么中序遍历中的A会在DBE的右边，FCG的左边了。

那么我们再回到原来那个题：

已知某二叉树前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }（访问根结点出来的结果），根据这两个序列构造二叉树。

那么就可以分为以下几个步骤：

①.先看前序序列的头部，是A，那么这个二叉树最上面的根结点就是A；

②.看A在中序序列中的位置，那么这个二叉树中，HBDF就在A的左边，EKCG在A的右边，

目前情况如图：

HBDF目前可以确定是在A的左子树里，但是它们内部的顺序还不清晰，那么就先这样写，

右边的EKCG同理。

③.再次回到前序序列（毕竟我们对这个了解最多），找到关于A的左子树里面HBDF的顺序，

是BHFD，

而由于先序遍历肯定是先一直走到左下的，所以我们需要：

④.看中序序列中的头部，是H，那么先序遍历中左边一直遍历就会走到H而停下（也就是说H会在这个二叉树最左边的位置），再结合前序序列中的BHFD的顺序，就可以得出，

这个二叉树的左边一条直线的顺序是：A->B->H：

那么A的左子树部分只剩下D和F没有确定了，

我们再回到题目的前序序列：{ ABHFDECKG }

F在D前面，

可以确定的是F在上面，而D是F的一个子树，

但是究竟是左子树还是右子树呢？

既然只有两种可能，那么我们不妨假设一下？

⑤.假设D是F的左子树：

我们再结合中序序列：{ HBDFAEKCG }

中序序列是左遍历结束后再访问根结点，而在这里D是在F前面，

也就是说，在B的右遍历里，F左遍历，再到D，（这里可以再根据中序遍历的操作推导一遍）

那么中序遍历中D和F，先访问的根结点就是D！！！

假设成立！！！

那么在这里，A的左边的顺序就很清楚了，我们开始看右边的EKCG。

⑥.我们把已经排好顺序的字母去掉，可以得出：

前序序列：ECKG

中序序列：EKCG

两个序列的E是一样的，那么很显然E是在A的左子树的根结点的位置：

而剩下三个字母的位置的判断，方法是相通的，同时我们也可以多运用假设法，毕竟二叉树，子树不是在左边就是在右边嘛~

最后可以得出这个结果：

你答对了吗_(:з」∠)_

再给大家自己思考一个题：

先序序列：A B D H I E J C F K G

中序序列：H D I B E J A F K C G

画出这个二叉树。

由于字母比较多，可能会有点复杂，也建议拿笔和纸自己演算一遍！！！

答案：

先写到这里，后续内容可以先点个收藏等更新~

本文章持续更新~~

数据结构学习记录：第六章：树和二叉树

原文章：

说在前头：

1.树是什么：

2.树的基本术语：

(1).度：

(2).叶子：

(3).孩子和双亲：

(4).结点的层次：

(5).其他的：

3.二叉树的性质：

(1).二叉树的第i层上面最多有 个结点(i >= 1)：

(2).深度为k的二叉树最多有 个结点( k >= 1 )。

(3).对任一棵二叉树，如果其终端结点（叶子）数为 ，度为2的结点数为 ，则＝＋1。

(4).具有n个结点的完全二叉树的深度为 。

4.二叉树的分类：

(4).具有n个结点的完全二叉树的深度为：

5.二叉树的存储结构（定义二叉树）：

(1).顺序存储结构（数组）：

(2).链式存储结构：

6.二叉树的先序遍历：

(1).遍历二叉树的思想：

(2).先序遍历的操作步骤：

(3).递归，启动！

(4).结合代码：

(5).结合栈：

7.二叉树的中序遍历和后序遍历：

8.根据遍历序列反推二叉树：

(1).二叉树的第i层上面最多有 $2^{i-1}$ 个结点(i >= 1)：

(2).深度为k的二叉树最多有 $2^{k-1}$ 个结点( k >= 1 )。

(3).对任一棵二叉树，如果其终端结点（叶子）数为 $n_{0}$ ，度为2的结点数为 $n_{2}$ ，则 $n_{0}$ ＝ $n_{2}$ ＋1。

(4).具有n个结点的完全二叉树的深度为 $\left \lfloor\log _{2}n \right \rfloor + 1$ 。

(4).具有n个结点的完全二叉树的深度为 $\left \lfloor\log _{2}n \right \rfloor + 1$ ：