Codeforce 479div3 E题 —图论

E. Cyclic Components

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$, a vertex $b$ is also connected with a vertex $a$). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$.

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

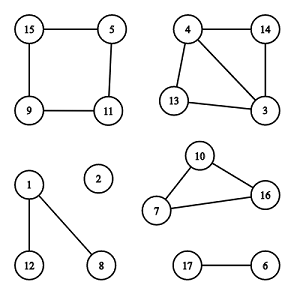There are $6$ connected components, $2$ of them are cycles: $[7,10,16]$ and $[5,11,9,15]$.

Input

The first line contains two integer numbers $n$ and $m$ ($1\le n\le 2\cdot {10}^5$, $0\le m\le 2\cdot {10}^5$) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_i$, $u_i$ ($1\le v_i,u_i\le n$, $u_i\ne v_i$). There is no multiple edges in the given graph, i.e. for each pair ($v_i,u_i$) there no other pairs ($v_i,u_i$) and ($u_i,v_i$) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Examples

input

Copy

5 4
1 2
3 4
5 4
3 5

output

Copy

1

input

Copy

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

output

Copy

2

Note

In the first example only component $[3,4,5]$ is also a cycle.

The illustration above corresponds to the second example.

挺水的一道图论，当时自己也不知道在想什么。。没做出来。心态爆炸，后来想想，看了一下题解。发现就是搜度为2的点，而且能凑成一个环，用vector存图，用dfs遍历一遍就行了，用一个flag做标记

#include<bits/stdc++.h>
using namespace std;
const int maxn=200050;
vector<int>vec[maxn];   //存图 
bool vis[maxn];   //标记 
int flag,ans;
void dfs(int n)
{
	if(vis[n])    //搜索到走过的边，返回 
	{
		return ;
	}
	if(vec[n].size()!=2)   //存在环里有点不满足度为2的条件 
	{
		flag=1;
	}
	vis[n]=true;
	for(int i=0;i<vec[n].size();i++)
	{
		dfs(vec[n][i]);    
	}
}
int main()
{
	//freopen("C:/input.txt", "r", stdin);
	int n,m;
	memset(vis,false,sizeof(vis));
	scanf("%d%d",&n,&m);
	for(int i=0;i<m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		vec[u].push_back(v);
		vec[v].push_back(u);
	}
	ans=0;
	for(int i=1;i<=n;i++)    //遍历所有的点 
	{
		if(!vis[i])
		{
			flag=0;
			dfs(i);
			if(flag==0)     //满足构成环的点的度数都为2，计数器加1 
			{
				ans++;
			}
		}
	}
	printf("%d\n",ans);
	return 0;		
}