1 引言
哈夫曼(Huffman)编码算法是基于二叉树构建编码压缩结构的,它是数据压缩中经典的一种算法。算法根据文本字符出现的频率,重新对字符进行编码。因为为了缩短编码的长度,我们自然希望频率越高的词,编码越短,这样最终才能最大化压缩存储文本数据的空间。
假设现在我们要对下面这句歌词“we will we will r u”进行压缩。我们可以想象,如果是使用ASCII码对这句话编码结果则为:119 101 32 119 105 108 108 32 119 101 32 119 105 108 108 32 114 32 117(十进制表示)。我们可以看出需要19个字节,也就是至少需要152位的内存空间去存储这些数据。
很显然直接ASCII码编码是很浪费空间的,Unicode就更不用说了,下面我们先来统计一下这句话中每个字符出现的频率。如下表,按频率高低已排序:

2 哈夫曼二叉树构建
2.1 初始队列
那么我们按出现频率高低将其放入一个优先级队列中,从左到右依次为频率逐渐增加。

下面我们需要将这个队列转换成哈夫曼二叉树,哈夫曼二叉树是一颗带权重的二叉树,权重是由队列中每个字符出现的次数所决定的。并且哈夫曼二叉树始终保证权重越大的字符出现在越高的地方。
2.2 第一步合并
首先我们从左到右进行合并,依次构建二叉树。第一步取前两个字符u和r来构造初始二叉树,第一个字符作为左节点,第二个元素作为右节点,然后两个元素相加作为新空元素,并且两者权重相加作为新元素的权重。
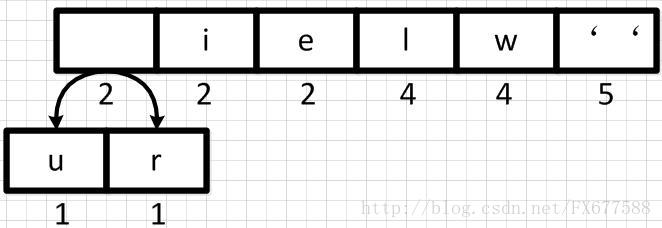
同理,新元素可以和字符i再合并,如下:
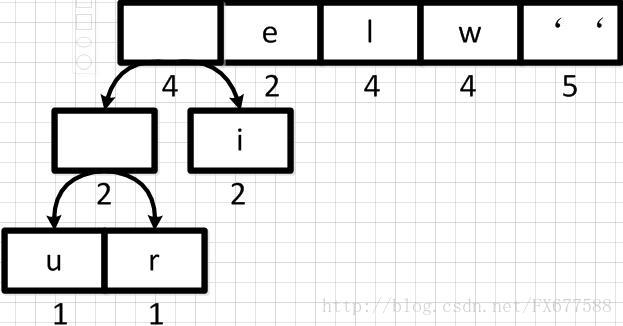
2.3 重新调整队列
上图新元素权重相加后结果是变大了,需要对权重进行重新排序。
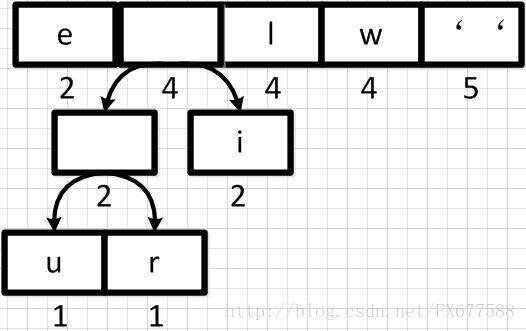
然后再依次从左到右合并,每合并一次则进行一次队列重新排序调整。如下:
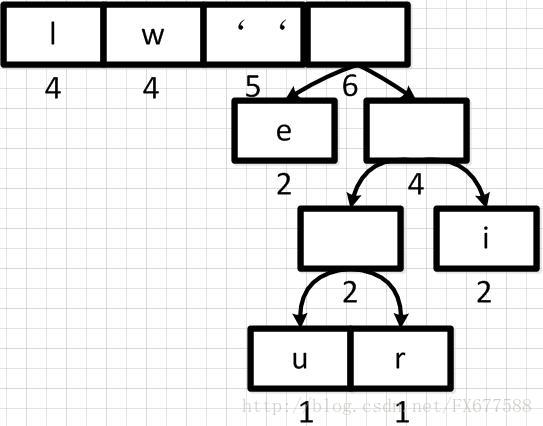
经过多步操作之后,得到以下的哈夫曼二叉树结构,也就是一个带有权重的二叉树:
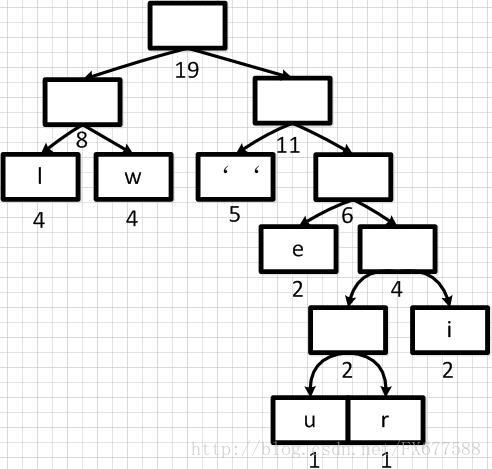
2.4 哈夫曼编码
有了上面带权重的二叉树之后,我们就可以进行编码了。我们把二叉树分支中左边的支路编码为0,右边分支表示为1,如下图:
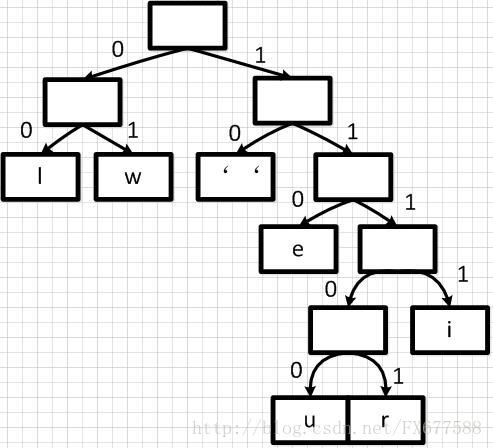
这样依次遍历这颗二叉树就可以获取得到所有字符的编码了。例如:‘ ’的编码为10,‘l’的编码为00,‘u’的编码为11100等等。经过这个编码设置之后我们可以发现,出现频率越高的字符越会在上层,这样它的编码越短;出现频率越低的字符越会在下层,编码越短。经过这样的设计,最终整个文本存储空间才会最大化的缩减。
最终我们可以得到下面这张编码表:

2.5 字符串编码
有了上面的编码表之后,”we will we will r u”这句重新进行编码就可以得到很大的压缩,编码表示为:01 110 10 01 1111 00 00 10 01 110 10 01 1111 00 00 10 11101 10 11100。这样最终我们只需50位内存,比原ASCII码表示节约了2/3空间,效果还是很理想的。当然现实中不是简单这样表示的,还需要考虑很多问题。
3 补充
我们需要弄明白哈夫曼二叉树概念,它是带权路径达到最小的二叉树,也叫最优二叉树。它不一定是完全二叉树,也不一定是平衡二叉树,它们描述的完全不是一件事情,完全没有概念上的重叠关系。
个人学习记录,由于能力和时间有限,如果有错误望读者纠正,谢谢!
转载请注明出处:http://blog.csdn.net/fx677588/article/details/70767446





















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








