1564: [NOI2009]二叉查找树
Time Limit: 10 Sec Memory Limit: 64 MB
Submit: 705 Solved: 498
[Submit][Status][Discuss]
Description
Input
Output
只有一个数字,即你所能得到的整棵树的访问代价与额外修改代价之和的最小值。
Sample Input
4 10
1 2 3 4
1 2 3 4
1 2 3 4
Sample Output
29
HINT
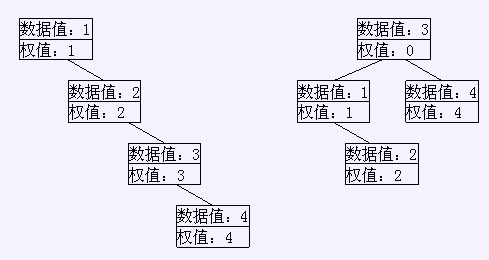
输入的原图是左图,它的访问代价是1×1+2×2+3×3+4×4=30。最佳的修改方案是把输入中的第3个结点的权值改成0,得到右图,访问代价是1×2+2×3+3×1+4×2=19,加上额外修改代价10,一共是29。
无论权值怎样改变,按照数据值进行中序遍历后的序列肯定的不变的。
所以就可以变成在数列上进行
dp
了。
题目中说的修改的权值可以是实数,也就是说可以不管哪个权值可以不同的限制了。
设
f[i][j][k]
表示在
i,j
这个子树内,所有节点权值大于等于
k
的最小代价。
转移的时候可以枚举这个子树的根,然后用左右两端加上这个根拼成这个子树。这样就相当于所有节点的深度都加了
注意在当前根的权值大于等于
k
的时候,还要再加上一个没有修改根权值的操作的转移。
复杂度:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define inf 0x7fffffff
const int N=100;
struct Point{int key,v,p;}p[N];
int n,K,f[N][N][N],a[N],sum[N];
inline bool cmp(Point x,Point y){return x.key<y.key;}
int main(){
int i,j,k,q;
scanf("%d%d",&n,&K);
for(i=1;i<=n;++i) scanf("%d",&p[i].key);
for(i=1;i<=n;++i) scanf("%d",&p[i].v);
for(i=1;i<=n;++i) scanf("%d",&p[i].p);
sort(p+1,p+n+1,cmp);
for(i=1;i<=n;++i) a[i]=p[i].v;
sort(a+1,a+n+1);
for(i=1;i<=n;++i){
sum[i]=sum[i-1]+p[i].p;
p[i].v=lower_bound(a+1,a+n+1,p[i].v)-a;
}
memset(f,127,sizeof(f));
for(i=1;i<=n+1;++i)
for(j=0;j<=n;++j) f[i][i-1][j]=0;
for(i=1;i<=n;++i)
for(j=0;j<=n;++j)
f[i][i][j]=p[i].p+((p[i].v>=j)?0:K);
for(k=1;k<n;++k)
for(i=1;i+k<=n;++i)
for(j=0;j<=n;++j)
for(q=i;q<=i+k;++q){
f[i][i+k][j]=min(f[i][i+k][j],f[i][q-1][j]+f[q+1][i+k][j]+K+sum[i+k]-sum[i-1]);
if(p[q].v>=j)
f[i][i+k][j]=min(f[i][i+k][j],f[i][q-1][p[q].v]+f[q+1][i+k][p[q].v]+sum[i+k]-sum[i-1]);
}
printf("%d\n",f[1][n][0]);
}























 222
222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








