墓地雕塑（Graveyard, NEERC 2006, LA 3708）

墓地雕塑（Graveyard, NEERC 2006, LA 3708）

　　在一个周长为10000的圆上等距分布着n个雕塑。现在又有m个新雕塑加入（位置可以随意放），希望所有n+m个雕塑在圆周上均匀分布。这就需要移动其中一些原有的雕塑。要求n个雕塑移动的总距离尽量小。
【输入格式】
　　输入包含若干组数据。每组数据仅一行，包含两个整数n和m（2≤n≤1 000，1≤m ≤1 000），即原始的雕塑数量和新加的雕塑数量。输入结束标志为文件结束符（EOF）。
【输出格式】
　　输入仅一行，为最小总距离，精确到10-4。
【样例输入】

2 1
2 3
3 1
10 10

【样例输出】

1666.6667
1000.0
1666.6667
0.0

【样例解释】
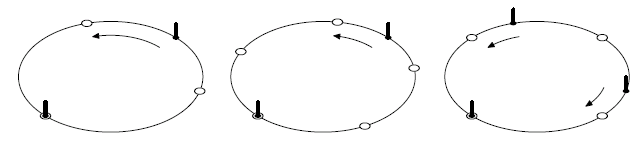
　　前3个样例如图所示。白色空心点表示等距点，黑色线段表示已有雕塑。

分析1：

　　请仔细看看样例。3个样例具有一个共同的特点：有一个雕塑没有移动。如果该特点在所有情况下都成立，则所有雕塑的最终位置（称为“目标点”）实际上已经确定。为了简单起见，我们把没动的那个雕塑作为坐标原点，其他雕塑按照逆时针顺序标上到原点的距离标号，如图所示。

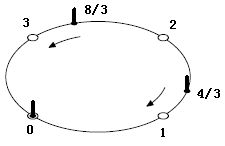
　　注意，这里的距离并不是真实距离，而是按比例缩小以后的距离。接下来，我们把每个雕塑移动到离它最近的位置。如果没有两个雕像移到相同的位置，那么这样的移动一定是最优的。

代码1：

#include<cstdio>
#include<cmath>
using namespace std;

int main() {
  int n, m;
  while(scanf("%d%d", &n, &m) == 2) {
    double ans = 0.0;
    for(int i = 1; i < n; i++) {
      double pos = (double)i / n * (n+m);       //计算每个需要移动的雕塑的坐标
      ans += fabs(pos - floor(pos+0.5)) / (n+m);    //累加移动距离
    }
    printf("%.4lf\n", ans*10000);               //等比例扩大坐标
  }
  return 0;
}

　　注意在代码中，坐标为pos的雕塑移动到的目标位置是floor(pos+0.5)，也就是pos四舍五入后的结果。这就是坐标缩小的好处。
　　这个代码很神奇地通过了测试，但其实这个算法有两个小小的“漏洞”：首先，我们不知道是不是一定有一个雕塑没有移动；其次，我们不知道会不会有两个雕塑会移动到相同的位置。如果你对证明不感兴趣，或者已经想到了证明，再或者迫不及待地想阅读更有趣的问题，请直接跳到下一个例题。否则，请继续阅读。
第一个“漏洞”的修补需要证明我们的猜想。证明思路在例题3中我们已经展示过了，具体的细节留给读者思考。
　　第二个“漏洞”有两种修补方法。第一种方法相对较容易实施：由于题目中规定了n,m≤1 000，我们只需要在程序里加入一个功能——记录每座雕塑移到的目标位置，就可以用程序判断是否会出现“人多坑少”的情况。这段程序的编写留给读者，这里可以明确地告诉大家：这样的情况确实不会出现。这样，即使无法从理论上证明，也可以确保在题目规定的范围内，我们的算法是严密的。
　　第二种方法就是直接证明。在我们的程序中，当坐标系缩放之后，坐标为x的雕塑被移到了x四舍五入后的位置。如果有两个坐标分别为x和y的雕塑被移到了同一个位置，说明x和y四舍五入后的结果相同，换句话说，即x和y“很接近”。至于有多接近呢？差距最大的情况不外乎类似于x=0.5, y=1.499 999…。即便是这样的情况，y-x仍然小于1（尽管很接近1），但这是不可能的，因为新增雕塑之后，相邻雕塑的距离才等于1，之前的雕塑数目更少，距离应当更大才对。

令笔者引以为傲的分析2：

代码2：

#include <cstdio>
#include <string.h>
#include <math.h>
#include <stdlib.h>
using namespace std;

int Around(double z)
{
    if(z-(int)z >= 0.5)
        return (int)(z + 1);
    else
        return (int)z;
}

double a[1000], b[1000];
double L = 10000;  //圆的周长
double S;  //移动的总距离

int main()
{
    int n, m;
    int i;
    while (scanf("%d %d", &n, &m) == 2)
    {
        double r = (double)(n+m)/n;
        S = 0;
        a[0] = 0;
        b[0] = 0;
        for(i = 1; i < n; i++)
        {
            a[i] = a[i-1] + L/n;
        }
        for(i = 1; i < n+m; i++)
        {
            b[i] = b[i-1] + L/(n+m);
        }

//        for(i = 0; i < n; i++)
//        {
//            printf("%lf ", a[i]);
//        }printf("\n");
//        for(i = 0; i < n+m; i++)
//        {
//            printf("%lf ", b[i]);
//        }printf("\n");
//        printf("%lf\n", r);

        for(i = 1; i < n; i++)
        {
            S = S + fabs(a[i] - b[Around(i*r)]);  //printf("%d ", Around(i*r)); printf("%f ", S);
        }                                         //printf("\n");
        printf("%.4lf\n", S);
    }
    return 0;
}