CEC2013-benchmark基准测试函数及代码

可以用CEC13BenchMark来测试自己的算法。

20个具有不同特征的基准测试函数（包括几个相同但尺寸大小不同的函数）来评估小生境算法

函数

• $F_1:$Five-Uneven-Peak Trap (1D)
• $F_2:$Equal Maxima (1D)
• $F_3:$Uneven Decreasing Maxima (1D)
• $F_4:$Himmelblau (2D)
• $F_5:$Six-Hump Camel Back (2D)
• $F_6:$Shubert (2D,3D)
• $F_7:$Vincent (2D,3D)
• $F_8:$Modified rastrigin - All Global Optima (2D)
• $F_9:$Composition Function 1 (2D)
• $F_{10}:$Composition Function 2 (2D)
• $F_{11}:$Composition Function 3 (2D,3d,5D,10D)
• $F_{12}:$Composition Function 4 (3D,5d,10D,20D)

公式

• $F_1:$Five-Uneven-Peak Trap (1D)

  • $$F_i=\{\begin{array}{ll}80(2.5-x)& for0⩽x<2.5\\ 64(x-2.5)& for2.5⩽x<5.0\\ 64(7.5-x)& for5.0⩽x<7.5\\ 28(x-7.5)& for7.5⩽x<12.5\\ 28(17.5-x)& for12.5⩽x<17.5\\ 32(x-17.5)& for17.5⩽x<22.5\\ 32(27.5-x)& for22.5⩽x<27.5\\ 80(x-27.5)& for27.5⩽x<30\end{array}$$

  • $xϵ[0,30]$

• $F_2:$Equal Maxima (1D)

  • $$F_2(x)={\sin }^6(5\pi x)$$

  • $xϵ[0,1]$

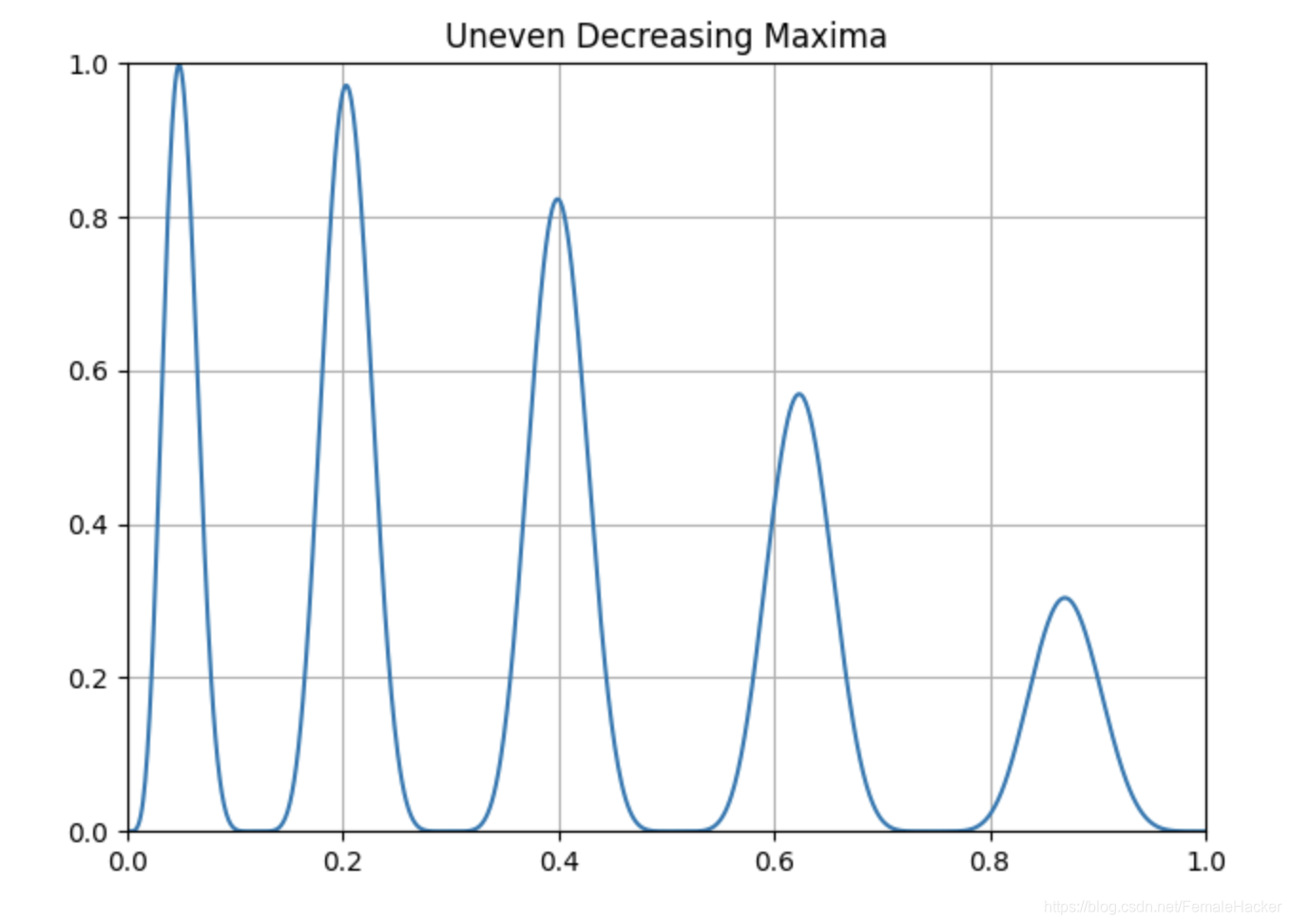
• $F_3:$Uneven Decreasing Maxima (1D)

  • $$F_3(x)=\exp (-2\log (2)(\frac{x-0.08}{0.854}{)}^2){\sin }^6(5\pi (x^{3/4}-0.05))$$

  • $xϵ[0,1]$

• $F_4:$Himmelblau (2D)

  • $$F_4(x,y)=200-(x^2+y-11{)}^2-(x+y^2-7{)}^2$$

  • $xϵ[-6,6]$

• $F_5:$Six-Hump Camel Back (2D)

  • $$F_5(x,y)=-4[(4-2.1x^2+\frac{x^4}{3})x^2+xy+(4y^2-4)y^2]$$

  • $xϵ[-1.9,1.9]$$yϵ[-1.1,1.1]$

• $F_6:$Shubert (2D,3D)

  • $$F_6(\vec{x})=-\prod _{i=1}^D\sum _{j=1}^{5}j\cos [(j+1)x_i+j]$$

  • $x_iϵ[-10,10{]}^D,i=1,2,...,D$

• $F_7:$Vincent (2D,3D)

  • $$F_7(\vec{x})=\frac{1}{D}\sum _{i=1}^D\sin (10\log (x_i))$$

  • $x_iϵ[0.25,10{]}^D,i=1,2,...,D$

• $F_8:$Modified rastrigin - All Global Optima (2D)

  • $$F_9(\vec{x})=-\sum _{i=1}^D(10+9\cos (2\pi k_i{x}_i))$$

  • $x_iϵ[0,1{]}^D,i=1,2,...,D$

• $F_9:$Composition Function 1 (2D)

  • 6个函数组成

  • f1-f2:Grienwank’s Function f3-f4:Weierstrass function f5-f6:Sphere function

  • A D = [ − 5 , 5 ] D σ i = 1 , ∀ i ϵ { 1 , 2 , . . . , n } λ = [ 1 , 1 , 8 , 8 , 1 / 5 , 1 / 5 ] A_D=[-5,5]^D \\ \sigma_i = 1,\forall_i \epsilon{\{1,2,...,n}\}\\ \lambda = [1,1,8,8,1/5,1/5] AD​=[−5,5]Dσi​=1,∀i​ϵ{1,2,...,n}λ=[1,1,8,8,1/5,1/5]

• $F_{10}:$Composition Function 2 (2D)

  • 8个函数组成

  • f1-f2:Restigin’s function f3-f4:Weierstrass function f5-f6:Grienwank’s Function f7-f8:Sphere function

  • A D = [ − 5 , 5 ] D σ i = 1 , ∀ i ϵ { 1 , 2 , . . . , n } λ = [ 1 , 1 , 10 , 10 , 1 / 10 , 1 / 10 , 1 / 7 , 1 / 7 ] A_D=[-5,5]^D \\ \sigma_i = 1,\forall_i \epsilon{\{1,2,...,n}\}\\ \lambda = [1,1,10,10,1/10,1/10,1/7,1/7] AD​=[−5,5]Dσi​=1,∀i​ϵ{1,2,...,n}λ=[1,1,10,10,1/10,1/10,1/7,1/7]

• $F_{11}:$Composition Function 3 (2D,3d,5D,10D)

  • 6个函数组成

  • f1-f2:EF8F2 function f3-f4:Weierstrass function f5-f6:Grienwank’s Function

  • $$\begin{gathered} A_D=[-5,5{]}^D \\ {\sigma }_i=[1,1,2,2,2,2] \\ \lambda =[1/4,1/10,1,2,5] \end{gathered}$$

• $F_{12}:$Composition Function 4 (3D,5d,10D,20D)

  • 8个函数组成

  • f1-f2:Restigin’s function f3-f4:EF8F function f5-f6:Weierstrass function f7-f8:Grienwank’s Function

  • $$\begin{gathered} A_D=[-5,5{]}^D \\ {\sigma }_i=[1,1,1,1,1,2,2,2] \\ \lambda =[4,1,4,1,1/10,1/5,1/10,1/40] \end{gathered}$$

  ---

• Sphere function

  • $$f_S(\vec{x})=\sum _{i=1}^D{x}_i^2$$

• Grienwank’s function

  • $$f_G(\vec{x})=\sum _{i=1}^D\frac{x_i^2}{4000}-\prod _{i=1}^D\cos (\frac{x_i}{\sqrt{i}})+1$$

• Restrigin’s function

  • $$f_R(\vec{x})=\sum _{i=1}^D(x_i^2-10\cos (2\pi x_i)+10)$$

• Weierstrass function

  • $$\begin{gathered} f_W(\vec{x})=\sum _{i=1}^D(\sum _{k=0}^{kmax}{\alpha }^k\cos (2\pi {\beta }^k(x_i+0.5)))-D\sum _{k=0}^{kmax}{\alpha }^k\cos (2\pi {\beta }^k(0.5)) \\ \alpha =0.5,\beta =3,kmax=20 \end{gathered}$$

• Expanded Griewank’s plus Rosenbrock’s function(EF8F2)

  • $$\begin{gathered} F8(\vec{x})=\sum _{i=1}^D\frac{x_i^2}{4000}-\prod _{i=1}^D\cos (\frac{x_i}{\sqrt{i}})+1 \\ F2(\vec{x})=\sum _{i=1}^D(100(x_i^2-x_{i+1}{)}^2)+(x_i-1{)}^2 \\ EF8F2(\vec{x})=F8F2(x_1,x_2,...,x_D)=F8(F2(x_1,x_2))+F8(F2(x_2,x_3))+...+F8(F2(x_{D-1},x_D))+F8(F2(x_D,x_1)) \end{gathered}$$

python绘制基准测试函数

最近在学正好就绘制了一下

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def draw_pic(x, y, title, x_min, x_max, y_min, y_max):
    plt.grid(True)  ##增加格点
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.title(title)
    plt.plot(x, y)
    plt.show()


def draw_pic_3D(x, y, z, title, z_min, z_max, offset):
    fig = plt.figure()
    ax = Axes3D(fig)
    # rstride代表row行步长  cstride代表colum列步长  camp 渐变颜色
    ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap = plt.get_cmap('rainbow'),color='orangered')
    # 绘制等高线
    ax.contour(x,y,z,offset=offset,colors='green')
    ax.set_zlim(z_min, z_max)
    ax.set_title(title)
    plt.show()


def get_x_and_y(x_min, x_max, y_min, y_max):
    x = np.arange(x_min, x_max, 0.1)
    y = np.arange(y_min, y_max, 0.1)
    x, y = np.meshgrid(x, y)  # 生成网格点坐标矩阵
    return x, y


# 1
def Five_uneven_peak_Trap(x_min=0, x_max=30, y_min=0, y_max=200):
    x = np.linspace(0, 30, 1000)

    interval0 = [1 if (i >= 0.0) & (i < 2.5) else 0 for i in x]
    interval1 = [1 if (i >= 2.5) & (i < 5.0) else 0 for i in x]
    interval2 = [1 if (i >= 5.0) & (i < 7.5) else 0 for i in x]
    interval3 = [1 if (i >= 7.5) & (i < 12.5) else 0 for i in x]
    interval4 = [1 if (i >= 12.5) & (i < 17.5) else 0 for i in x]
    interval5 = [1 if (i >= 17.5) & (i < 22.5) else 0 for i in x]
    interval6 = [1 if (i >= 22.5) & (i < 27.5) else 0 for i in x]
    interval7 = [1 if (i >= 27.5) & (i < 30.0) else 0 for i in x]

    y = 80 * (2.5 - x) * interval0 + 64 * (x - 2.5) * interval1 + 64 * (7.5 - x) * interval2 + 28 * (
            x - 7.5) * interval3 + 28 * (17.5 - x) * interval4 + 32 * (x - 17.5) * interval5 + 32 * (
                27.5 - x) * interval6 + 80 * (x - 27.5) * interval7
    return x, y, 'Five-Uneven-Peak Trap', x_min, x_max, y_min, y_max


# 2
def Equal_maxima(x_min=0, x_max=1, y_min=0, y_max=1):
    x = np.linspace(0, 1, 1000)
    y = np.sin(5 * np.pi * x) ** 6
    return x, y, 'Equal Maxima', x_min, x_max, y_min, y_max


# 3
def Uneven_decreasing_maxima(x_min=0, x_max=1, y_min=0, y_max=1):
    x = np.linspace(0, 1, 1000)
    y = np.exp(-2 * np.log(2) * ((x - 0.08) / 0.854) ** 2) * (np.sin(5 * np.pi * (x ** (3 / 4)) - 0.05)) ** 6
    return x, y, 'Uneven Decreasing Maxima', x_min, x_max, y_min, y_max


# 4
def Himmelblau(z_min=-2000, z_max=0, offset=-2000):
    x, y = get_x_and_y(-6, 6, -6, 6)
    z = 200 - (x ** 2 + y - 11) ** 2 - (x + y ** 2 - 7) ** 2
    return x, y, z, 'Himmelblau', z_min, z_max, offset


# 5
def Six_hump_camel_back(z_min=-25, z_max=5, offset=-25):
    x, y = get_x_and_y(-1.9, 1.9, -1.1, 1.1)
    z = -4 * ((4 - 2.1 * (x ** 2) + ((x ** 4) / 3)) * (x ** 2) + x * y + (4 * (y ** 2) - 4) * (y ** 2))
    return x, y, z, 'Six_HUmp Camel Back', z_min, z_max, offset


# 6   --2D---
def Shubert(z_min=-300, z_max=200, offset=-300):
    x, y = get_x_and_y(-10, 10, -10, 10)
    z1 = (1 * np.cos((1 + 1) * x + 1)) + (2 * np.cos((2 + 1) * x + 2)) + (3 * np.cos((3 + 1) * x + 3)) + (
            4 * np.cos((4 + 1) * x + 4)) + (5 * np.cos((5 + 1) * x + 5))
    z2 = (1 * np.cos((1 + 1) * y + 1)) + (2 * np.cos((2 + 1) * y + 2)) + (3 * np.cos((3 + 1) * y + 3)) + (
            4 * np.cos((4 + 1) * y + 4)) + (5 * np.cos((5 + 1) * y + 5))
    z = -(z1 * z2)
    return x, y, z, 'Shubert', z_min, z_max, offset


# 7 ---2D---
def Vincent(z_min=-1, z_max=1, offset=-1):
    x, y = get_x_and_y(0.25, 10, 0.25, 10)

    z1 = np.sin(10 * np.log(x))
    z2 = np.sin(10 * np.log(y))
    z = (z1 + z2) / 2
    return x, y, z, 'Vincent', z_min, z_max, offset


# 8 ---存在点问题----
def Modified_rastrigin_all_global_optima(z_min=-40, z_max=10, offset=-40):
    x, y = get_x_and_y(0, 1, 0, 1)
    z1 = 10 + 9 * np.cos(2 * np.pi * 3 * x)
    z2 = 10 + 9 * np.cos(2 * np.pi * 4 * y)
    z = -(z1 + z2)
    return x, y, z, 'Modified Rastrigin All Global Optima', z_min, z_max, offset


# Sphere Function
def Sphere(z_min = 0,z_max = 30,offset = 0):
    x,y = get_x_and_y( -3,3,-3,3)
    z = x ** 2 + y ** 2
    return x,y,z, "Sphere function", z_min, z_max, offset

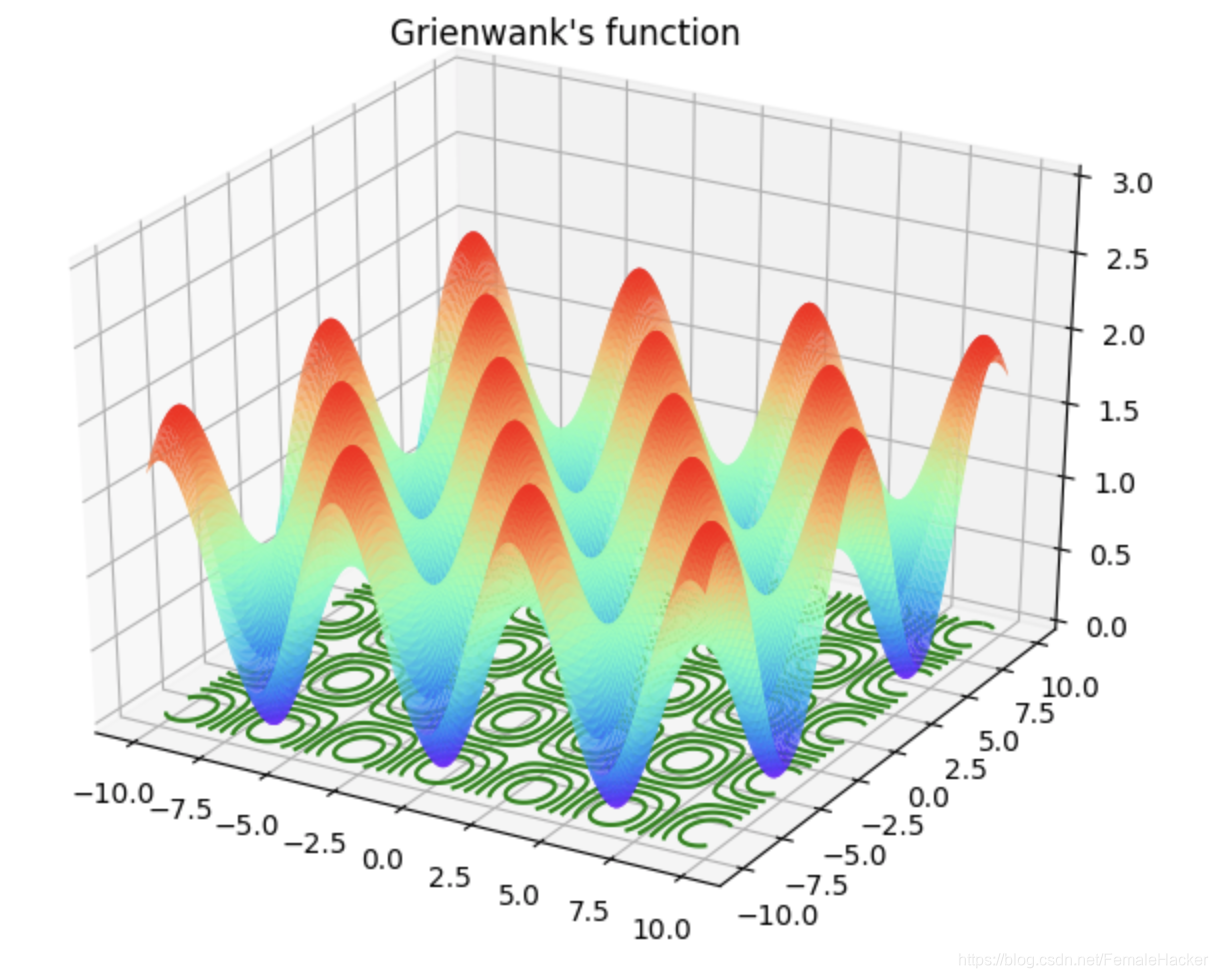
# Grienwank's Function
def Grienwank(z_min = 0,z_max = 3,offset = 0):
    x, y = get_x_and_y(-10, 10, -10, 10)
    z = (x ** 2) /4000 + (y ** 2) / 4000 - np.cos(x / np.sqrt(1)) * np.cos(y / np.sqrt(2))+1
    return x,y,z, "Grienwank's function", z_min, z_max, offset

# restrigin function
def Rastrigin(z_min=0, z_max=100, offset=0):
    x, y = get_x_and_y(-5.52, 5.12, -5.12, 5.12)
    z = 2 * 10 + x ** 2 - 10 * np.cos(2 * np.pi * x) + y ** 2 - 10 * np.cos(2 * np.pi * y)
    return x,y,z, "Rastrigin function", z_min, z_max, offset

# Weierstrass Function
def Weierstrass(z_min=-5,z_max=5,offset=-5):
    x, y = get_x_and_y(-2, 2, -2, 2)
    a = 0.5
    b = 3
    kmax = 20
    z1,z2,z3 = 0,0,0
    for k1 in range(1,kmax+1):
        z_1 = (a ** k1) * np.cos(2 * np.pi * (b ** k1) * (x + 0.5))
        z_2 = (a ** k1) * np.cos(2 * np.pi * (b ** k1) * (y + 0.5))
        z1 += z_1
        z2 += z_2
    for k2 in range(1,kmax+1):
        z_3 = (a ** k2) * np.cos(2 * np.pi * (b ** k1) * 0.5)
        z3 += z_3
    z = z1 + z2 -z3
    return x,y,z, "Weierstrass Function", z_min, z_max, offset

# Expanded Griewank's plus Rosenbrock's function (EF8F2)
def EF8F2(z_min = -100,z_max = 3000,offset = -100):
    x, y = get_x_and_y(-2, 2, -2, 2)
    f2 = 100 * ((x ** 2) - y) ** 2 + (x -1) ** 2
    z = 1 + (f2 ** 2) /4000 -np.cos(f2)
    return x,y,z, "F8F2", z_min, z_max, offset


# Five_uneven_peak_Trap
# x, y, title, x_min, x_max, y_min, y_max = Five_uneven_peak_Trap()

# Equal_maxima
# x, y, title, x_min, x_max, y_min, y_max = Equal_maxima()

# Uneven_decreasing_maxima
# x, y, title, x_min, x_max, y_min, y_max = Uneven_decreasing_maxima()

# draw_pic(x, y, title, x_min, x_max, y_min, y_max)

# -------------------------------------------------------
# Himmelblau
# x, y,z, title,z_min,z_max,offset = Himmelblau()

# Six_hump_camel_back
# x, y,z, title,z_min,z_max,offset = Six_hump_camel_back()

# Shubert
# x, y, z, title, z_min, z_max, offset = Shubert()

# Vincent
# x, y,z, title,z_min,z_max,offset = Vincent()

# Modified_rastrigin_all_global_optima
# x, y,z, title,z_min,z_max,offset = Modified_rastrigin_all_global_optima()

# Sphere Function
# x, y,z, title,z_min,z_max,offset = Sphere()

# Grienwank's Function
# x, y,z, title,z_min,z_max,offset = Grienwank()

# Rastrigin Function
# x, y,z, title,z_min,z_max,offset = Rastrigin()

# Weierstrass Function
# x, y,z, title,z_min,z_max,offset = Weierstrass()

# EF8F2
x,y,z,title, z_min, z_max, offset = EF8F2()


draw_pic_3D(x, y, z, title, z_min, z_max, offset)

效果图

转载请注明出处，多谢☺️

加油