前缀和与差分

前缀和是一种极其优秀的线性结构，也是一种十分重要的思想，能极大的降低区间查询时间复杂度。（注：前缀和数组的下标起始值为1）

那么，先来了解一下这两个概念的含义。

前缀和：前缀和指的是某序列的前n项和

差分：前缀和的逆运算

这两种运算相辅相成，合理运用可以将复杂问题简单化。

前缀和分为一维前缀和和二维前缀和，那么下面我们就分别来看一下这两种题型。

前缀和

一维前缀和

什么是一维前缀和呢，先从一个问题来引入。

问题描述：假设有一串长度为 𝑛 的序列 {𝑎1,𝑎2,𝑎3......𝑎𝑛}，给出 𝑚 次询问，每次询问给出 𝐿,𝑅 两个数，求区间 [𝐿,𝑅] 的和。

那么显而易见，最无脑的方法就是暴力求解遍历区间，时间复杂度为O(m*n)，还有TLE的风险。

这时就可以采用前缀和的方法将时间复杂度降低到O(m+n)

前缀和数组的第 𝑖 项就是一个序列前面 𝑖 个数的总和，弄清楚这个就已经完成一半了，具体的代码为

void init()
{
    sum[0] = 0;
    for(int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + a[i];
}

对于已经求出的前缀和，区间 [𝐿,𝑅] 的和即为 𝑟𝑒𝑠=𝑠𝑢𝑚[𝑅]−𝑠𝑢𝑚[𝐿−1]，代码为

int get(int L, int R)
{
    return sum[R] - sum[L - 1];
}

二维前缀和

二维前缀就是把一维前缀中的数组改成二维数组的扩展应用。

问题描述：假设有一个 𝑛∗𝑚 大小的矩阵 𝐴，再给出 𝑞 次询问，每次询问给出 𝑥1, 𝑦1, 𝑥2, 𝑦2 四个数，要求输出以 (𝑥1,𝑦1) 为左上角坐标和以 (𝑥2,𝑦2) 为右下角坐标的子矩阵的所有元素和。

如果对于每次询问都进行暴力查询，那么时间复杂度极大，一定会 TLE，此时可以利用二维前缀和来求解。

那么，如何将前缀和思想运用到二维数组中呢，以下图为例子。

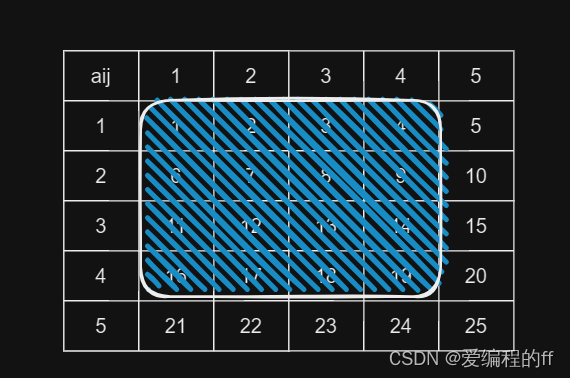
以上图a[4][4]=19为例，a[4][4]的前缀和是以蓝色斜线框起来的子矩阵元素之和，即以 (4，423) 为右下角、(1,1) 为左上角的矩阵中的元素和。

从递推的角度来，𝑠𝑢𝑚[4][4]=𝑠𝑢𝑚[4][3]+𝑠𝑢𝑚[3][4]−𝑠𝑢𝑚[3][3]+𝑎[4][4]，

那么我们由此类推，𝑠𝑢𝑚[𝑖][𝑗]=𝑠𝑢𝑚[𝑖][𝑗−1]+𝑠𝑢𝑚[𝑖−1][𝑗]−𝑠𝑢𝑚[𝑖−1][𝑗−1]+𝑎[𝑖][𝑗]

int init() 
{
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j];
}

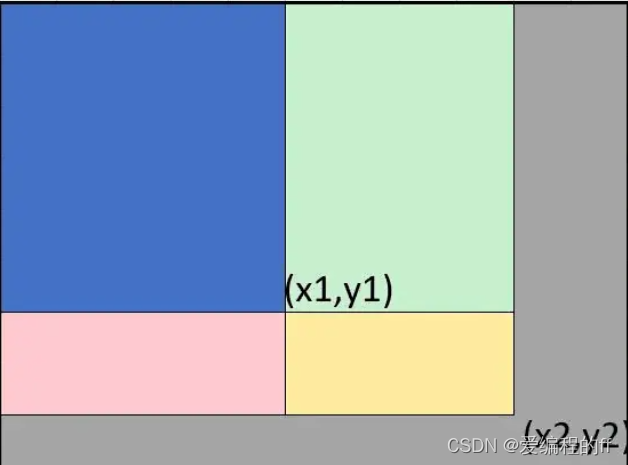
那么，每次要查询的答案就是下图中的黄色部分，当给出 𝑥1, 𝑦1, 𝑥2, 𝑦2 时，要查询的值即为 𝑟𝑒𝑠=𝑠𝑢𝑚[𝑥2][𝑦2]−𝑠𝑢𝑚[𝑥1−1][𝑦2]−𝑠𝑢𝑚[𝑥2][𝑦1−1]+𝑠𝑢𝑚[𝑥1−1][𝑦1−1]

int get(int x1, int y1, int x2, int y2) 
{
    return sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1];
}

差分

一维差分

定义：假设有原数组 𝑎[ ]={𝑎1,𝑎2,𝑎3,...𝑎𝑛}，现构造出一个数组 𝑏[ ]={𝑏1,𝑏2,𝑏3,...𝑏𝑛}，使得 𝑎𝑖=𝑏1+𝑏2+...𝑏𝑖，那么 𝑏[ ] 就称为 𝑎[ ] 的差分，𝑎[ ] 就称为 𝑏[ ] 的前缀和。可以发现，差分与前缀和是逆运算。

假如现在要将原数列 𝑎[ ] 区间 [𝐿,𝑅] 上的每个数都加上 𝑥，那么通过上述定义可以知道：

第一个受影响的差分数组中的元素为首元素𝑏[𝐿]，所以令 𝑏[𝐿]+=𝑥，那么后面数列元素在计算过程中都会加上 𝑥。最后一个受影响的差分数组中的元素为尾元素𝑏[𝑅]，所以令𝑏[𝑅+1]−=𝑥，可以保证不会影响到 𝑅 之后数列元素的计算。

这样一来，就不必对区间内每一个数进行处理，只需处理两个端点即可。

void add(int L, int R, int x)
{
    b[L] += x;
    b[R + 1] -= x;
}

那么接下来做一道题来巩固一下：

797.差分（原题链接）

输入一个长度为 n的整数序列。

接下来输入 m个操作，每个操作包含三个整数 l,r,c表示将序列中 [l,r]之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c表示一个操作。

输出格式

共一行，包含 n𝑛个整数，表示最终序列。

数据范围

1≤n,m≤100000
1≤l≤r≤n
−1000≤c≤1000
−1000≤整数序列中元素的值≤1000

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];      //构建差分数组
    }
    int l, r, c;
    while (m--)
    {
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;     //将序列中[l, r]之间的每个数都加上c
        b[r + 1] -= c;
    }
    for (int i = 1; i <= n; i++)
    {
        a[i] = b[i] + a[i - 1];    //前缀和运算
        printf("%d ", a[i]);
    }
    return 0;
}

二维差分

定义：假设有原数组 𝑎[ ][ ]，现构造出一个数组 𝑏[ ][ ]，使得 𝑎[𝑖][𝑗] 等于 𝑏[𝑖][𝑗] 格子左上部分所有元素的和，那么 𝑏[ ][ ] 就称为 𝑎[ ][ ] 的二维差分。

类比于一维差分，二维差分同样可以快速地实现如下两个操作：

1.将原数组 𝑎[ ][ ] 的以 (𝑥1,𝑦1) 为左上角、(𝑥2,𝑦2) 为右下角的矩形区域里的每个数都加上 𝑐。

// 给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c
void add(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

2.查询单点，差分数组 𝑏[𝑖][𝑗] 的前缀和就是原数组 𝑎[𝑖][𝑗] 的值。

// 求以(i,j)为右下角、(1,1)为左上角的矩阵中的元素和
void get()
{
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + b[i][j];
}