GeoGebra中级篇046—角度工具(Angle Tool)

注意：关注微信公众号“第五智能”，免费查阅全系列文章。

GeoGebra中的“角度”工具便是用于创建和测量角度的有效工具。它不仅支持通过三个点、线段、直线或向量来计算角度，还可以用于多边形的内角测量。该工具能够自动计算角度的大小，并且提供灵活的设置选项，如限制角度的大小范围等，帮助用户更直观地理解和掌握角度的性质和计算方法。

通过这个工具，用户能够在几何作图和物理仿真等多种应用场景中，清晰地展示和分析角度之间的关系，促进对角度概念的深刻理解与应用。

---

一、关于Geogebra的角度工具

1. 什么是角度工具

角度工具非常常用！非常常用！非常常用! 重要的事情说三遍。

GeoGebra中的“角度”工具，主要用于创建和测量角度。这里我们先看一下角度工具在哪里：

2. 角度工具的功能和特点

这个表格简洁地列出了“角度”工具的主要功能和特点：

功能	描述
通过三个点创建角度	选择三个点，创建以第二个点为顶点、由其余两个点确定的角度。
通过线段创建角度	选择两个线段，GeoGebra计算这两条线段之间的夹角。
通过直线创建角度	选择两条直线，GeoGebra计算它们之间的夹角。
通过向量创建角度	选择两个向量，GeoGebra计算这两个向量之间的角度。
多边形的内角	选择一个多边形，GeoGebra会计算并显示该多边形的所有内角。
角度方向	创建的角度具有逆时针方向，选择的顺序决定了角度的方向。
角度大小限制	可以在属性对话框中通过下拉列表限制角度的大小范围（如0°到180°）。
命令支持	使用命令Angle[point1, point2, point3]来创建角度，适用于三点、线段、直线、向量等多种情况。

3. 角度工具的常见用途

这个表格列出了过两点画半圆工具在几何构造、教学、证明等方面的常见应用，希望对你有帮助。

用途	描述
几何作图与证明	使用角度工具构造各种几何图形，如等腰三角形、正多边形等，帮助学生理解图形中的角度关系。同时，可以用来验证几何定理或进行角度相关的证明。
分析平面几何问题	在解决平面几何问题时，通过测量角度，分析不同线段、直线、向量之间的夹角，帮助解答问题，如计算三角形的内角和、判断两条直线是否平行等。
物理仿真中的角度分析	在物理学中，例如研究力的分解、运动轨迹、旋转等问题时，角度工具可用于精确测量力的方向或物体的运动轨迹与基准线之间的夹角，辅助物理实验与模拟。
角度变化规律的研究	通过动态调整点的位置，研究角度的变化规律，例如观察角度随三角形顶点移动的变化，或探索角度与图形变形的关系。
解决三角学问题	通过角度工具，快速计算和验证三角学中的各种角度关系，如内外角公式、正弦定理、余弦定理等，帮助解题。
建筑与工程设计	在建筑设计或工程领域，使用角度工具测量和设计结构的角度，以确保设计图纸和施工过程中的角度准确性，特别是对于复杂结构的角度测量和验证。
机器人与机械臂路径规划	在机器人路径规划和机械臂控制中，角度工具帮助计算各个关节之间的夹角，确保路径的精确性，避免碰撞，优化运动轨迹。
天文学中的角度测量	在天文学中，角度工具可用于测量天体之间的视角距离，帮助研究天体的运动、相对位置等。

二、角度工具的使用

1. 基本使用

（1）通过三个点

选择三个已有的点，注意着三个点中，第二个点一定是角度的位置。

（2）通过两个线段

选择两个线段，GeoGebra将计算这两条线段之间的角度。（这个没难度，就是选择两条线段）

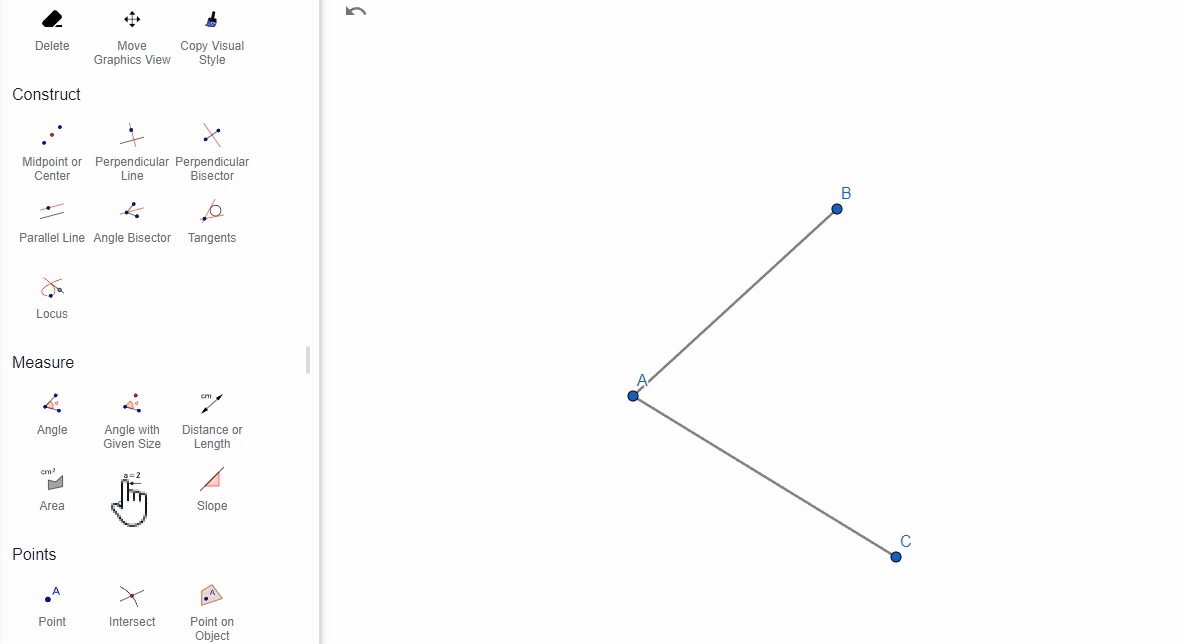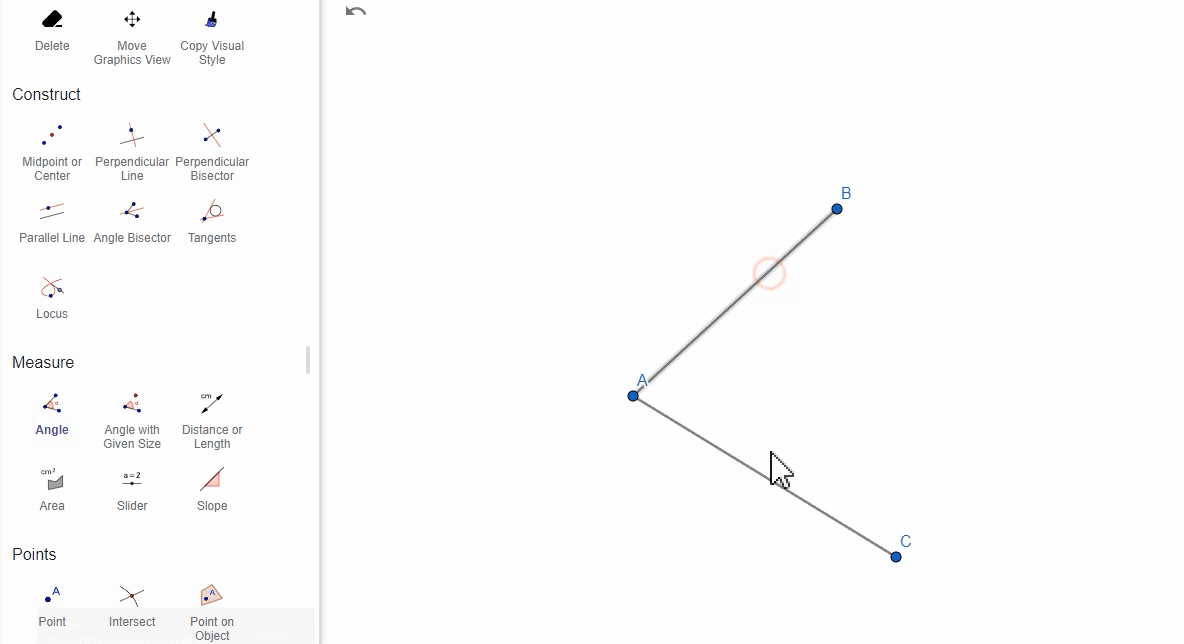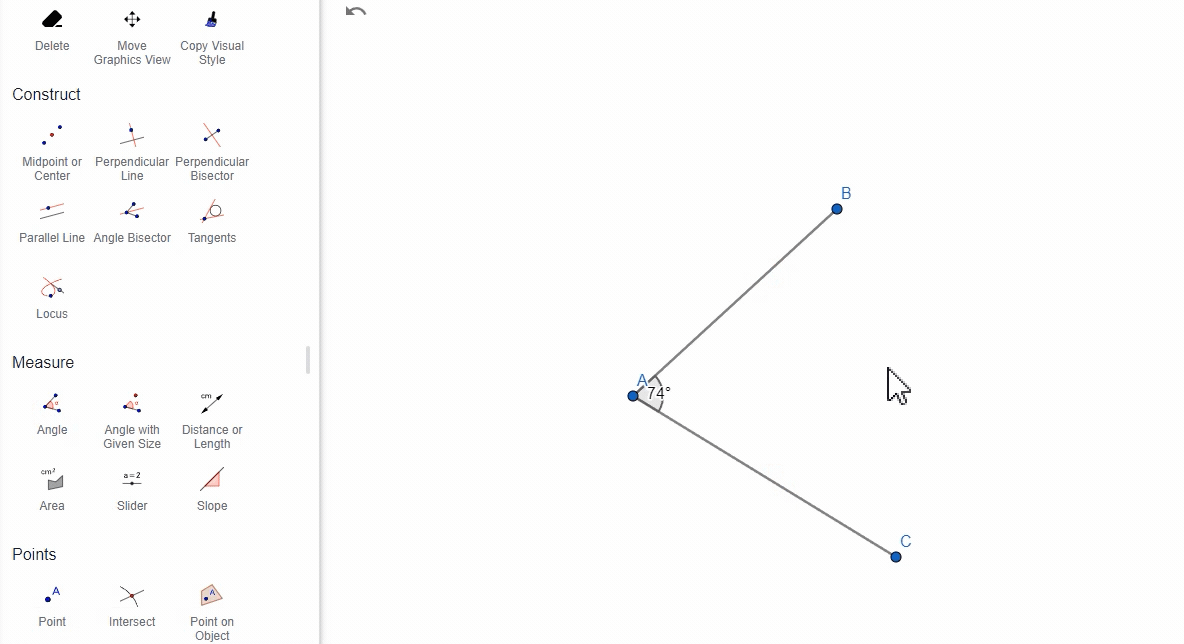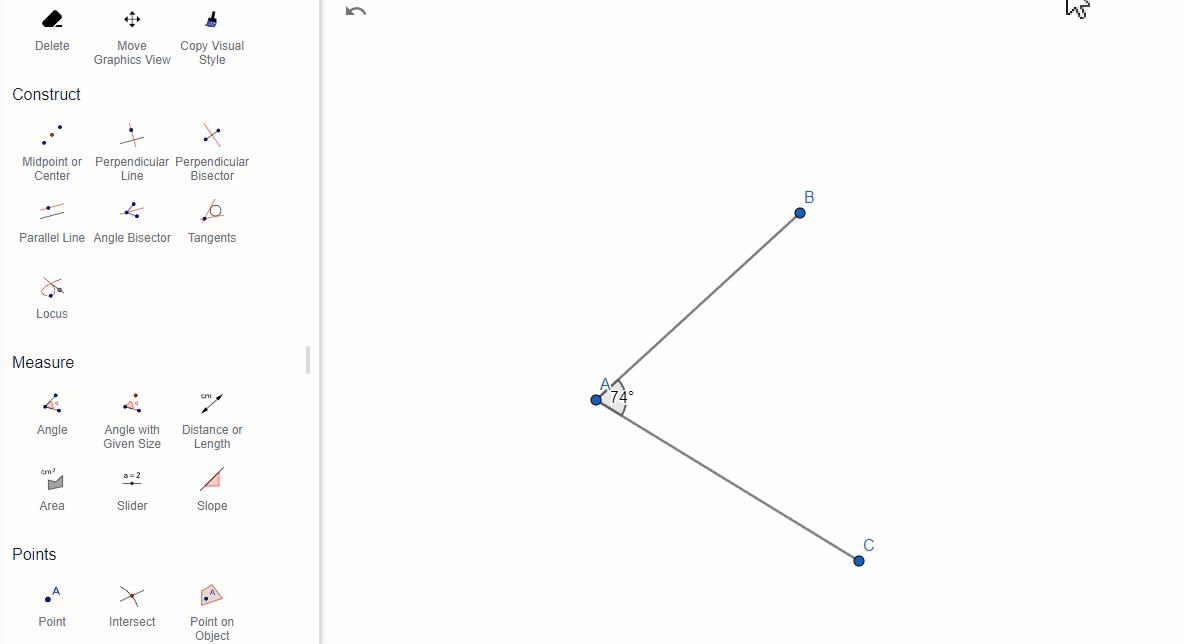
（3）通过两条直线

如果有两条直线，那么选择两条直线的时候，GeoGebra会计算它们的夹角。

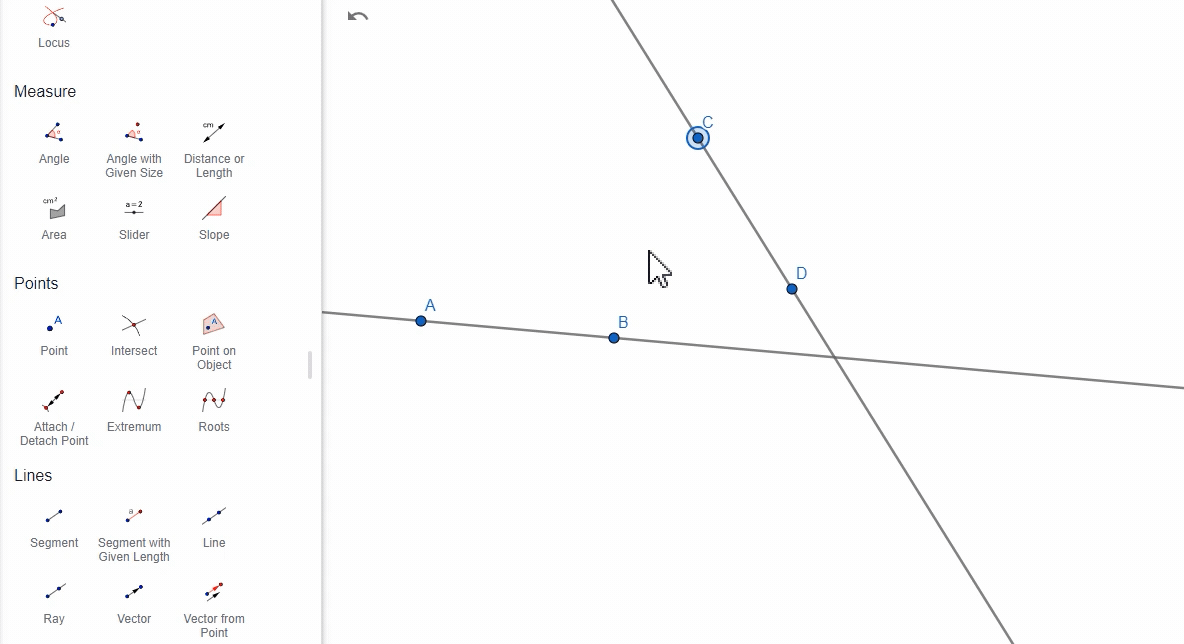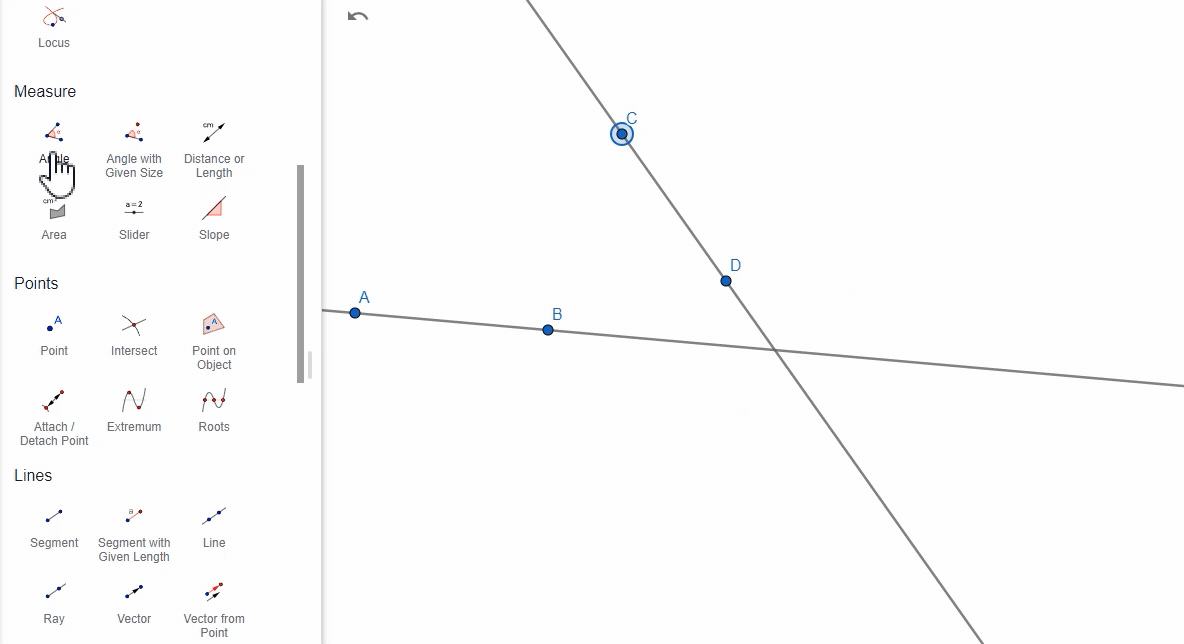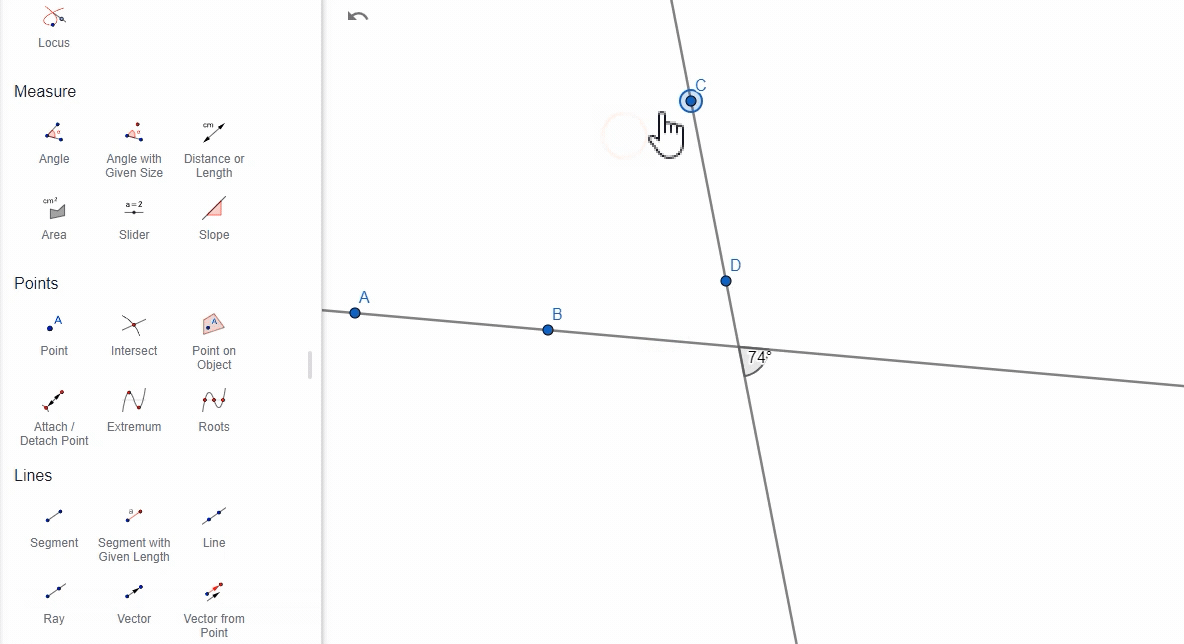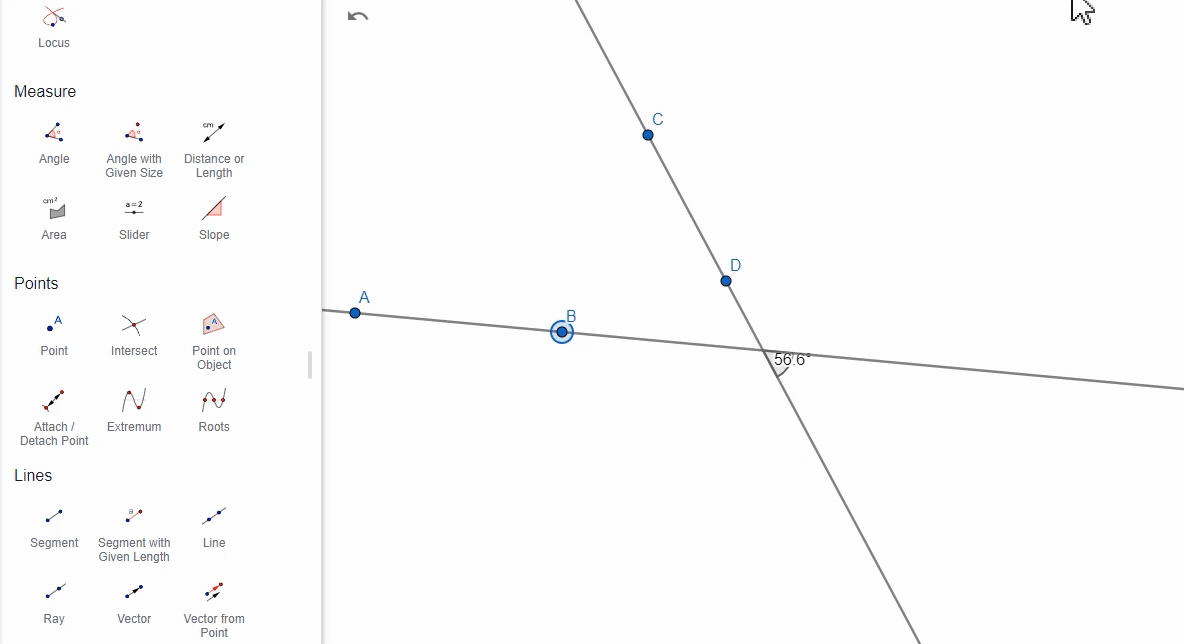
注意：

1. GeoGebra在计算两条直线之间的夹角时，默认计算的是锐角（即小于 90° 的角）。如果两条直线的夹角大于 90°，GeoGebra仍然会返回小于 90° 的锐角，而不是钝角。
2. 如果你需要计算更大的角度（即钝角），需要在指令栏手动计算。例如，如果计算得到的夹角是 30°，你想要得到钝角，可以用 180° - 30° 来得到钝角 150°，但这种方式比较少见，因为实战中都是用角度来控制直线，而非先产生直线再测算角度。

（4）通过两个向量

选择两个向量，GeoGebra计算这两个向量之间的角度。

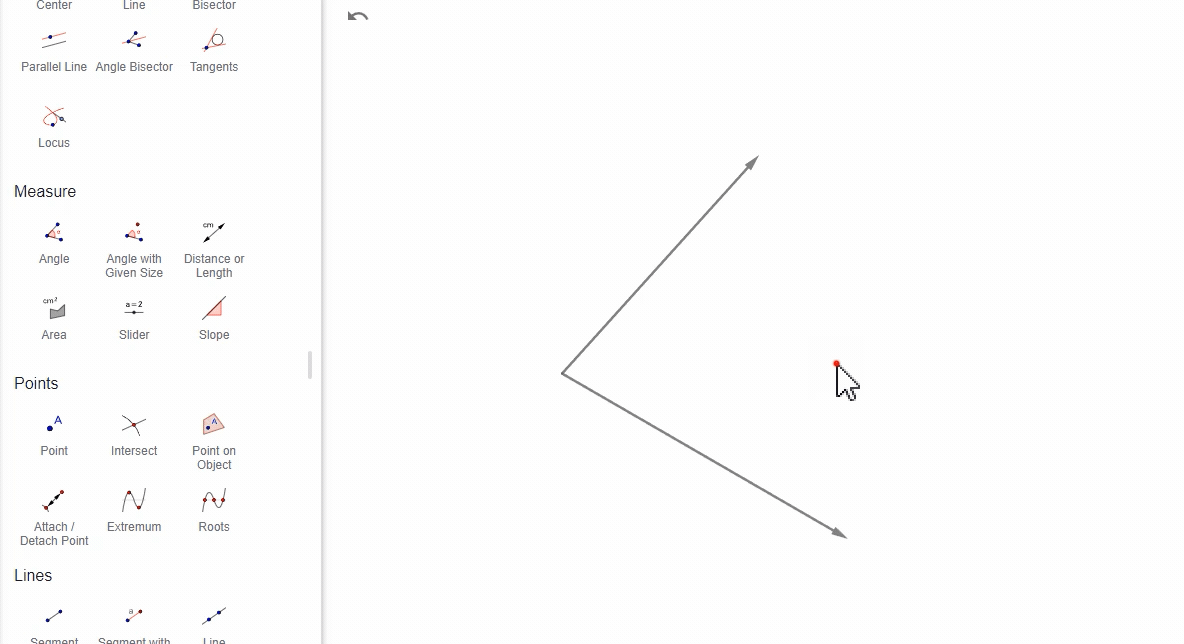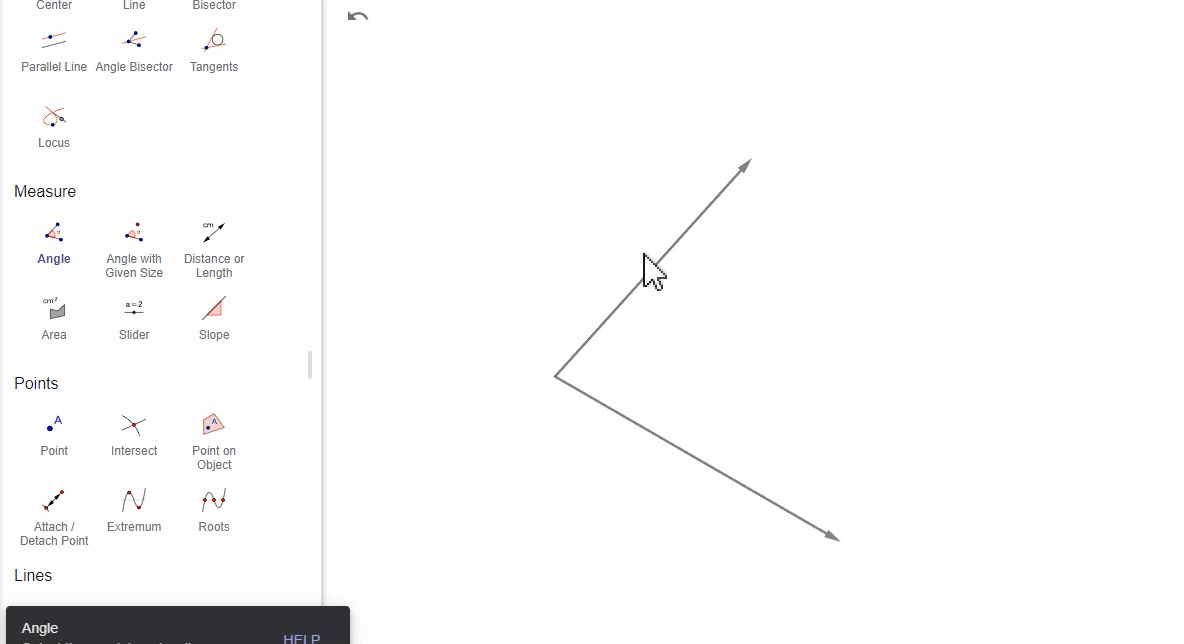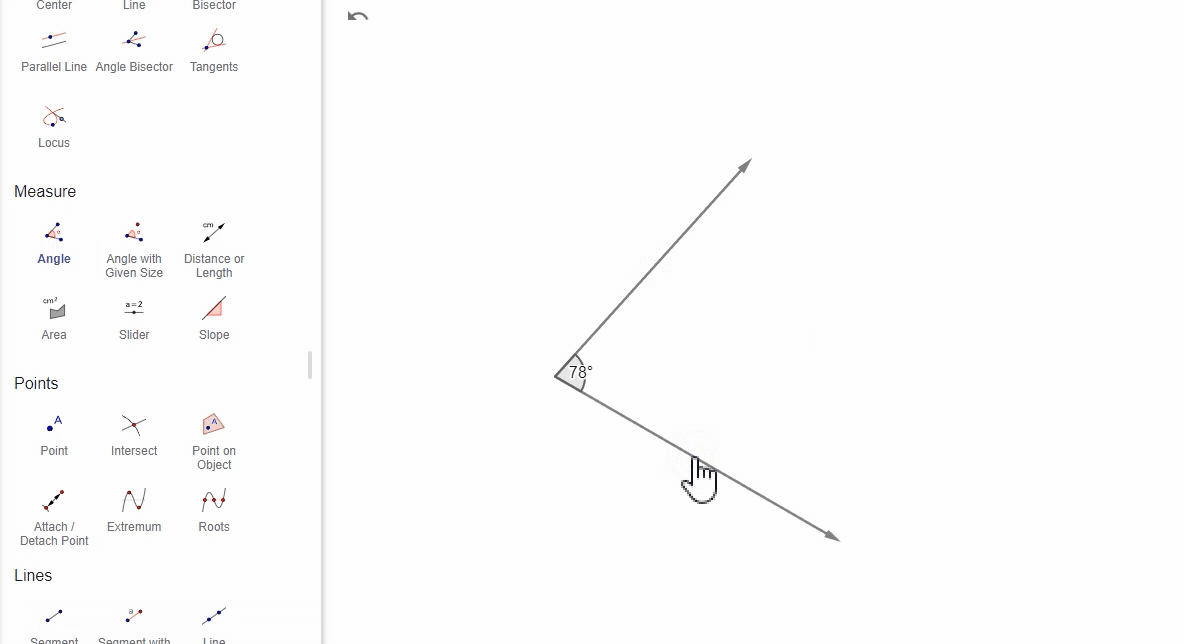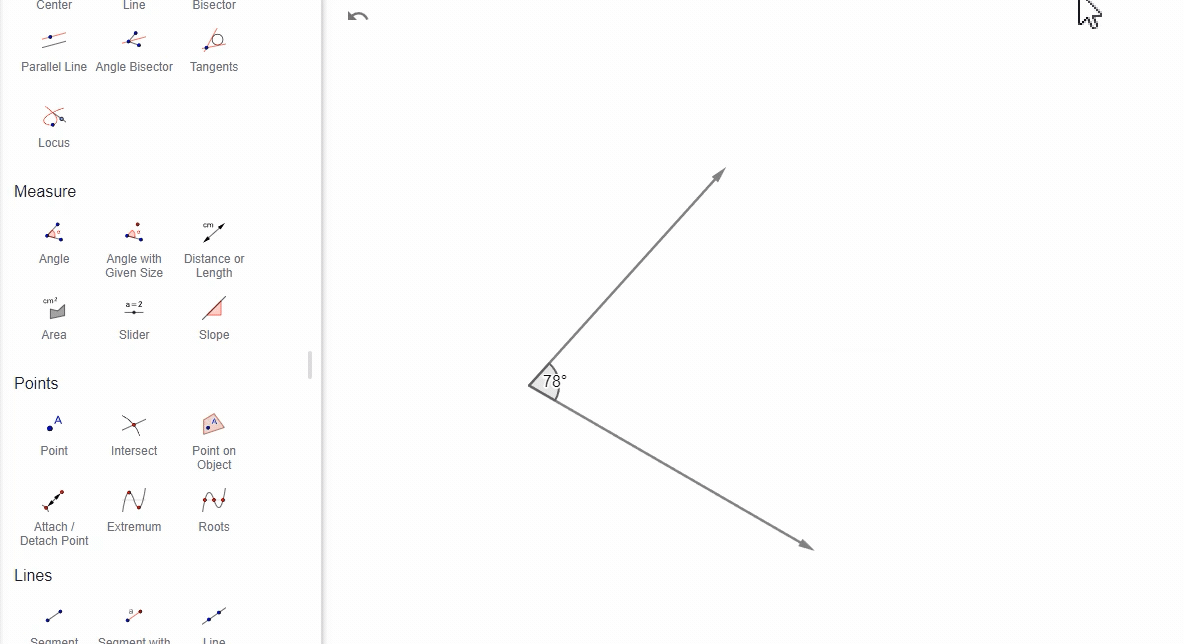
（5）通过多边形

选择一个多边形，GeoGebra将计算并显示多边形的所有内角。

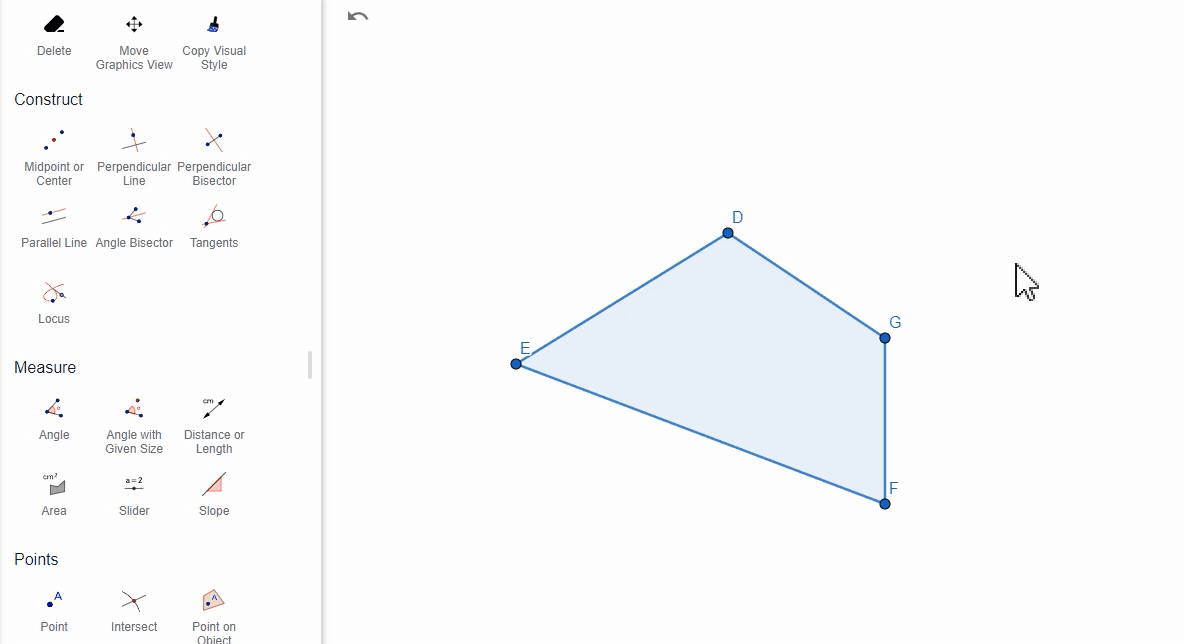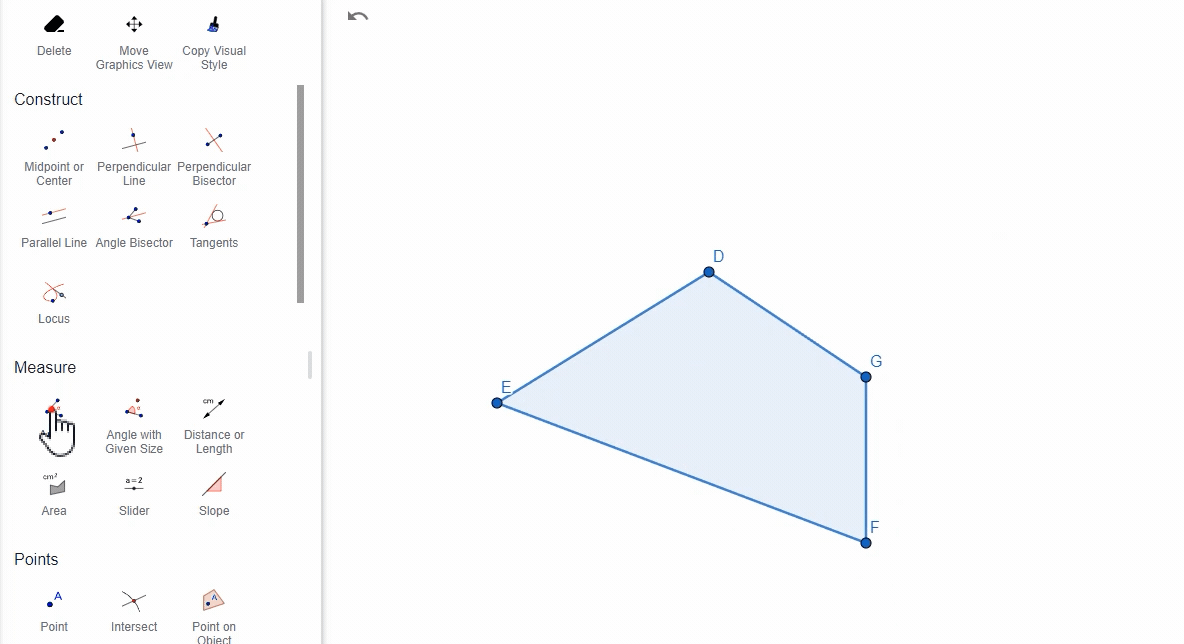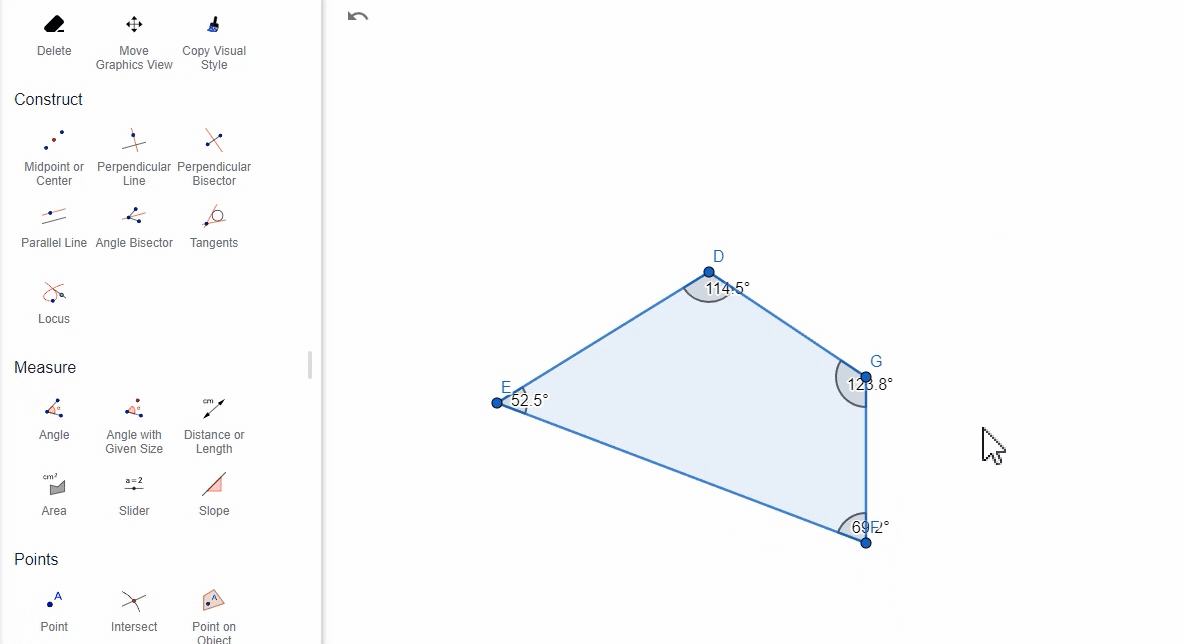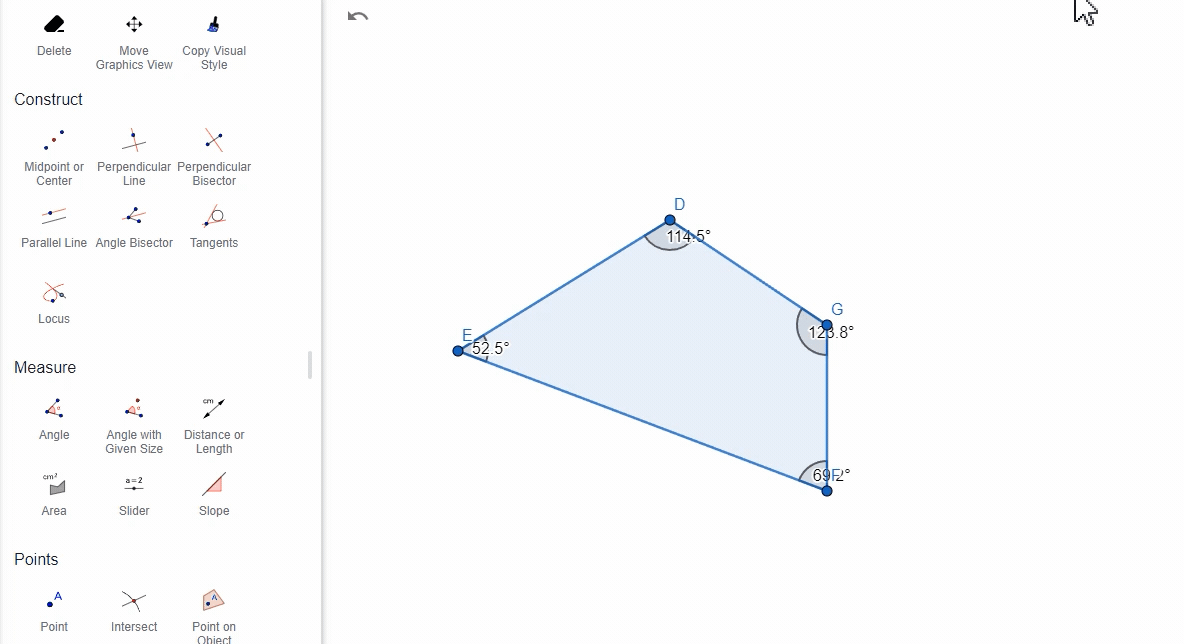
2. 注意事项

这个表格总结了实战中在使用角度工具时需要注意的一些事项，帮助你避免常见的错误或误解

角度工具使用注意事项

注意事项	描述
选择顺序影响角度方向	由于GeoGebra默认按逆时针方向计算角度，因此选择的顺序非常重要。确保正确选择点、线段、直线或向量，以获得正确的角度方向。
计算的是锐角	当计算两条直线或两条向量的夹角时，GeoGebra只会返回小于 90° 的锐角。如果需要获取钝角，需要手动计算（180° - 锐角）。
多边形角度计算	使用角度工具计算多边形的内角时，GeoGebra会自动计算并显示所有内角，但需要注意角度的度量单位是否设置为度或弧度。
角度范围限制	在属性对话框中，可以通过下拉列表限制角度的范围（例如，限制角度在 0° 到 180° 之间）。务必确认角度大小设置符合需求。
不支持自动计算外角	角度工具计算的是两条直线或两条向量的夹角，不会自动计算外角。如果需要计算外角，需使用补角公式（180° - 内角）。
直线与向量之间的夹角	计算两条直线或两向量之间的夹角时，GeoGebra会默认计算它们的最小夹角，即锐角。如果需要更大角度，需要手动调整。
动态变化	角度工具支持动态变化，当改变点的位置时，角度会随之变化，能够帮助理解角度随几何形状变化的规律。
精度问题	当点之间的距离非常小或非常大时，角度计算可能会出现精度误差。尽量保持合适的缩放级别和图形清晰度，以获得准确结果。

三、综合案例：多边形的内角和

记得之前有位客户找我们定制多边形的内角和，结果我们是通过两线的方式逐个计算内角的，但其实有更好的方式，那就是我们今天研究的角度工具：

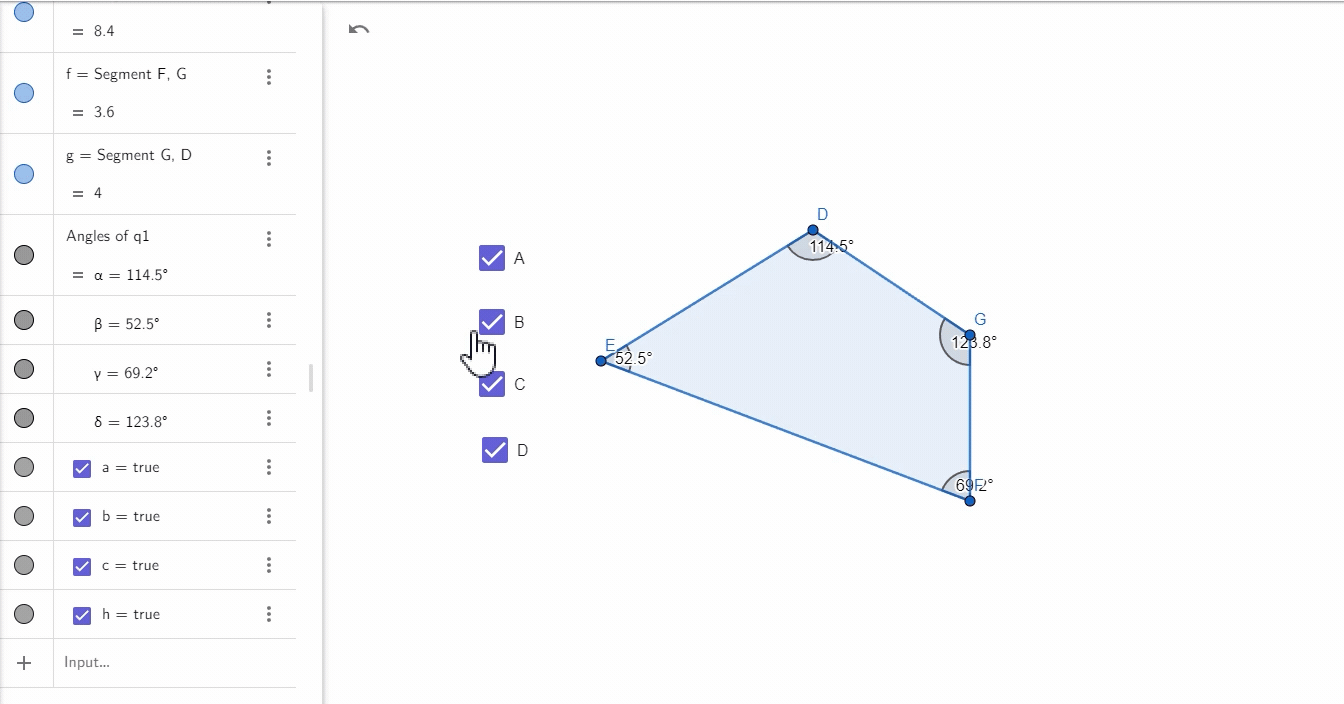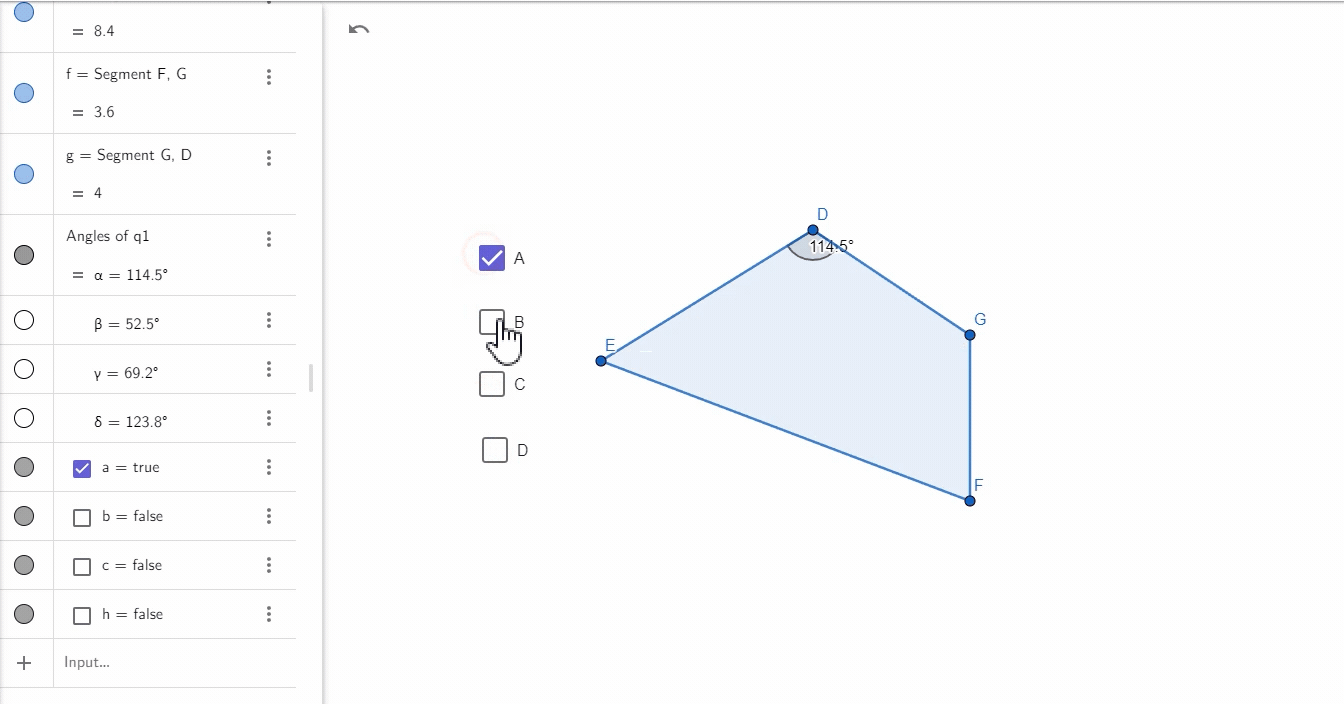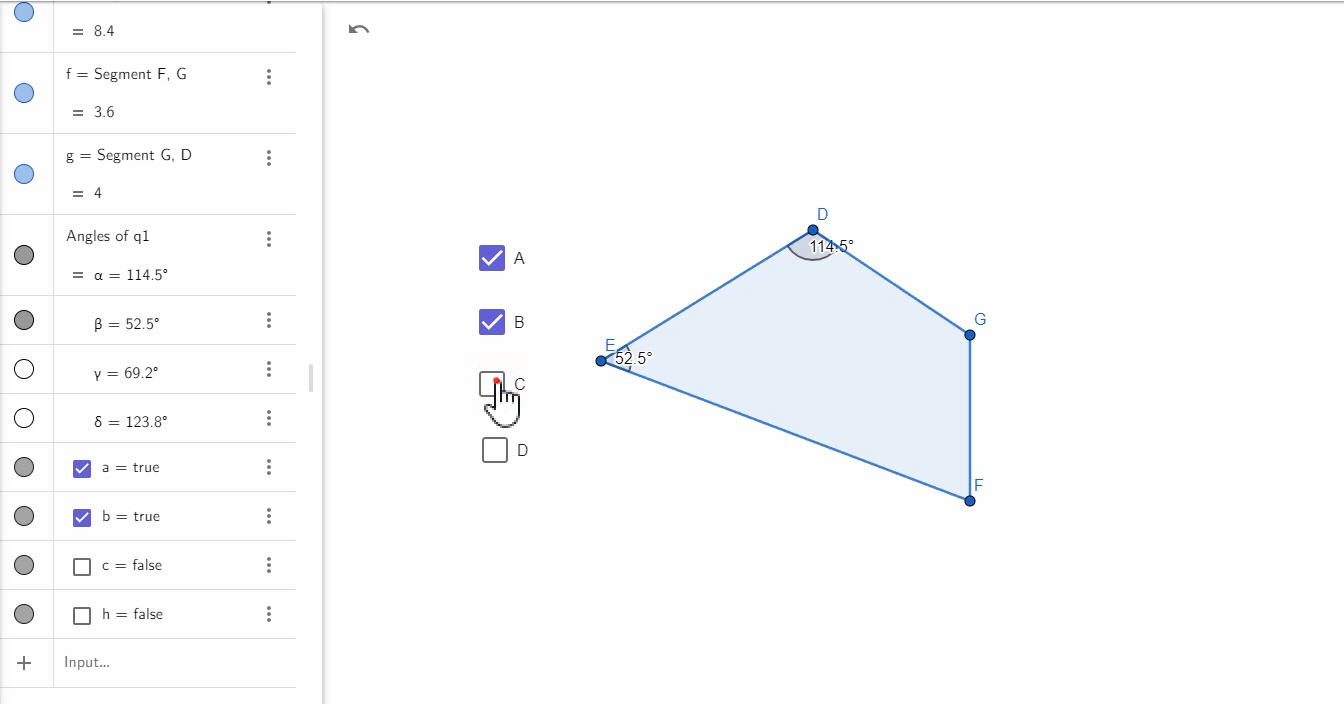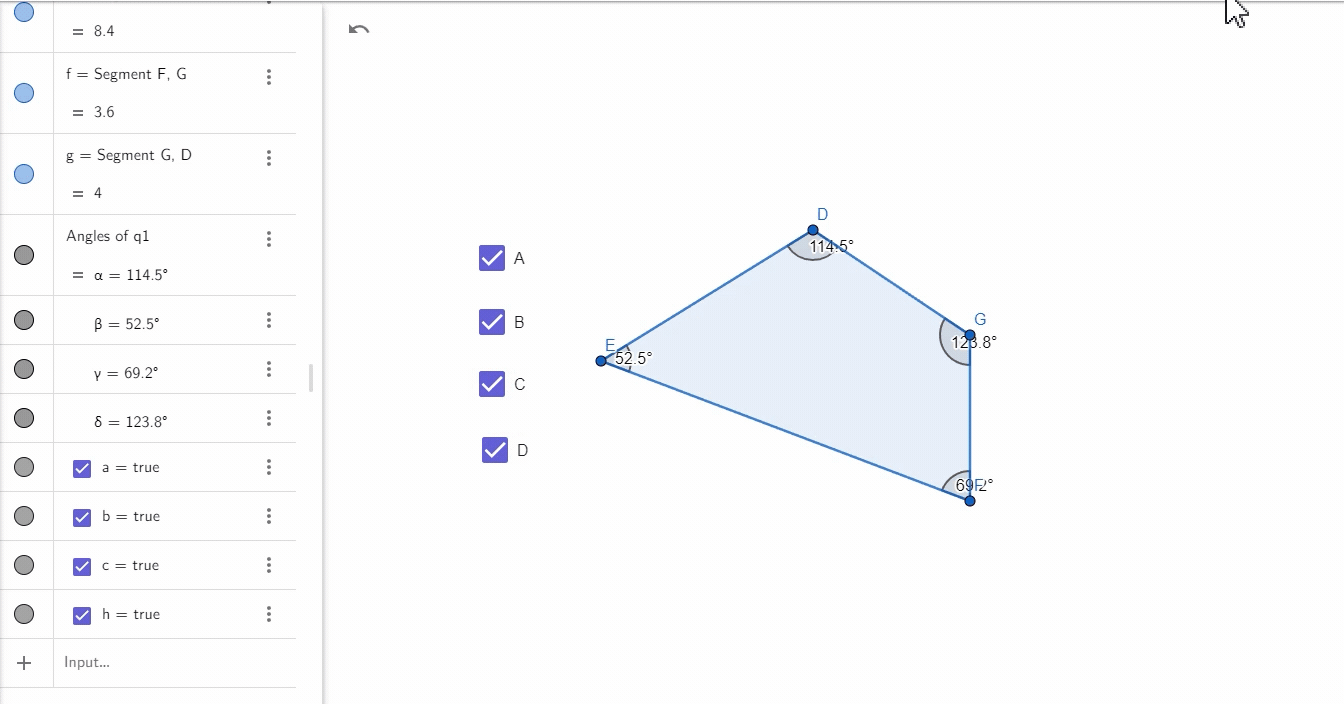
一键快速找出多边形的内角和，属实方便。下边放上本次案例的指令集：

D=(8.72513,3.44783)
E=(4.1879,0.64417)
F=(12.08524,-2.35211)
G=(12.08524,1.20062)
q1=Polygon(D,E,F,G)
d=Segment(D,E,q1)
e=Segment(E,F,q1)
f=Segment(F,G,q1)
g=Segment(G,D,q1)
InteriorAngles(q1)

四、文章最后

好啦，本篇就到这里。

还没有关注的宝子们注意咯，点击下方链接进行关注，您的鼓励是我们持续创作的动力。我们每天都会更新Geogebra教程，希望对您有帮助。若有其他需要可以在公众号内点击第五店铺进行客服咨询。全天24小时在线，祝你工作顺利。