CodeForces 670D Triangles

D. Triangles

Little Petya likes to draw. He drew N red and M blue points on the plane in such a way that no three points lie on the same line. Now he wonders what is the number of distinct triangles with vertices in red points which do not contain any blue point inside.
Input

The first line contains two non-negative integer numbers N and M (0 ≤ N ≤ 500, 0 ≤ M ≤ 500) — the number of red and blue points respectively. The following N lines contain two integer numbers each — coordinates of red points. The following M lines contain two integer numbers each — coordinates of blue points. All coordinates do not exceed 109 by absolute value.
Output

Output one integer — the number of distinct triangles with vertices in red points which do not contain any blue point inside.
Examples
Input

4 1
0 0
10 0
10 10
5 4
2 1

Output

2

Input

5 5
5 10
6 1
8 6
-6 -7
7 -1
5 -1
10 -4
-10 -8
-10 5
-2 -8

Output

7

题意：给出二维坐标系内一些红色的点和蓝色的点，问红色的点能组成多少个不包含蓝色点的三角形

题解：

大意是这样的，首先枚举一个红点A，对其他点按照该点进行极角排序，
枚举第二个红点B确定一条边，枚举第三个点C，若为蓝点更新最小的$∠ACB$,若为红点则判断组成的三角形是否合法，看图就明白了：

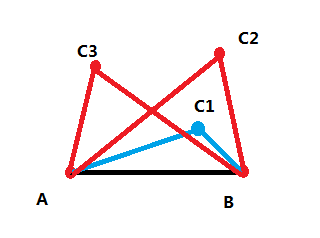
此时如果要计算合法的三角形，那么一定有$∠C_2AB>∠C_1AB且∠C_2BA＞∠C_1BA$，由于此时已经进行了极角排序，所以$∠CAB$是严格递增了，那么只需要在遇到蓝色点时不断更新$∠CBA$就能在$O（n）$的复杂度内判断所有的合法三角形。

HINT
1.判断角的大小时利用叉积性质判断，如果直接用$cos$去进行精度误差太大，long double也无法精确表示
2.蓝点和红点放在一起极角排序判断
3.double比longlong要快300ms

#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<map>
#include<cstdlib>
#include<cmath>
#include<vector>
//#pragma comment(linker, "/STACK:1024000000,1024000000");

using namespace std;

#define INF 0x3f3f3f3f

struct Point
{
    double x,y;
    int kind;
    int id;
    Point() {}
    Point(double _x,double _y)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
//叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
//点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
//绕原点旋转角度B（弧度值），后x,y的变化
    void transXY(double B)
    {
        double tx = x,ty = y;
        x = tx*cos(B) - ty*sin(B);
        y = tx*sin(B) + ty*cos(B);
    }
} p[1505],q[1505];

const double eps = 1e-8;
const double PI = acos(-1.0);

bool cmp(Point a,Point b)
{
    if(a.y==b.y) return a.x<b.x;
    return a.y<b.y;
}

int sgn(double x)
{
    if(x==0)return 0;
    if(x < 0)return -1;
    else return 1;
}

double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}

int nowp;
bool _cmp(Point p1,Point p2)
{
    double temp = (p1-p[nowp])^(p2-p[nowp]);
    if(sgn(temp) > 0)return true;
    else if(sgn(temp) == 0 && sgn(dist(p1,p[nowp]) - dist(p2,p[nowp])) <= 0)
        return true;
    else return false;
}

int ans=0;
int n,m;
void solve(int k,int len)
{
    for(int i=k+1; i<len; i++)
    {
        if(q[i].kind==2) continue;
        int la=k;
        for(int j=i+1; j<len; j++)
        {
            double temp=(q[j]-q[i])^(q[la]-q[i]);
            if(q[j].kind==1)
            {
                if(temp<0||la==k)
                {
                    ans++;
                }
            }
            else
            {
                if(temp<0||la==k)
                {
                    la=j;
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int len=n+m;
    for(int i=0; i<n+m; i++)
    {
        scanf("%lf%lf",&p[i].x,&p[i].y);
        p[i].id=i;
        if(i<n) p[i].kind=1;
        else p[i].kind=2;
    }
    sort(p,p+len,cmp);
    int len1=0;
    for(int i=0; i<len; i++)
    {
        if(p[i].kind==2) continue;
        nowp=i;
        for(int j=nowp;j<len;j++) q[j]=p[j];
        sort(q+nowp,q+len,_cmp);
        solve(nowp,len);
    }
    printf("%d\n",ans);
    return 0;
}