堆的相关问题思考和二级结论求堆排序时间复杂度

  前言：今天学习一下堆方面的知识。一开始对堆的刻板印象是二叉树，底层以为是用链表构成的，学了堆方面的知识发现原来是用数组实现的。简单来说就是堆的逻辑结构是完全二叉树，而物理结构却是存放在数组中连续的。

一、堆

1 堆的结构

  堆的结构体定义是由数组构成，那么必不可少的是堆的动态开辟空间和堆存的有效数据和容量。

typedef struct Heap
{
	HPDataType* a;
	int size; //有效数据个数
	int capacity; //容量
}HP; 

2 堆的初始化和扩容

  既然存了有效数据个数，必然面临空间满而带来的扩容问题
初始化：先给四个整形的空间不够再扩容。

void HeapInit(HP* php)
{
	assert(php);
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
	php->capacity = 4; 
	php->size = 0;
}

3 堆的判满，大小，堆顶数据和堆的销毁

  比较简单直接上代码

HPDataType HeapTop(HP* php) //堆顶元素
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}
bool HeapEmpty(HP* php) //判空
{
	assert(php);
	return php->size == 0;
}
int HeapSize(HP* php) //大小
{
	assert(php);
	return php->size;
}
void HeapDestroy(HP* php) //销毁
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

二、堆的插入

  在堆中插入，说明前面插入的元素要构成堆。插入后仍要保持堆的性质，这里我们构建大堆。大堆即双亲比左右孩子都要大。

1 插入元素

  插入元素前记得检查是否需要扩容

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	CheakCapacity(php);
	php->a[php->size] = x;
	AdjustUp(php->a, php->size);
	php->size++;
}

2 向上调整构建堆

（1） 动图理解

  向上调整，若插入的元素比它的双亲大，则需要交换他们的位置，再迭代向上调整，直到孩子比双亲小。

（2） 代码实现

void AdjustUp(HPDataType* a, int child)
{
	assert(a);
	int parent = (child - 1) / 2;
	while (child >= 0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
				//开始往上迭代
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
				//前提是前面的数据构成大堆
			break;
		}
	}
}

三、堆的删除

  删除堆顶元素前先检查堆是否为空再向下调整,这里我们要思考为什么删除堆顶的元素而不对堆尾的元素，堆尾的元素方便删除，但是实用性不高，删出堆顶的元素可以解决生活中的TopK问题。

1 为什么不直接删除堆顶数据?

  删除堆顶元素后，当左孩子较大的时候，可能会出现数组空洞，就不是完全二叉树了。



  在这里我们学习一种比较好的方法，先让堆顶元素和堆尾元素交换一下，然后堆大小size–就访问不到最后的元素了，再向下调整还原堆

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

2 向下调整还原堆

（1） 动图理解

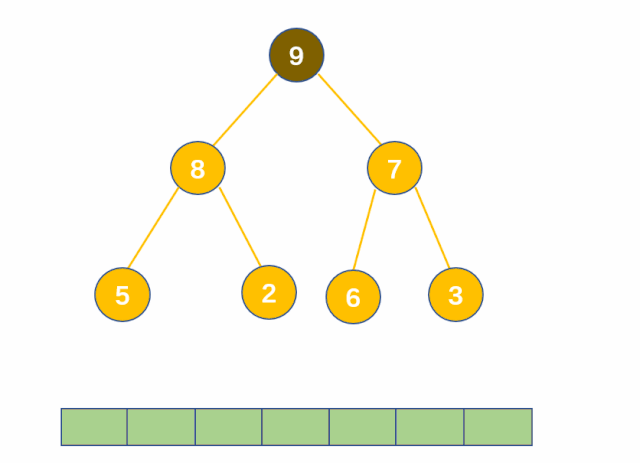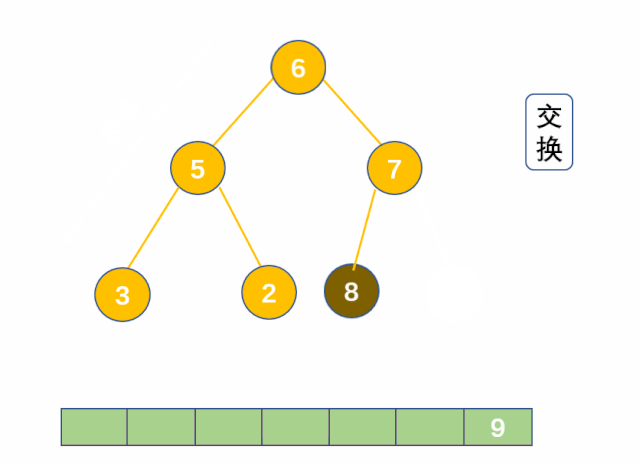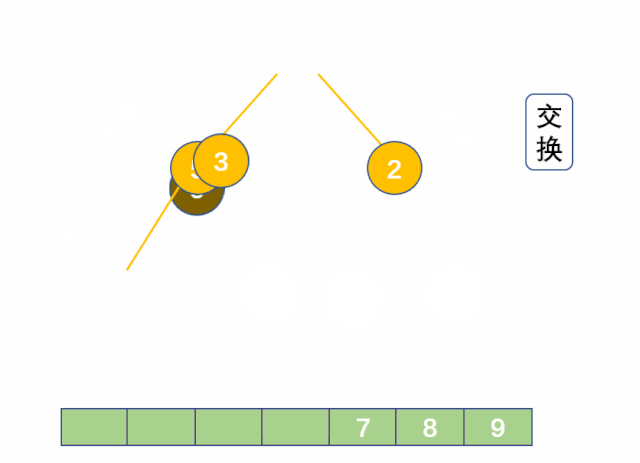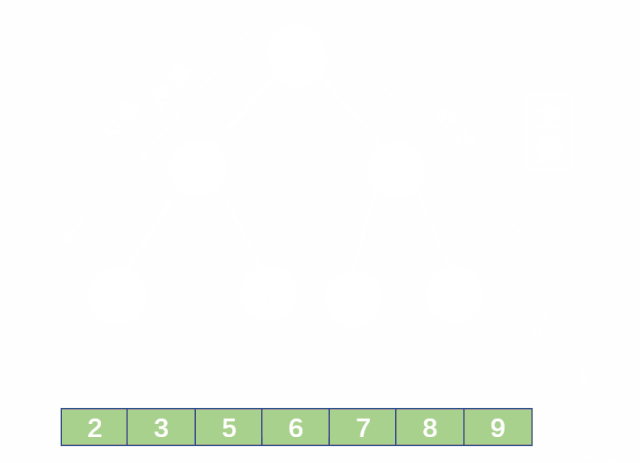
（2） 代码实现

  这里还原大堆，先要找到左右孩子中较大的那一个，再往下迭代，同时注意细节，应先默认左孩子大，因为右孩子可能不存在，直接设有孩子大可能存在溢出的情况。

void AdjustDown(HPDataType* a, int size, int parent)
{
		//默认左孩子大，因为右孩子可能不存在就越界了
	int child = parent * 2 + 1;

	while (child < size)
	{
			//找到左右孩子中大的那一个
		if (child + 1 < size && a[child] < a[child + 1])
			child++;	//注意防止child+1>size

		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			//除了调整元素外其他元素构成堆
			break;
		}
	}
}

四、堆排序

1 思考为什么排升序建大堆，降序建小堆？

  如果要通过建小堆完成让数组升序排列的话，因为小堆堆顶元素是最小值，而堆顶这个位置也是排序之后最小值的位置就是说堆顶元素不用在移动了，那么我们的堆要从后面一位重新建立，在建立一个小堆，找出最小值，在往后面一位找出最小值直到整个数组成升序排列，乍一看好像没有问题，但是和建大堆不同的是建小堆每次都要从下一位重新建堆才能选出最值，这个操作的复杂度为$O(nlogn)$,要比建大堆每次只用将堆顶元素向下调整的时间复杂度为$O(logn)$满很多，所以虽然可以升序建小堆但是因为相对没有建大堆速度快所以我们选择建大堆。
  对应的降序建小堆也是同理。

2 堆的构建

（1）向上调整法$O(nlogn)$

  向上调整法模仿堆的插入过程时间复杂度为nlogn,这里我们假设堆有$h$层，第$k$层需要向上调整$k-1$次,则第$k$层需要调整数$(k-1)\ast 2^{k-1}$即$a_n=(n-1)\ast 2^{n-1}$

$S_n=2^0*0+2^1*1+……+2^{n-1}*(n-1)$ $2S_n=2^1*0+2^2*1+……+2^n*(n-1)$ 错位相减得： $S_n=2^n*(n-1)-(2^1+2^2+……+2^{n-1})=2^n*(n-2)+2))$ 又$N=2^n-1$所有时间复杂度为$O(nlogn)$

void HeapSort(int* a, int size)
{
	for (int i = 1; i < size; i++)
	{
		AdjustUp(a, i);
	}
	int end = size - 1;
	while(end>0)
	{
		Swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		--end;
	}
}

（2）向上调整法复杂度证明二级结论$S_n=(An+B)\ast q^n-B)$

  在上面我们已经知道了第n层$a_n=(n-1)\ast 2^{n-1}$,而高中有个二级结论，这种数列它得前n项和必为$S_n=(An+B)\ast q^n-B)$,在次我们可以求出$S_1=a_1=0,S_2=1\ast 2^1=2$
$S_1=(A+B)\ast 2^1-B=2A+B=0$
$S_2=(2A+B)\ast 2^2-B=8A+3B=2$
联立两式得$A=1,B=-2,因此S_n=(n-2)\ast 2^n+2$
$在此时间复杂度为O(nlogn)显然$

（3）向下调整法$O(N)$

  向下调整法是从堆的倒数的一个非叶子结点开始调整，时间复杂度肯定要小于$O(nlogn)$ 。这里我们设堆有$h$层

$S_n=2^0\ast (h-1)+2^1\ast (h-2)+\dots \dots +2^{h-2}\ast 1$
$2S_n=2^1\ast (h-1)+2^2\ast (h-2)+\dots \dots +2^{h-1}\ast 1$
错位相减得：
$S_n=2^1+2^2+2^{(h-2)}+2^{h-1}-1+h=2^h-1+1-h=2^h-h$
$又2^h-1=N则时间复杂度为O(N)$

void HeapSort(int* a, int size)
{
		//从倒数第一个叶子结点开始向下调整堆
	for (int i = (size - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, size, i);
	}
		//每次把堆首尾交换，大的数字在最后面，在调回大堆
	int end = size - 1;
	while(end>0)
	{
		Swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		--end;
	}
}

3 模仿堆的删除进行排序

  在这里我们模仿堆的删除，把堆首尾元素换一下，一次便排好了一个数，在进行堆调整即可,代码已经附上堆调整上面。

总结

  堆的内容就到此结束了，希望二级结论求堆向上调整的时间复杂度对你有所帮助，期待我们在下一篇博客见面！