Flip Game
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 37055 | Accepted: 16125 |
Description
Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
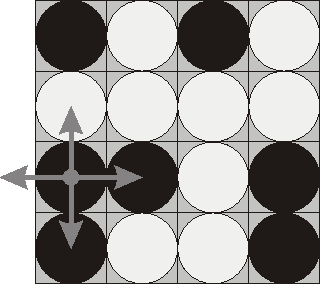 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
- Choose any one of the 16 pieces.
- Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.
Output
Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).
Sample Input
bwwb bbwb bwwb bwww
Sample Output
4
思路:
和前面那些问题差不多吧,只是它最后结果要求全黑或者全白,所以算了两次
poj1753
/*
同样的基于二维矩阵的开关问题,只是题目要求最终结果要
全亮或者全黑,于是算两次即可
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
typedef long double ld;
using namespace std;
const int maxn = 40;
int equ,var;
int a[maxn][maxn];
int b[maxn][maxn];
int x[maxn];
int free_x[maxn];
int free_num;
int Gauss()
{
int max_r,col,k;
free_num = 0;
for(k = 0,col = 0; k < equ && col < var; k++,col++)
{
max_r = k;
for(int i = k+1; i < equ; i++)
{
if(abs(a[i][col]) > abs(a[max_r][col]))
max_r = i;
}
if(a[max_r][col] == 0)
{
k --;
free_x[free_num++] = col;
continue;
}
if(max_r != k)
{
for(int j = col; j < var+1; j++)
swap(a[k][j],a[max_r][j]);
}
for(int i = k + 1; i < equ; i++)
{
if(a[i][col] != 0)
{
for(int j = col; j < var+1; j++)
a[i][j] ^= a[k][j];
}
}
}
for(int i = k; i < equ; i++)
if(a[i][col] != 0)
return -1;
if(k < var) return var-k;
for(int i = var-1; i >= 0; i--)
{
x[i] = a[i][var];
for(int j = i +1; j < var; j++)
x[i] ^= (a[i][j] && x[j]);
}
return 0;
}
int n;
void ini()
{
memset(a,0,sizeof(a));
memset(x,0,sizeof(x));
equ = n*n;
var = n*n;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
int tt = i*n+ j;
a[tt][tt] =1;
b[tt][tt] = 1;
if(i > 0) a[(i-1)*n+j][tt] = 1;
if(i < n-1) a[(i+1)*n+j][tt] = 1;
if(j > 0) a[tt-1][tt] = 1;
if(j < n-1) a[tt+1][tt] =1;
}
}
}
int solve()
{
int t = Gauss();
if(t == -1)
{
return t;
}
else if(t == 0)
{
int ans = 0;
for(int i = 0; i < n*n; i++)
ans += x[i];
return ans;
}
else
{
int ans = 0x3f3f3f3f;
int tot = (1 << t);
for(int i = 0; i < tot; i++)
{
int cnt = 0;
for(int j = 0; j < t; j++)
{
if(i & (1 << j))
{
cnt ++;
x[free_x[j]]= 1;
}
else x[free_x[j]]= 0;
}
for(int j = var-t-1; j >= 0; j--)
{
int dex;
for(dex = j; dex < var; dex++)
if(a[j][dex])
break;
x[dex] = a[j][var];
for(int l = dex +1; l <var ; l++)
{
if(a[j][l])
x[dex] ^= x[l];
}
cnt += x[dex];
}
ans = min(ans,cnt);
}
return ans;
}
}
char str[30][30];
int main()
{
int T;
char color;
scanf("%d",&T);
while(scanf("%s",str[0]) !=EOF)
{
n = 4;
ini();
for(int j = 0; j < n; j++)
{
if(str[0][j] == 'b')
{
a[j][n*n] = 0;
}
else
{
a[j][n*n] = 1;
}
}
for(int i = 1; i < n; i++)
{
scanf("%s",str[i]);
for(int j = 0; j < n; j++)
{
if(str[i][j] == 'b')
{
a[i*n+j][n*n] = 0;
}
else
{
a[i*n+j][n*n] = 1;
}
}
}
int ans1 = solve();
//cout <<ans1 <<endl;
ini();
for(int i = 0;i < n;i++)
{
for(int j = 0;j < n;j++)
{
if(str[i][j] == 'b')
{
a[i*n+j][n*n] = 1;
}
else
{
a[i*n+j][n*n] = 0;
}
}
}
int ans2 = solve();
//cout << ans2<<endl;
if(ans1 == -1 && ans2 == -1)
printf("Impossible\n");
else if(ans1 == -1)
printf("%d\n",ans2);
else if(ans2 == -1)
printf("%d\n",ans1);
else
printf("%d\n",min(ans1,ans2));
}
return 0;
}
























 4437
4437

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








