一、整数线性规划基础
二、常用求解方法:
1. 割平面法、
2. 分支定界法
-

-
对于不满足约束或者小于下届的分支还需要进行剪枝操作。
3. 隐枚举法
三、算例及实现代码
3.1 整数线性规划常见的第三方库和软件(截图来自B站)
(1) 软件:Excel, Lingo和matlab
(2) 第三方库
补充:
- pulp: Lp models
- OpenOpt: Lp models, non-LP models

3.2 这里我们先学习使用pulp求解器来求解一个问题
3.2.1 基于anaconda的pulp安装
3.2.2 求解一个算例,来自B站
- 算例描述
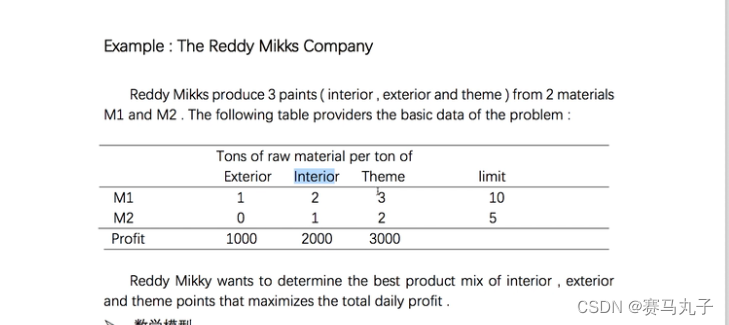
某公司生产三种油漆(interior, exterior, theme),油漆的原材料来源为M1和M2, 现在M1和M2分别只剩10吨和5吨了,三种油漆每吨的利润分别是:1k,2k和3k,三种油漆每生产一吨需要的原材料重量如下表所示,要求如何分配原材料的配置,使得利润最大化,注意这里并不是整数线性规划问题,原材料的分配可以为小数。
- 数学模型
(1) 变量
| 变量名 | 含义 |
|---|---|
| x1 | interior产量 |
| x2 | exterior产量 |
| x3 | theme产量 |
(2) 目标函数
| c o n s t _ f u n c t i o n = 1000 ∗ x 1 + 2000 ∗ x 2 + 3000 ∗ x 3 const\_function=1000*x1+2000*x2+3000*x3 const_function=1000∗x1+2000∗x2+3000∗x3 | (1) |
(3) 约束
| x 1 + x 2 ∗ 2 + x 3 ∗ 3 < = 10 x1+x2*2+x3*3<=10 x1+x2∗2+x3∗3<=10 | (2) |
| x 1 ∗ 0 + x 2 + x 3 ∗ 2 < = 5 x1*0+x2+x3*2<=5 x1∗0+x2+x3∗2<=5 | (3) |
| x 1 , x 2 , x 3 > = 0 x1,x2,x3>=0 x1,x2,x3>=0 | (4) |
- 代码实现
from pulp import *
prob=LpProblem("my_prob",LpMaximize)
x1=LpVariable("x1",0,None,LpContinuous)
x2=LpVariable("x2",0,None,LpContinuous)
x3=LpVariable("x3",0,None,LpContinuous)
prob+=1000*x1+2000*x2+3000*x3
prob+=x1+x2*2+3*x3<=10
prob+=0*x1+x2+x3*2<=5
prob.writeLP("my_prob.lp")
prob.solve()
print("status: ",LpStatus[prob.status])
for v in prob.variables():
print(v.name," = ",v.varValue,"\n")
print(value(prob.objective))
输出
status: Optimal
x1 = 2.5
x2 = 0.0
x3 = 2.5
10000.0
3.3 pulp进阶:新增函数
- 还是上一节的问题,但是变量定义方式变了
利用LpVariable.dicts(name, indexs,lowBound=None,upBound=None, cat='Continuous',indexStart=[])用来构造变量字典,可以不需要一个个创建Lp变量实例,name指定所有变量前缀,index是列表,其元素会被用来构造变量名,后面三个参数和LpVariable一样。 lpSum(vector)计算一个序列的值,使用lpSum求解比普通sum函数快。
LpVariable
from pulp import *
paints={"interior","exterior","theme"}
profit={
"interior":1e3,
"exterior":2e3,
"theme":3e3
}
M1={
"interior":1,
"exterior":2,
"theme":3
}
M2={
"interior":0,
"exterior":1,
"theme":2
}
prob=LpProblem("my_prob",LpMaximize)
var=LpVariable.dicts("paint",paints,0,None,LpContinuous)
prob+=lpSum([profit[i]*var[i] for i in paints])
prob+=lpSum([M1[i]*var[i] for i in paints])<=10
prob+=lpSum([M2[i]*var[i] for i in paints])<=5
prob.writeLP("my_prob.lp")
prob.solve()
print("status: ",LpStatus[prob.status])
for v in prob.variables():
print(v.name," = ",v.varValue,"\n")
print(value(prob.objective))
输出
status: Optimal
paint_exterior = 0.0
paint_interior = 2.5
paint_theme = 2.5
10000.0
注意这一次的输出变量名和第一次输出的变量名有所区别,这里的变量名是库自己生成的。










 本文介绍了整数线性规划的基础知识,包括割平面法、分支定界法和隐枚举法等求解方法。通过实例展示了如何使用Python的pulp库求解整数线性规划问题,详细解释了数学模型的建立和代码实现过程,并提供了两种不同的变量定义方式。最后,文章还介绍了pulp的进阶用法,如利用LpVariable.dicts和lpSum函数提高效率。
本文介绍了整数线性规划的基础知识,包括割平面法、分支定界法和隐枚举法等求解方法。通过实例展示了如何使用Python的pulp库求解整数线性规划问题,详细解释了数学模型的建立和代码实现过程,并提供了两种不同的变量定义方式。最后,文章还介绍了pulp的进阶用法,如利用LpVariable.dicts和lpSum函数提高效率。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








