个人随意总结知识——数据结构教程（第5版）【李春葆】

GJunan

已于 2023-02-14 17:01:40 修改

阅读量2.9k

点赞数 8

文章标签：数据结构

于 2023-02-09 19:37:47 首次发布

本文链接：https://blog.csdn.net/GJunan/article/details/128825531

版权

asd

第一章绪论

数据结构的概念（逻辑结构存储结构数据运算）

数据类型……

算法：五大特性：有穷性确定性可行性输入输出

算法分析：时间复杂度（时间数量级）空间复杂度（主要是临时存储空间）

第二章线性表

顺序表链表（单链表双链表循环链表）

第三章栈与队列

顺序栈链栈顺序队列链队列双端队列

中缀表达式（数学中使用的）1 + 2 * 3 ，运算符左右两边数字与运算符相计算；

中缀表达式可以与以下两种相互转化：

前缀表达式 + 1 * 2 3 ，运算符右边两位数字与运算符相计算；

后缀表达式 1 2 3 * + ，运算符左边两位数字与运算符相计算。

运用栈的思想，将运算符压入栈中，根据情况出栈。

第四章串

顺序串链串

串的模式匹配：

Brute-Force算法: t为模式串，暴力匹配目标串s串

#include <iostream>
#include <string>

using namespace std;

int BF(string s, string t);//Brute-Force算法

int main()
{
	string s = "aaaaab";
	string t = "aaab";
	cout << BF(s, t) << endl;
}

int BF(string s, string t)//Brute-Force算法
{
	int i = 0, j = 0;
	while (i < s.length() && j < t.length())
	{
		if (s[i + j] == t[j])
		{
			j++;
		}
		else
		{
			j = 0;
			i++;
		}
	}
	if (j >= t.length()) return i + 1;
	else return -1;
}

KMP算法（Knuth-Morris-Pratt算法）：

KMP算法是BF算法的改进，主要消除了主串指针的回溯。

NEXT数组怎么求？手写如图：

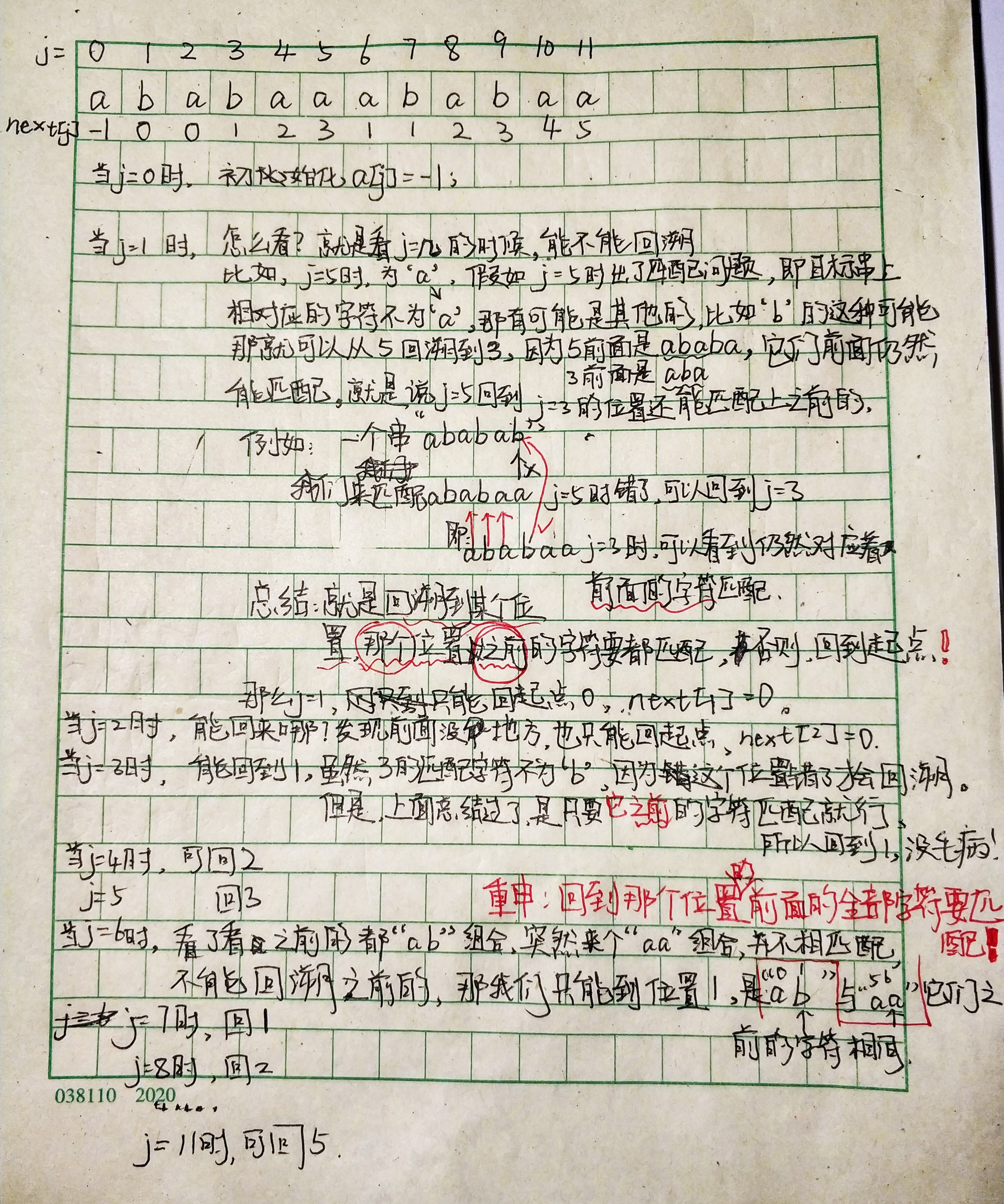
也就是说NEXT数组是模式串出错后回溯到原来具有同样信息的子串的位置上，不判断第j位是否相同，继续匹配，如若出错则继续回溯。（后面的nextval改进了next，减少了冗余判断重复回溯）

#include <iostream>
#include <string>

using namespace std;

void getnext(string t, int NEXT[]);
int KMP(string s, string t);//KMP算法

int main()
{
	string s = "aaaaab";
	string t = "aaab";
	cout << KMP(s, t) << endl;
}

void getnext(string t, int NEXT[])
{
	NEXT[0] = -1;
	int i = 0, j = -1;
	while (i < t.length() - 1)
	{
		if (j == -1 || t[i] == t[j]) NEXT[++i] = ++j;
		else j = NEXT[j];
	}
}

int KMP(string s, string t)//KMP算法
{
	const int Max_size = 20;
	int NEXT[Max_size];
	getnext(t, NEXT);
	int i = 0, j = 0;
	while (i < s.length() && j < t.length())
	{
		if (j == -1 || s[i] == t[j])
		{
			i++;
			j++;
		}
		else
		{
			j = NEXT[j];
		}
	}
	if (j >= t.length()) return i - t.length();
	else return -1;
}

我们匹配两个串是否存在相等区段，用KMP算法需要先求出NEXT回溯数组，当匹配出错时模式串t向前回溯，优化了BF算法；但是任然存在缺陷，就是没比较t串的第j位置与回溯位置是否匹配，若不匹配，则直接滑动目标串，模式串直接重新开始匹配。

求 NEXTVAL就是在原有NEXT的基础上增加第j位的判断：

void getnextval(string t, int NEXTVAL[])
{
	NEXTVAL[0] = -1;
	int i = 0, j = -1;
	while (i < t.length() - 1)
	{
		if (j == -1 || t[i] == t[j])
		{
			i++;
			j++;
			if (t[i] != t[j]) NEXTVAL[i] = j;
			else NEXTVAL[i] = NEXTVAL[j];
		}
		else
		{
			j = NEXTVAL[j];
		}
	}
}

第五章递归

递归分而治之是种思想,我们用它来解决可以转化成子问题的大的复杂问题，建立递归模型（递归体、递归出口），这里就以最经典的汉诺塔为例：

编写一个hanoi函数，传入三根塔柱的字符标识，我们的递归出口就是n=1的情况，递归体就是n>1的情况。我们在面对大规模汉诺塔问题时，只需要采用递归思想，将复杂的问题简单化，

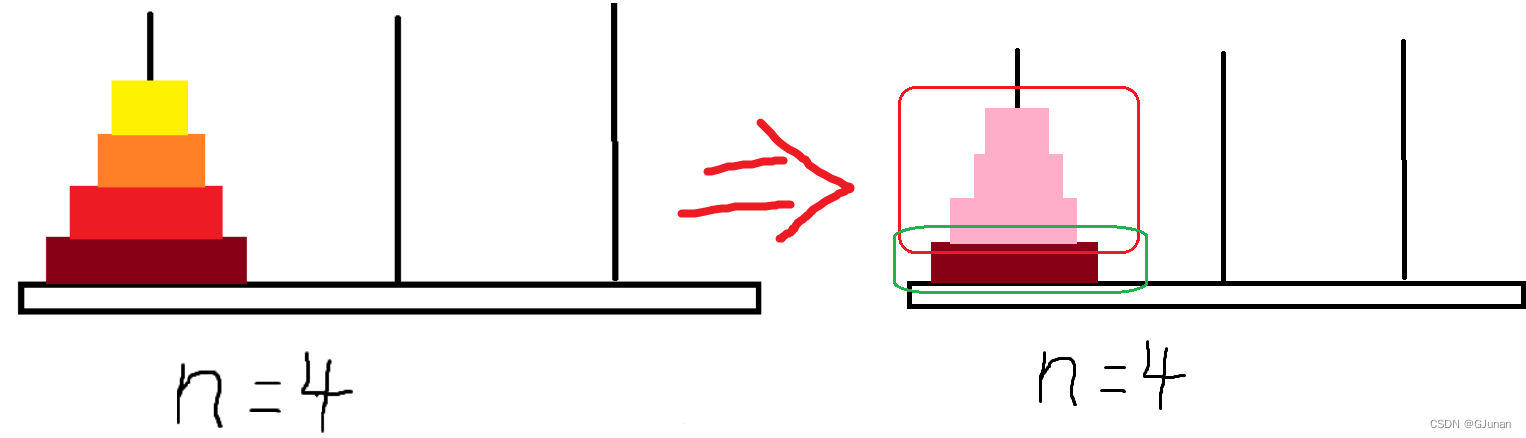
把上层的片都看作整体，这样就把问题简化成n=2的情况，此时我们只需要将大块移动到中间的柱子上，就可以让最长的塔片移动到最右边的目标柱，再将中间的大块组合片移动到最右边，这就完成了递归体的构造：①先让上面的部分移动到中间 ②将最长片移动到目标柱 ③再将中间的盘片移动到目标柱上。

我们的递归出口就是n=1时的情况，只有一个盘片，即将这一个盘片移动到目标柱。

#include <iostream>
using namespace std;

void hanoi(char A, char B, char C, int n);//汉诺塔

int main()
{
	int n;
	cin >> n;
	hanoi('A', 'B', 'C', n);
}

void hanoi(char A, char B, char C, int n)//汉诺塔
{
	if (n == 1) cout << A << " -> " << C << endl;
	if (n >= 2)
	{
		hanoi(A, C, B, n - 1);
		cout << A << " -> " << C << endl;
		hanoi(B, A, C, n - 1);
	}
}

第六章数组与广义表

介绍一些特殊的数据结构三元组、十字链表……

第七章树与二叉树

树的基本数据结构……

树的遍历：先根遍历、层次遍历、后根遍历

二叉树严格区分左右子树，可以为空。

二叉树、树与森林之间的转化。

二叉树的链式存储结构：

typedef int ElemType;

typedef struct node
{
	ElemType data;        //数据元素
	struct node* lchild;  //指向左孩子结点
	struct node* rchild;  //指向右孩子结点
}BTNode;		          //Binary Tree Node 二叉树结点

二叉树的遍历：

递归：

先序遍历：先根遍历，NLR，先访问根节点，先序遍历左子树，先序遍历右子树。

void PreOrder(BTNode* b)//先序遍历
{
	if (b != NULL)
	{
		cout << b->data << endl;
		PreOrder(b->lchild);
		PreOrder(b->rchild);
	}
}

中序遍历：LNR，中序遍历左子树，访问根节点，中序遍历右子树。

void InOrder(BTNode* b)//中序遍历
{
	if (b != NULL)
	{
		InOrder(b->lchild);
		cout << b->data << endl;
		InOrder(b->rchild);
	}
}

后序遍历：后根遍历，LRN，后序遍历右子树，后序遍历左子树，访问根节点。

void PostOrder(BTNode* b)//后序遍历
{
	if (b != NULL)
	{
		PostOrder(b->lchild);
		PostOrder(b->rchild);
		cout << b->data << endl;
	}
}

非递归：

层次遍历逐层从左到右访问左右结点。

二叉树的构造：

先序序列和中序序列或后序序列和中序序列可以唯一确定二叉树。

线索二叉树：由不同遍历方式创建线索化的二叉树，提高遍历二叉树的效率。

typedef struct node
{
	ElemType data; //数据元素
	int ltag, rtag;//线索或孩子标记
	struct node* lchild;  //指向左孩子结点或线索指针
	struct node* rchild;  //指向右孩子结点或线索指针
}TBTNode;		   //Tag Binary Tree Node 二叉树结点

哈夫曼树：带权路径长度（WPL，Weighted Path Length）最小的二叉树称为哈夫曼树或最优二叉树。方法：每次选两个最小权值组建二叉树。

并查集……

第八章图

图的基本概念

图的存储结构和基本运算算法：邻接矩阵存储方法、邻接表存储方法(出度)、逆邻接表(入度)、十字链表、临界多重表。

一般用邻接矩阵进行数据录入，使用邻接表进行应用：

//图的两种存储结构
#define INF 32767				//定义∞
#define	MAXV 100				//最大顶点个数
typedef char InfoType;

//以下定义邻接矩阵类型
typedef struct
{	int no;						//顶点编号
	InfoType info;				//顶点其他信息
} VertexType;					//顶点类型
typedef struct
{	int edges[MAXV][MAXV];		//邻接矩阵数组
	int n,e;					//顶点数，边数
	VertexType vexs[MAXV];		//存放顶点信息
} MatGraph;						//完整的图邻接矩阵类型

//以下定义邻接表类型
typedef struct ANode
{	int adjvex;					//该边的邻接点编号
	struct ANode *nextarc;		//指向下一条边的指针
	int weight;					//该边的相关信息，如权值（用整型表示）
} ArcNode;						//边结点类型
typedef struct Vnode
{	InfoType info;				//顶点其他信息
	int count;					//存放顶点入度,仅仅用于拓扑排序
	ArcNode *firstarc;			//指向第一条边
} VNode;						//邻接表头结点类型
typedef struct 
{	VNode adjlist[MAXV];		//邻接表头结点数组
	int n,e;					//图中顶点数n和边数e
} AdjGraph;						//完整的图邻接表类型

图的遍历：

深度优先遍历(Depth First Search，DFS)：

采用递归，创立一个遍历数组visited[vertex],未遍历的点赋值为0，已搜索过的点赋值为1。

每次搜索先输出该起点，并且visited值改为1，创建一个指针p指向下一个相邻结点，开始深度遍历，用一个循环确保相邻结点都被遍历，在循环中判断结点时否被搜索过，若未被搜索过，则进入该节点递归调用自身，向更深度搜索；若被搜索过，则p=p->next，向下一个相邻节点（另一条路）搜索，直到p为空时，循环结束，全部递归循环结束后，DFS完成。

#define MAXV 10//访问点数

int visited[MAXV] = { 0 };
void DFS(AdjGraph* G, int v)
{
	ArcNode* p;
	visited[v] = 1;                   //置已访问标记
	printf("%d  ", v); 				//输出被访问顶点的编号
	p = G->adjlist[v].firstarc;      	//p指向顶点v的第一条弧的弧头结点
	while (p != NULL)
	{
		if (visited[p->adjvex] == 0)	//若p->adjvex顶点未访问,递归访问它
			DFS(G, p->adjvex);
		p = p->nextarc;              	//p指向顶点v的下一条弧的弧头结点
	}
}

广度优先遍历(Breadth First Search，DFS)：

采用队列，创立一个遍历数组visited[vertex],未遍历的点赋值为0，已搜索过的点赋值为1。

先输出并进队起点，开始出队循环，出队队首，将队首的所有邻接点判断是否被遍历，若未被遍历依次输出并进队，这样不断循环完成BFS。

#include <queue>

void BFS(AdjGraph* G, int v)
{
	int w, i;
	ArcNode* p;
	queue<int> qu;							//定义队列
	int visited[MAXV];            			//定义顶点访问标志数组
	for (i = 0; i < G->n; i++) visited[i] = 0;		//访问标志数组初始化
	printf("%2d", v); 						//输出被访问顶点的编号
	visited[v] = 1;              				//置已访问标记
	qu.push(v);
	while (!qu.empty())   						//队不空循环
	{
		w = qu.front();
		qu.pop();					//出队一个顶点w
		p = G->adjlist[w].firstarc; 			//指向w的第一个邻接点
		while (p != NULL)						//查找w的所有邻接点
		{
			if (visited[p->adjvex] == 0) 		//若当前邻接点未被访问
			{
				printf("%2d", p->adjvex);  	//访问该邻接点
				visited[p->adjvex] = 1;		//置已访问标记
				qu.push(p->adjvex);		//该顶点进队
			}
			p = p->nextarc;              		//找下一个邻接点
		}
	}
	printf("\n");
}

如果不是连通图的话，则需要遍历visited数组，让还没搜索到的点继续遍历。

void DFS1(AdjGraph* G)//或者BFS1
{
	int i;
	for (i = 0; i < G->n; i++)
	{
		if (visited[i] == 0)
		{
			DFS(G, i);//或者BFS(G, i);
		}
	}
}

生成树和最小生成树：

生成树：

深度优先生成树（DFS Tree）

广度优先生成树（BFS Tree）

最小生成树：

普利姆算法(Prim)：适用于稠密图时间复杂度( $n^2$ ) (n为顶点数)

创建lowcost数组记录顶点集最短相邻边，closest数组记录顶点，先赋予数组初值，lowcost装当前顶点集的路径；然后找出剩余的n-1个顶点，每次比较顶点集的所有边，找出最短边，并赋值为0，说明已经加入顶点集，然后重新赋值新顶点产生的边到lowcost数组里，以及顶点closest里。直到循环结束，完成Prim算法。

void Prim(MatGraph g, int v)
{
	int lowcost[MAXV];			//顶点i是否在U中
	int min;
	int closest[MAXV], i, j, k;
	for (i = 0; i < g.n; i++)          //给lowcost[]和closest[]置初值
	{
		lowcost[i] = g.edges[v][i];
		closest[i] = v;
	}
	for (i = 1; i < g.n; i++)          //找出n-1个顶点
	{
		min = INF;
		for (j = 0; j < g.n; j++)       //在(V-U)中找出离U最近的顶点k
			if (lowcost[j] != 0 && lowcost[j] < min)
			{
				min = lowcost[j];
				k = j;			//k记录最近顶点的编号
			}
		printf(" 边(%d,%d)权为:%d\n", closest[k], k, min);
		lowcost[k] = 0;         	//标记k已经加入U
		for (j = 0; j < g.n; j++)   	//修改数组lowcost和closest
			if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])
			{
				lowcost[j] = g.edges[k][j];
				closest[j] = k;
			}
	}
	cout << endl;
}

克鲁斯卡尔算法(Kruskal)：适用于稀疏图时间复杂度( $e*log_{2} e$ ) (e为边数)

创建一个边Edge的数据结构收集边的信息（起点，终点，权值），并查集UFSTree（秩，双亲结点）

typedef struct
{
	int u;			//边的起始顶点
	int v;			//边的终止顶点
	int w;			//边的权值
} Edge;
typedef struct node
{
	int rank;						//结点对应秩
	int parent;						//结点对应双亲下标
} UFSTree;							//并查集树结点类型

有这些数据结构之后创立数组E和t，将MatGraph邻接矩阵中图的信息导入到边数组E中，对数组E按照权的大小进行排序(从小到大)，初始化数组t（将每个节点看成是一颗独立的树），用k记录录入的点，j记录到达的边，进入循环依次遍历所有边，每次录入边的起点和终点，并且并查集，找出起点和终点的根节点，如果它们的根节点不相同才能进行树的按秩合并（因为如果它们是一棵树上的结点，也就是说根节点相同的话，它们之间是可以相互到达的，没有必要再进行合并了）最终合并完n-1个顶点。

void Kruskal(MatGraph g)
{
	int i, j, k, u1, v1, sn1, sn2;
	UFSTree t[MaxSize];
	Edge E[MaxSize];
	k = 1;					//e数组的下标从1开始计
	for (i = 0; i < g.n; i++)		//由g产生的边集e
		for (j = 0; j <= i; j++)
			if (g.edges[i][j] != 0 && g.edges[i][j] != INF)
			{
				E[k].u = i; E[k].v = j; E[k].w = g.edges[i][j];
				k++;
			}
	HeapSort(E, g.e);		//采用堆排序对E数组按权值递增排序
	MAKE_SET(t, g.n);		//初始化并查集树t
	k = 1;               		//k表示当前构造生成树的第几条边,初值为1
	j = 1;               		//E中边的下标,初值为1
	while (k < g.n)       	//生成的边数小于n时循环
	{
		u1 = E[j].u;
		v1 = E[j].v;			//取一条边的头尾顶点编号u1和v2
		sn1 = FIND_SET(t, u1);
		sn2 = FIND_SET(t, v1); //分别得到两个顶点所属的集合编号
		if (sn1 != sn2)     	//两顶点属于不同的集合,该边是最小生成树的一条边
		{
			printf("  (%d,%d):%d\n", u1, v1, E[j].w);
			k++;			//生成边数增1
			UNION(t, u1, v1);	//将u1和v1两个顶点合并
		}
		j++;   				//扫描下一条边
	}
}

最短路径：

Dijkstra算法（迪杰斯特拉）：从一个顶点到其余个顶点的最短路径

形似于Prim算法，创立数组s表示当前的顶点集，dist数组表示起始顶点v到达其他顶点的最短距离，数组path用来记录路径。从起始顶点v出发，先初始化各个数组，然后将邻接矩阵中的值（顶点v的的边）录入到dist数组中，再根据数组S判断当前dist中最短路径是否加入顶点集，从未被加入顶点集的最短dist边，加入顶点集，然后再把这个顶点的出边与dist中的值进行比较，若短于当前的边，则将其录入相应的dist中，已经加入顶点集的点，则特殊值表示已经录入，S[i]=1，然后修改对应的path，使之指向该路径的前一个顶点，这样循环结束后，即可得到dist数组与path数组。

输出路径：输出从一个顶点到其余个顶点的最短路径，最短路径dist记录着其数值，path记录着路径，找到对应的path，上面提到了，它是指向前一个顶点，这样不断回溯，就找齐了最短路径所需路径。

void Dijkstra(MatGraph g, int v)	//Dijkstra算法
{
	int dist[MAXV], path[MAXV];//distance,path
	int S[MAXV];				//S[i]=1表示顶点i在S中, S[i]=0表示顶点i在U中
	int Mindis, i, j, u;
	for (i = 0; i < g.n; i++)
	{
		dist[i] = g.edges[v][i];	//距离初始化
		S[i] = 0;					//S[]置空
		if (g.edges[v][i] < INF)	//路径初始化
			path[i] = v;			//顶点v到顶点i有边时，置顶点i的前一个顶点为v
		else
			path[i] = -1;			//顶点v到顶点i没边时，置顶点i的前一个顶点为-1
	}
	S[v] = 1; path[v] = 0;			//源点编号v放入S中
	for (i = 0; i < g.n - 1; i++)		//循环直到所有顶点的最短路径都求出
	{
		Mindis = INF;				//Mindis置最大长度初值
		for (j = 0; j < g.n; j++)		//选取不在S中（即U中）且具有最小最短路径长度的顶点u
			if (S[j] == 0 && dist[j] < Mindis)
			{
				u = j;
				Mindis = dist[j];
			}
		S[u] = 1;					//顶点u加入S中
		for (j = 0; j < g.n; j++)		//修改不在S中（即U中）的顶点的最短路径
			if (S[j] == 0)
				if (g.edges[u][j] < INF && dist[u] + g.edges[u][j] < dist[j])
				{
					dist[j] = dist[u] + g.edges[u][j];
					path[j] = u;
				}
	}
}

Floyd算法（弗洛伊德）：每对顶点之间的最短路径

创建两个矩阵，一个最短路径矩阵A，一个路径矩阵path。先初始化（A相当于邻接矩阵，path中对应邻接矩阵，直接可达路径的则将路径的起点赋值到相应的path中，不直接可达赋值-1），然后从起点顶点开始，不断遍历顶点，借助该顶点，再遍历A中的所有最短路径，从i到j在借助已知最短路径和该顶点的出边能否以更短的路径到达，若能则替代，并将path中的对应的path[i][j]的值更改为路径终点j的前一个顶点。

输出路径：顶点i到顶点j之间的最短路径就是A[i][j]中的值，其路径就是path[i][j]中的对应的数字，也是不断地在path[i]中回溯，每次path的值就是所经过的顶点，直到起点，然后输出。

void Floyd(MatGraph g)							//Floyd算法
{
	int A[MAXV][MAXV], path[MAXV][MAXV];
	int i, j, k;
	for (i = 0; i < g.n; i++)
		for (j = 0; j < g.n; j++)
		{
			A[i][j] = g.edges[i][j];
			if (i != j && g.edges[i][j] < INF)
				path[i][j] = i;					//顶点i到j有边时
			else
				path[i][j] = -1;				//顶点i到j没有边时
		}
	for (k = 0; k < g.n; k++)						//依次考察所有顶点
	{
		for (i = 0; i < g.n; i++)
			for (j = 0; j < g.n; j++)
				if (A[i][j] > A[i][k] + A[k][j])
				{
					A[i][j] = A[i][k] + A[k][j];	//修改最短路径长度
					path[i][j] = path[k][j];		//修改最短路径
				}
	}
}

拓扑排序：按照有向图的顺序进行顶点的选择，这会产生不同的顺序，这些顺序就是拓扑排序。（在一个有向图中找一个拓扑排序的过程称为拓扑排序）

AOE网与关键路径：AOE网（activity on edge）叫做工程，顶点叫做事件，边叫做活动，根据拓扑排序以及拓扑排序逆序，在原有图上找到所有事件的最早开始时间ve（event early）,最迟开始时间vl（event late），然后根事件的时间找出每个活动的最早开始时间e，最迟开始时间l，活动的最早与最迟时间之差，如果为零，则为关键路径，因为没有时间可以多出来使用了。

第九章查找

ASL（平均查找长度(Average Search Length)）

线性表的查找：

顺序查找(SequentialSearch)[O(n)]、

折半查找(BinarySearch)[O( $\log_{2}n$ )]、

索引存储分块查找(BlockSearch)[O( $\log_{2}n$ )(按照 $\sqrt{n}$ 分块)]、

二叉排序树(BST树)（依次比根小左子树，比根大右子树，使用递归查找,删除补上左子树）、

平衡二叉树(AVL树)（特殊的二叉排序树，为了提高确保查找效率最坏也是O( $\log_{2}n$ )）

在二叉排序树的基础上，插入时确保左右平衡，控制树的高度，判断平衡因子(balance factor,bf)进行二叉树的调整；在删除时，和二叉排序树一样，但是需要进行调整。

红黑树（AVL需要牺牲插入，来提高查找效率，当多次插入时，为提高效率，采用红黑树）

B_树（B Tree）（根据B_树的阶m插入进行分裂，删除进行合并，查找O( $\log_{m} n$ )）

B+树（B_树的变形，查找需要到叶子节点，，应用到操作系统中）

哈希表（哈希冲突(开放定址法(线性探测法、平方探测法)，拉链法））

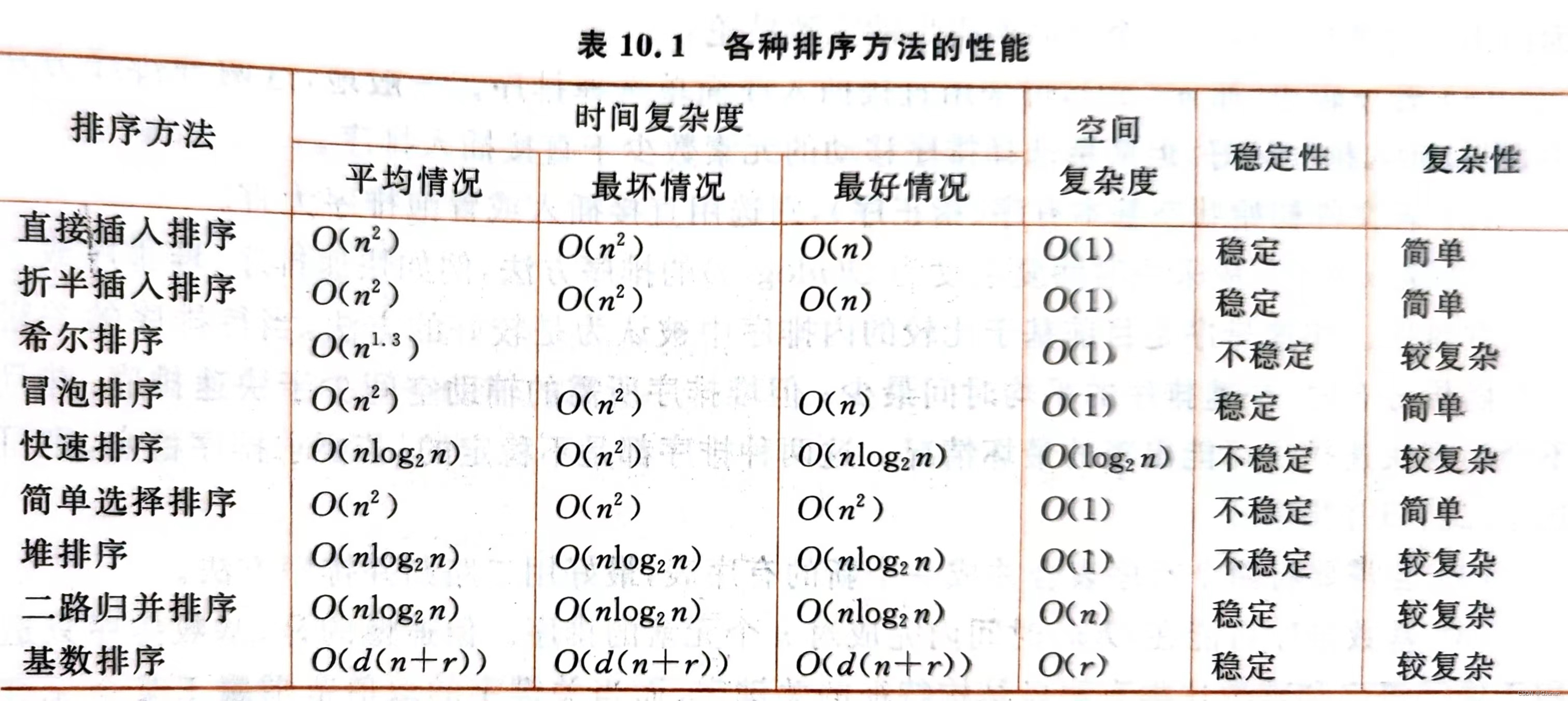
第十章内排序

插入排序（直接插入排序(O( $n^{2}$ ))、折半插入排序(O( $n^{2}$ ))、希尔排序(O( $n^{1.3}$ ))）

交换排序（冒泡排序(O( $n^{2}$ ))、快速排序(O( $n\log_{2}n$ ))、选择排序( O( $n^{2}$ ))、堆排序(O( $n\log_{2}n$ ))、

归并排序( O( $n\log_{2}n$ ))、基数排序(O(d(n+r)))

第十一章外排序

磁盘排序：多路平衡归并、最佳归并树

磁带排序：多路平衡归并排序、多阶段归并排序

第十二章文件

外存上的文件，常用文件组织方式：顺序文件、索引文件、哈希文件、多关键字文件……

第十三章采用面向对象的方法描述算法

熟练使用STL（Standard Template Library）

GJunan

关注

8
点赞
踩
46

收藏

觉得还不错? 一键收藏
1
评论
个人随意总结知识——数据结构教程（第5版）【李春葆】

个人随意总结知识——数据结构教程（第5版）【李春葆】前缀表达式中缀表达式后缀表达式 Brute-Force算法 KMP算法递归汉诺塔二叉树树遍历深度优先遍历 DFS 广度优先遍历 BFS 最小生成树 Prim算法 Kruskal算法 Dijkstra算法狄克斯特拉算法 Floyd算法弗洛伊德算法从一个顶点到其余个顶点的最短路径每对顶点之间的最短路径拓扑排序 AOE网查找内排序外排序
复制链接

扫一扫