网络流之最小割模型

狂暴刷题组长

已于 2023-04-13 00:51:50 修改

阅读量359

点赞数 2

分类专栏： # 算法学习笔记文章标签：算法 c++ 图论

于 2023-01-01 15:27:59 首次发布

本文链接：https://blog.csdn.net/GROZAX/article/details/128512825

版权

算法学习笔记专栏收录该内容

9 篇文章 1 订阅

订阅专栏

最小割模型通常用来解决可以转换成两个集合，并使相关条件转换成集合之间的流量的问题。

1、初始模板（Dinic算法）

给定一个包含 n 个点 m 条边的有向图，并给定每条边的容量，边的容量非负。

图中可能存在重边和自环。求从点 S 到点 T 的最小割。

由于最大流最小割定理我们可以证明出最小割 = 最大流，所以求最小割也就相当于求最大流。用一遍dinic算法即可。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = 200020, INF = 1e8;

int e[M], ne[M], h[N], fc[M], idx;
int n, m, S, T;
int q[N], cur[N], d[N];

void add(int a, int b, int c) {
    e[idx] = b; fc[idx] = c; ne[idx] = h[a]; h[a] = idx++;
    e[idx] = a; fc[idx] = 0; ne[idx] = h[b]; h[b] = idx++;
}

bool bfs() {
    int hh = 0, tt = 0;
    memset(d, -1, sizeof d);
    q[0] = S; d[S] = 0; cur[S] = h[S];
    
    while (hh <= tt) {
        int t = q[hh++];
        for (int i = h[t]; ~i; i = ne[i]) {
            int ver = e[i];
            if (d[ver] == -1 && fc[i]) {
                d[ver] = d[t] + 1;
                cur[ver] = h[ver];
                if (ver == T) return true;
                q[++tt] = ver;
            }
        }
    }
    return false;
}

int find(int u, int limit) {
    if (u == T) return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
        cur[u] = i;
        int ver = e[i];
        if (d[ver] == d[u] + 1 && fc[i]) {
            int t = find(ver, min(fc[i], limit - flow));
            if (!t) d[ver] = -1;
            fc[i] -= t; fc[i ^ 1] += t; flow += t;
        }
    }
    return flow;
}

int Dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = find(S, INF)) res += flow;
    return res;
}

int main() {
    cin >> n >> m >> S >> T;
    memset(h, -1, sizeof h);
    while (m--) {
        int u, v, c;
        cin >> u >> v >> c;
        add(u, v, c);
    }
    cout << Dinic();
    
    return 0;
}

2、分数规划问题

给出一个带权无向图 G=(V,E)，每条边 e 有一个权 w。

求将点 s 和点 t 分开的一个边割集 C，使得该割集的平均边权最小，即最小化：

$\frac{\sum_{e\epsilon C}w_e}{|C|}$

注意： 边割集的定义与最小割中的割边的集合不同。在本题中，一个边割集是指：将这些边删去之后，s 与 t 不再连通。

对于分数规划问题，我们可以设 $\large \lambda =\frac{\sum_{e\epsilon C}w_e}{|C|}$ ，其中 $\large \lambda$ 为我们要求的理论最小值。

3、最大权闭合图

闭合图：在有向图中，我们选取一些点构成集合，记为G(u, v)，且集合中的点的出边，所指向的终点也在G中，则我们称这个集合为闭合图。

最大权闭合图即在所有闭合图中，点的权值之和最大的集合。

试想一个选课方案，每一门课都有若干前置课需要学习，那么我们可以从这门课连一条指向前置课的边，闭合图即为选取若干课为一个集合，这些课不再需要集合外的课作为前置课。如果每门课都有不同的学分，那么最大权闭合图即为总学分最多的闭合图。

~~根据这篇博客的题目我们知道这样的题目可以转换成最小割模型。~~

如何把最大权闭合图转化为最小割的模型？

先引入一个简单割的概念：在一个割中，如果连接两个集合的边都是源点或者汇点的邻边，那么这个割被称为简单割。（这个概念仅限最大权闭合图内部证明使用）

那么不难证明最小割一定是简单割：

（此处省略证明步骤）

我们可以围绕闭合图建立如下的流网络G：

1、将源点S与闭合图中 $w_i>0$ 的点连接，流量为 $w_i$ ；

2、将闭合图中 $w_i<0$ 的点与汇点连接，流量为 $-w_i$ ；

3、闭合图内部的边流量为 INF。

设图中的闭合图点集 $V_1$ ，除了闭合图的其他点集为 $V_2$ ；

那么将 $V_1V_2$ 分别划分到两个集合的简单割的容量就由四种边构成：

$V_1\rightarrow V_2$ 、 $V_1\rightarrow T$ 、 $S\rightarrow V_2$ 、 $S\rightarrow T$

由闭合图以及简单割的定义我们知道 $V_1\rightarrow V_2$ 和 $S\rightarrow T$ 这两种边不存在，所以我们可以将割的容量表示为

$\large c(S, T) = c(S,\{V_2\})+ c(\{V_1\},T)$

.

$\large = \sum_{u \epsilon V_2^+}{w(u)} + {\color{Red} \sum_{v \epsilon V_1^-}{-w(v)}}$

而我们要求的闭合图的最大权

$\large w(V_1) = \sum_{ u\epsilon V_1^+}{w(u)} + \sum_{v \epsilon V_1^-}{w(v)}$

.

$\large = \sum_{ u\epsilon V_1^+}{w(u)} - {\color{Red} \sum_{v \epsilon V_1^-}{-w(v)}}$

两式相加，红色部分可以消掉

$\large c(S, T)+w(V_1) =\sum_{u \epsilon V_2^+}{w(u)} + \sum_{ u\epsilon V_1^+}{w(u)} = w(V^+)$

.

移项，得 $\large {\color{Teal}w(V_1) = w(V^+)-c(S, T)}$

由于所有正权点和为定值，所以要让闭合图的权最大，即让割的容量最小，即求出最小割，证毕。

4、最大密度子图

对于一个无向图，密度D为该图的边数|E|与该图的点数|V|的比值，即 $\small D=\frac{|E|}{|V|}$ ，具有最大比值的子图被称为最大密度子图

(1)、模型转换解法

根据分数规划问题的思路，我们可以将公式变式：

设 $\small D' = \frac{|E'|}{|V'|}$ 为最大密度， $|V'|- D'\times |E'|= 0$

设函数 $g(x)=|V'|- x\cdot |E'|$ ，且 $g(x^*)=0$

那么g(x)满足

$\left\{\begin{matrix}g(x) = 0,x=x^* \\ g(x)<0,x>x^* \\ g(x)>0,x<x^* \end{matrix}\right.$

那么我们就可以用二分查找x*的具体值。

如果我们把每条边都看做一个点，这个点连接边的两个端点，要使D最大，则让|E|尽可能大，|V|尽可能小，也就是点权值尽可能大，那么这个图也就转换成了求闭合图中的最大权问题。

具体做法是：设猜测值为g，则将边转化成的点权为1，原来的点为-g建立闭合图，然后按照求最大权闭合图的方式求解即可。时间复杂度为 $O(logn\cdot MaxFlow(n+m,n+m))$ 。

很明显复杂度有点高，我们看看是否能从最大密度子图的性质入手优化算法。

(2)、优化算法

仔细观察原问题h(g)，在点的数量固定的情况下，我们要尽量选择更多的边，也就是说

对于图G的子图，在点集固定的情况下，取点集的导出子图的边集E'，显然是最优解

导出子图(induced subgraph)：由该图顶点的一个子集和该图中两端均在该子集的所有边的集合组成的图。

它要让密度最大，即最大化 $|E'|-g\cdot |V'|$ ，相当于最小化 $g\cdot |V'|-|E'|$ ，为了导出子图里边的数量，我们可以把每条边拆成两份，分别给两边的端点所有，那么导出子图里边的数量就是所有点度数减去出去边的，但是每条边被拆成了两份，所以再除以2，也就是

$\large g\cdot |V'|-|E'|= \sum_{v\epsilon V'}g -(\frac{\sum_{v\epsilon V'}d_v}{2}-\frac{c(V',\overline{V'})}{2})$

提取求和符号并把割集独立

$\large = \sum_{v\epsilon V'}(g -\frac{d_v}{2})+\frac{c(V',\overline{V'})}{2}$

再提出系数1/2

$\large = \frac{1}{2}(\sum_{v\epsilon V'}(2g -d_v)+c(V',\overline{V'}))$

对于这个式子，如果我们能把前面的一坨放到割里面就好了，这样只需要求新图最小割的一半即可。

那么我们按照这个想法建图：将所有的点连接一条容量为 $2g-d_v$ 的边到T，代表是否选择这条边，由于 $2g-d_v$ 有可能是负数，所以统一加上一个大常数U，那么就可以从源点S连接每一个点，容量为U，点和点之间的容量都为1。

（加上常数的证明在此处补充）

接下来证明一下是否与题意等价。

对于新图的割有四种包含的边： $V'\rightarrow \overline{V'},V'\rightarrow T,S\rightarrow \overline{V'},S\rightarrow T$

已知我们连边的方式是不会存在 $S\rightarrow T$ 这条边的

所以新图的割：

$\large c(S,T)=\sum_{u\epsilon V'} \sum_{v\epsilon \overline{V'}} w(u,v)+ \sum_ {u\epsilon V'}(2g-d_u+U)+ \sum_{v\epsilon \overline{V'}}U$

提出U

$\large =\sum_{u\epsilon V'} \sum_{v\epsilon \overline{V'}} w(u,v)+\sum_ {u\epsilon V'}(2g-d_u)+ \sum_{v\epsilon V'}U+\sum_{v\epsilon \overline{V'}}U$

将前两项提取求和符号并将后两项合并

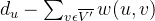
$\large =\sum_{u\epsilon V'} (2g-d_u+\sum_{v\epsilon \overline{V'}} w(u,v))+ U\cdot n$

注意 $d_u-\sum_{v\epsilon \overline{V'} }w(u,v)$

这个式子代表的含义是对于V'集合内的点u，它的所有邻边减去所有连向集合 $\overline{V'}$ 的边，也就等于集合V'内部的边，所以

$\large d_u-\sum_{v\epsilon \overline{V'} }w(u,v)=\sum_{v\epsilon V' }w(u,v)$

回到原式

将我们刚才的推导带入

    $\large =\sum_{u\epsilon V'} (2g-\sum_{v\epsilon V'} w(u,v))+ U\cdot n$

再将括号展开

   $\large =2g\sum_{u\epsilon V'} -\sum_{u\epsilon V'} \sum_{v\epsilon V'} w(u,v)+ U\cdot n$

由于我们设立的图内部的边权为1，所以 $w(u,v) = 1$ ，剩下的用集合来替代求和

   $\large =2g\cdot |V'|-2|E'|+U\cdot n$

提取系数2

   $\large =2(g\cdot |V'|-|E'|)+U\cdot n$

我们最终的目的是为了最小化 $g\cdot |V'|-|E'|$ ，而系数2和常数U为定值，所以等价于求 $c(S,T)$ 的最小值，也就是求最小割，证毕。

建立模型总结：从起点连接一条容量为U的边到所有点，从所有点连接一条容量为 $2g-d_u+U$ 的边到T，点之间的边容量为1。最终的结果为最小割减去U*n再除以2。

例题：生活的艰辛

约翰是一家公司的 CEO。

公司的股东决定让他的儿子斯科特成为公司的经理。

约翰十分担心，儿子会因为在经理岗位上表现优异而威胁到他 CEO 的位置。

因此，他决定精心挑选儿子要管理的团队人员，让儿子知道社会的险恶。

已知公司中一共有 n 名员工，员工之间共有 m 对两两矛盾关系。

如果将一对有矛盾的员工安排在同一个团队，那么团队的管理难度就会增大。

一个团队的管理难度系数等于团队中的矛盾关系对数除以团队总人数。

团队的管理难度系数越大，团队就越难管理。

约翰希望给儿子安排的团队的管理难度系数尽可能大。

请帮帮他。

以上图为例，管理难度系数最大的团队由 1,2,4,5 号员工组成，他们 4 人中共有 5 对矛盾关系，所以管理难度系数为 5/4。

如果我们将 3 号员工也加入到团队之中，那么管理难度系数就会降至 6/5。

5、最小权覆盖集

点覆盖集（VCS）：在无向图中点集的一个子集V，使得图中所有边都至少有一个端点在V内，则集合V是原图的一个点覆盖集。

由于最小权覆盖集和后面要讲的最大权独立集都是NP问题，也就是被证明只能用暴搜求解的问题，所以我们这里讨论的图均为二分图。

在二分图一章中，我们使用了匈牙利算法来求解无点权的最小点覆盖集问题，但是如果每个点都有权值，并且要使最后的点覆盖集的权值和最小，那么匈牙利算法就无法解决了，我们考虑是否能够转化成最小割模型来求解。

建立流网络的方式和最大流二分图匹配一致，不同的是从源点S到左列点的边流=左列点权，右列点到汇点T的边流=右列点权，左右列的边流均设为INF。如图所示：

这里我们需要证明两个命题：

1、最小割一定是简单割

反证法，如果最小割不是简单割，则说明最小割有一条两端既不是源点也不是汇点的边，也就是左列连向右列的边权为INF的边，那么这个割的容量即为INF，与最小割定义矛盾。

2、点覆盖集与简单割一一对应（双射）（这里的点覆盖集保证没有冗余点）

(1)、简单割 $\Rightarrow$ 点覆盖集

对于建立的流网络，如果简单割的割边包含S，则把与之连接的左列点加入集合，如果各边包括T，则把连接T的右列点加入集合，最后这个集合一定是点覆盖集。

反证：如果不是点覆盖集，说明有一条边的两个端点u, v都不在我刚才建立的集合里，那么我们就可以通过连接一条 $S\rightarrow u\rightarrow v\rightarrow T$ 的路径让S和T连接，这与我们割的定义S和T在两个不同的集合里相矛盾。

(2)、点覆盖集 $\Rightarrow$ 简单割

对于任意一个点覆盖集，我们可以把左列的点与s相连的边删掉，把右列点与t相连的边删掉，那么对于新图G'，从s开始进行dfs搜索，能够走到的点放在集合S里，剩下的点放在集合T里。那么这样建立的是不是简单割呢？

反证：如果我们能够从s走到t，说明我们走过了中间的某一条边，那么这条边的两个端点均不再点覆盖集内，这与覆盖集的定义矛盾，所以我们建立的一定是割，并且我们删除的割边都是与s或t相连的边，所以我们建立的一定是简单割。

综上：点覆盖集与简单割能够一一对应。点覆盖集的点权和即是对应简单割的容量。

那么我们只需要对整个网络求最小割，通过上面两个命题我们即可证明这个最小割与最小权覆盖集相等。

6、最大权独立集

点独立集（VIS）：在无向图中点集的一个子集V，V中的任意两点都不相邻，则集合V是原图的一个点独立集。

覆盖集与独立集互补定理：对于无向图的任意一个覆盖集V，它的补集V'是原图的一个独立集，反之亦然。

证明：

(1)、覆盖集V的补集V'一定是独立集

反证：如果V'不是独立集，则说明V'中存在两个点相邻，那么V中不包括这两个相邻点，也就不包括这条边，与覆盖集定义矛盾。

(2)、独立集V'的补集V一定是覆盖集

反证：如果V不是覆盖集，则说明原图中有某条边的两个端点均不在V中，那么V'则都包括这两个端点，与独立集的定义矛盾。

综上，覆盖集与独立集互补。

设某个独立集V和它的补集V'，因为V + V' = U，V = U - V'；

由于全体点权和U为定值，所以要求最大化V，则求出最小化V'，也就是最小权覆盖集即可。

之后的问题转化成求最小割即可。