算法训练一（贪心、二分）（含解题思路）（下）

清晨喝碗粥

于 2022-10-28 14:42:50 发布

阅读量1.4k

点赞数 1

分类专栏： PTA 文章标签：算法 c++ 学习

本文链接：https://blog.csdn.net/G_matinal/article/details/127569623

版权

PTA 专栏收录该内容

12 篇文章

订阅专栏

7-18简简单单的数学题（位运算 + 哈希表）

因题集题目较多，前一半题解请移步这里

算法训练一（贪心、二分）（含解题思路）_清晨喝碗粥的博客-CSDN博客

7-15种树（贪心）

一条街道的一边有几座房子。因为环保原因居民想要在路边种些树，路边的地区被分割成n块，并被编号为1…n，每块大小为一个单位尺寸并最多可种一棵树。每个居民想在门前种些树并指定了三个数b，e，t这三个数分别表示该居民想在b和e之间最少种t棵树，当然，b≤e，t≤e-b+1，允许居民想种树的子区域可以交叉。出于资金紧缺的原因，环保部门请你求出能够满足所有居民的种树要求时所需要种的树的最少数量。

输入格式：

第一行为n，表示区域的个数。

第二行为h，表示房子的数目。

下面h行描述居民的需要：b、e、t(0<b≤e≤30 000，t≤e-b+1)分别用一个空格分开。

输出格式：

输出一个数，为满足所有居民的要求，所需要种树的最少数量。

输入样例：

9
4
1 4 2
4 6 2
8 9 2
3 5 2

输出样例：

5

数据规模：

30%的数据满足 0<n≤l 000；0<h≤500。
100%的数据满足 n≤30 000；h≤5 000, 0<b≤e≤30 000，t≤e-b+1。

思路：首先将区间按照右端点从小到大排序，因为题干要求所种树的最少数量，所以我们需要尽最大努力将树种在公共区域，我们可以选择集中在区间右端，重叠部分做一个标记，若可以种树，则该区间所需树减一

AC代码：

#include<bits/stdc++.h>
using namespace std;
bool cmp(vector<int>a, vector<int>b) {
    if (a[1] == b[1])
        return a[0] < b[0];
    return a[1] < b[1];
}
int main()
{
    int i, j, n, t, count = 0;
    cin >> n >> t;
    vector<bool>temp(n, false);
    vector<vector<int>>nums(t, vector<int>(3, 0));
    for (i = 0; i < t; i++) {
        for (j = 0; j < 3; j++) {
            cin >> nums[i][j];
        }
    }
    sort(nums.begin(), nums.end(), cmp);
    for (i = 0; i < t; i++) {
        for (j = nums[i][0]; j <= nums[i][1] && nums[i][2] > 0; j++) {
            if (temp[j]) {
                nums[i][2]--;
            }
        }
        for (j = nums[i][1]; j >= nums[i][0] && nums[i][2] > 0; j--) {
            if (!temp[j]) {
                temp[j] = !temp[j];
                nums[i][2]--;
                count++;
            }
        }
    }
    cout << count << endl;

    system("pause");
    return 0;
}

7-16会场安排问题（贪心）

题目来源：王晓东《算法设计与分析》

假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。设计一个有效的
贪心算法进行安排。（这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个
顶点，不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数，相应于要找的最小
会场数。）

输入格式：

第一行有 1 个正整数k，表示有 k个待安排的活动。
接下来的 k行中，每行有 2个正整数，分别表示 k个待安排的活动开始时间和结束时间。时间
以 0 点开始的分钟计。

输出格式：

输出最少会场数。

输入样例：

5
1 23
12 28
25 35
27 80
36 50

输出样例：

3

思路：简化版的7-12，在7-12的基础上可以放弃对每一组数据进行标记招新宣讲会的个数即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, j, k, n;
    cin >> n;
    vector<vector<int>>nums(n, vector<int>(2, 0));
    for (i = 0; i < n; i++) {
        cin >> nums[i][0] >> nums[i][1];
    }
    sort(nums.begin(), nums.end()), [](vector<int>a, vector<int>b) {
        return a[1] < b[1];
    };
    priority_queue<int, vector<int>, greater<int>>Q;
    i = 0;
    while (i < n) {
        if (!Q.empty() && nums[i][0] >= Q.top())
            Q.pop();
        Q.push(nums[i][1]);
        i++;
    }
    cout << Q.size() << endl;

    system("pause");
    return 0;
}

7-17最优合并问题（贪心）

题目来源：王晓东《算法设计与分析》

给定k 个排好序的序列, 用 2 路合并算法将这k 个序列合并成一个序列。
假设所采用的 2 路合并算法合并 2 个长度分别为m和n的序列需要m+n-1 次比较。试设
计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最少。
为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最多。

输入格式：

第一行有 1 个正整数k，表示有 k个待合并序列。
第二行有 k个正整数，表示 k个待合并序列的长度。

输出格式：

输出最多比较次数和最少比较次数。

输入样例：

4
5 12 11 2

输出样例：

78 52

思路：先对序列进行排序，最多比较次数：每次合并时选最长两个，最少比较次数：每次合并时选最短的两个。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int solve_max (vector<int> &nums) {
    priority_queue<int, vector<int>, less<int>>Q;
    int i, cur = 0, res = 0;
    while (cur < nums.size()) {
        Q.push(nums[cur++]);
    }
    while (Q.size() > 1) {
        int item = 0;
        for (i = 0; i < 2; i++, Q.pop()) {
            item += Q.top();
        }
        res += item - 1;
        Q.push(item);
    }
    return res;
}
int solve_min (vector<int> &nums) {
    priority_queue<int, vector<int>, greater<int>>Q;
    int i, cur = 0, res = 0;
    while (cur < nums.size()) {
        Q.push(nums[cur++]);
    }
    while (Q.size() > 1) {
        int item = 0;
        for (i = 0; i < 2; i++, Q.pop()) {
            item += Q.top();
        }
        res += item - 1;
        Q.push(item);
    }
    return res;
}
int main()
{
    int i, j, k, n, res_maxx, res_minn;
    cin >> n;
    vector<int>nums(n, 0);
    for (i = 0; i < n; i++) {
        cin >> nums[i];
    }
    res_minn = solve_min(nums);
    res_maxx = solve_max(nums);
    cout << res_maxx << " " << res_minn << endl;

    system("pause");
    return 0;
}

7-18简简单单的数学题（位运算 + 哈希表）

刘笑笑最近在准备考研，刘笑笑的高数很厉害。今天他不想做复杂的高数题，但是他每天要完成一道数学题，为什么？因为生活需要仪式感！！！

现在他手上有一个 n 个数的数组，他需要在 n 个数中取两个数(可以相同)使得他们异或最大。但他觉得这样子只知道答案没有仪式感，所以他想知道两个数中最小的下标是多少

输入格式：

第一行包含一个数 n 表示数字长度 (1<=n<=5e5)

第二行包含 n 个数 ai 表示数组 (1<=ai<=1e9)

输出格式：

输出一个数，表示异或最大的两个数中，最小的下标是多少。

输入样例：

2
1 2

输出样例：

1

思路：假设我们在数组中选择了元素nums[i]和nums[j]（I ≠ j），使得他们达到最大的按位异或运算结果x：x = nums[i] ^ nums[j]，我们首先想到的是利用双重循环去枚举，但其时间复杂度为O(N^2)，显然容易造成超时，所以我们不得不换一种思路，也就是位运算，我们可以思考异或运算的性质，x = nums[i] ^ nums[j] 等价于 nums[j] = x ^ nums[i]

这里浅浅证明一下：假设a ^ b = c, 此时我们将等式两边同时异或a，即a ^ a ^ b = c ^ a，因为a ^ a = 0, 所以b = c ^ a;

因为两两异或会得到一个值，又因为在所有的两两异或的值中总会有一个最大值，我们可以推测这个最大值，即根据这个最大值一点存在去解题。

我们于是就可以利用这个性质进行运用，首先我们看数组内元素是不超int（4字节）类型的，所以也就是31位二进制数（如果不满31位则在最高位之前补零），我们想求最大值，那么我们需要尽可能的在尽量高的位上寻找1，于是，我们可以假设高位上有这样一个1，然后把这n个数都遍历一遍，看看这一位是不是真的可以是1，否则就是0（假设数组内所有数的同等高位上均为1，那么任意随机选两个数在这一位异或均为0，那就找不到最大值了，所以当我们贪心的寻找最高位的1时还需要判断存在其他数在这一位上为0），如果a ^ b = max，那么a = b ^ max一定成立，所以我们可以把这n个数的前缀（掩码）进行异或运算并放到一个哈希表中，然后再遍历这些前缀，如果有一个数它与我们贪心假设的“最大值”异或恰巧能在哈希表中查询的到，那么这个数位上可能就是1，否则就是0，我们可以利用一个变量记录这个值的下标（如果能查询到），最后我们的下标一定是这个数组内两个数异或最大值的其中一个数（即nums[i] ^ nums[j] = max，下标记录的一定是nums[i]和nums[j]中的其中一个），最后在遍历一次寻找另一个数的下标即可。

如何得到前缀，即以掩码形式（如下）：

10000000000000000000000000000000

11000000000000000000000000000000

11100000000000000000000000000000

11110000000000000000000000000000

11111000000000000000000000000000

11111100000000000000000000000000

11111110000000000000000000000000

11111111000000000000000000000000

11111111100000000000000000000000

11111111110000000000000000000000

11111111111000000000000000000000

11111111111100000000000000000000

11111111111110000000000000000000

11111111111111000000000000000000

11111111111111100000000000000000

11111111111111110000000000000000

11111111111111111000000000000000

11111111111111111100000000000000

11111111111111111110000000000000

11111111111111111111000000000000

11111111111111111111100000000000

11111111111111111111110000000000

11111111111111111111111000000000

11111111111111111111111100000000

11111111111111111111111110000000

11111111111111111111111111000000

11111111111111111111111111100000

11111111111111111111111111110000

11111111111111111111111111111000

11111111111111111111111111111100

11111111111111111111111111111110

11111111111111111111111111111111

本方法仅阅读文字理解起来可能有点困难，可以参考下列代码及注释理解

AC代码：

#include<bits/stdc++.h>
using namespace std;
//最高位的二进制位编号为 30
#define HIGH_BIT 30
int main()
{
    int i, j, k, n, index1, index2;
    bool flag = true;
    cin >> n;
    vector<int>nums(n, 0);
    for (i = 0; i < n; i++) {
        cin >> nums[i];
    }
    int x = 0;
    for (k = HIGH_BIT; k >= 0; k--) {
        unordered_set<int>seen;
		//将所有的nums[j]前缀放入哈希表中
        for (i = 0; i < n; i++) {
			//如果只想保留从最高位开始到第 k 个二进制位为止的部分
			//只需将其右移 k 位
            seen.insert(nums[i] >> k);
        }

		//目前 x 包含从最高位开始到第 k+1 个二进制位为止的部分
		//我们将 x 的第 k 个二进制位置为 1，即为 x = x*2+1
        int x_next = x * 2 + 1;
        bool found = false;

		//枚举i
        for (i = 0; i < n; i++) {
            if (seen.count(x_next ^ (nums[i] >> k))) {
                index1 = i;
                found = true;
                break;
            }
        }

		//如果没有找到满足等式的nums[i] 和 nums[j]，那么 x 的第 k 个二进制位只能为 0
		//即为 x = x*2
        if (found)
            x = x_next;
        else 
            x = x_next - 1;
    }
	
	//找另一个数的下标
    int maxx = INT_MIN;
    for (i = 0; i < nums.size(); i++) {
        if ((nums[i] ^ nums[index1]) > maxx) {
            maxx = nums[i] ^ nums[index1];           
            index2 = i;
        }
    }
    cout << min(index1, index2) + 1 << endl;

    system("pause");
    return 0;
}

7-19h1489.田忌赛马（贪心）

这是一个编程题模板。

这是中国历史上的一个著名故事。

大约 2300 年前，田忌是齐国的一位将军，他喜欢与国王等人赛马。

田忌和国王都有三匹不同等级的马----下马、中马、上马。

规则是一场比赛要进行三个回合，每匹马进行一回合的较量，单回合的获胜者可以从失败者那里得到 200 银元。

比赛的时候，国王总是用自己的上马对田忌的上马，中马对中马，下马对下马。

由于国王每个等级的马都比田忌的马强一些，所以比赛了几次，田忌都失败了，每次国王都能从田忌那里拿走 600 银元。

田忌对此深感不满，直到他遇到了著名的军事家孙膑，利用孙膑给他出的主意，田忌终于在与国王的赛马中取得了胜利，拿走了国王的 200 银元。

其实胜利的方法非常简单，他用下马对战国王的上马，上马对战国王的中马，中马对战国王的下马，这样虽然第一回合输了，但是后两回合都胜了，最终两胜一负，取得了比赛胜利。

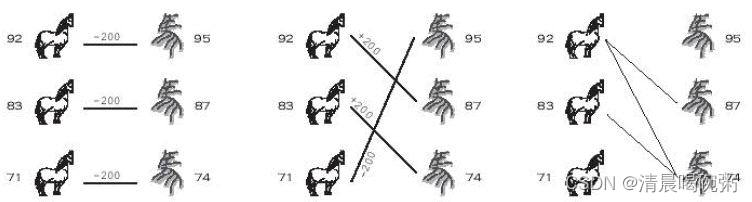
如果田忌活在如今，那么他可能会嘲笑自己当初的愚蠢。

重要的是，如果他现在正参加 ACM 竞赛，他可能会发现赛马问题可以简单地看作是在二分图中找到最大匹配项。

在一侧画田忌的马，在另一侧画国王的马，只要田忌的一匹马能够击败国王的一匹马，我们就在这两匹马之间画一条边。

然后，赢尽可能多的回合，就变成了在这个二分图中找到最大匹配。

如果存在平局，问题会变得更加复杂，他需要为所有可能的边分配权重 0、1 或 −1，并找到最大加权的完美匹配…

然而，赛马问题其实是二分图匹配的一种非常特殊的情况。

该图由马的速度决定，速度快的总是能击败速度慢的。

这种情况下，加权二分图匹配算法就显得大材小用了。

在这个问题中，你需要编写一个程序，来解决这一特殊的匹配问题。

输入格式：

输入包含最多 50 组测试数据。

每组数据第一行包含一个整数 n(1≤n≤1000)，表示一方马的数量。

第二行包含 n 个整数，是田忌的马的速度。

第三行包含 n 个整数，是国王的马的速度。

输入的最后一行为 0，表示输入结束。

输出格式：

每组数据输出一个占一行的整数，表示田忌最多可以获得多少银元

输入样例：

3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18

0

输出样例：

200
0
0

思路：

分类讨论即可，如果田忌的快马慢于国王的快马，则田忌要用慢马去输掉这一场，如果田忌的快马要快于国王的快马，则田忌要用自己的快马赢得这场比赛，这两种情况比较好理解，下面要提一下第三种情况，当国王的快马和田忌的快马一样快的时候，如果我们让田忌的快马对战国王的快马，有可能不是最优解（例如田忌的马的速度数组是[20, 30]，国王的是[25, 30]，那么田忌的最优解并不是让自己的快马去和国王快马比，这样的总得分是-200；他应该让自己的慢马去比，这样总得分是0，更优），所以我们要进行额外的判断，

1、如果田忌的慢马比国王的慢马快，那么田忌果断要让自己的慢马去对战国王的慢马，以发挥他慢马的效益。

2、如果田忌的慢马比国王的慢马慢，那他的慢马怎么比都要输，所以可以让它去和国王的快马去比，最大程度消耗对手。

3、如果田忌的慢马与国王的慢马一样快，那么就有两种考虑，要么让它去消耗国王的快马，要么让它去和国王慢马比。我们仔细考虑这两种可能性。首先田忌的这个慢马不会和别的马去比，如果它和国王的一个非最快也非最慢的马去比的话，那这匹马必输，那不如去和国王最快马比更优，所以田忌最慢马只会和国王的最快或者最慢马比。如果某个最优解里，田忌最慢马是和国王最慢马比的，那么考虑国王最快马是和田忌的哪个马比的，把田忌的那匹马挑出来和国王最慢马比，然后把田忌最慢马和国王最快马比，这样田忌的收益不会变得更差（如果田忌那匹马输了，那么这样交换后田忌有可能免于-200的输钱，也有可能收益不变；如果田忌那匹马没输，即平手，那么交换后收益没有变化）。总而言之，田忌仍然要把最慢马与国王最快马去比

AC代码：

#include<bits/stdc++.h>
using namespace std;
int solve(int n) {
    int i, j, count = 0, mon = 0;
    vector<int>nums1(n, 0), nums2(n, 0);
    for (i = 0; i < n; i++) {
        cin >> nums1[i];
    }
    for (i = 0; i < n; i++) {
        cin >> nums2[i];
    }
    sort(nums1.begin(), nums1.end());
    sort(nums2.begin(), nums2.end());
    int l1 = 0, l2 = 0, r1 = n - 1, r2 = n - 1;
    while (l1 <= r1) {
        if (nums1[r1] > nums2[r2]) {
            r1--;
            r2--;
            mon += 200;
        } else if (nums1[r1] < nums2[r2]) {
            l1++;
            r2--;
            mon -= 200;
        } else {
            if (nums1[l1] > nums2[l2]) {
                mon += 200;
                l1++;
                l2++;
            } else {
                if (nums1[l1] < nums2[r2])
                    mon -= 200;
                l1++;
                r2--;
            }
        }
    }
    return mon;
}
int main()
{
    int i, j, k, t;
    cin >> t;
    vector<int>res;
    while (t != 0) {
        res.push_back(solve(t));
        cin >> t;
    }
    for (i = 0; i < res.size(); i++) {
        cout << res[i] << endl;
    }

    system("pause");
    return 0;
}

7-21二分查找（二分）

输入n值(1<=n<=1000)、n个非降序排列的整数以及要查找的数x，使用二分查找算法查找x，输出x所在的下标（0~n-1）及比较次数。若x不存在，输出-1和比较次数。

输入格式：

输入共三行：
第一行是n值；
第二行是n个整数；
第三行是x值。

输出格式：

输出x所在的下标（0~n-1）及比较次数。若x不存在，输出-1和比较次数。

输入样例：

4
1 2 3 4
1

输出样例：

0
2

思路：简单二分，直接上代码了

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, l, r, n, x, item, count = 0;
    cin >> n;
    vector<int>nums(n, 0);
    for (i = 0; i < n; i++) {
        cin >> nums[i];
    }
    cin >> x;
    l = 0, r = nums.size() - 1;
    while (l <= r) {
        item = (l + r) / 2;
        count++;
        if (nums[item] == x) {
            break;
        }
        if (nums[item] > x)
            r = item - 1;
        else
            l = item + 1;
    }
    if (l > r) {
        cout << -1 << endl << count << endl;
    } else {
        cout << item << endl << count << endl;
    }

    system("pause");
    return 0;
}

7-22改写二分搜索算法（二分）

题目来源：《计算机算法设计与分析》，王晓东

设a[0:n-1]是已排好序的数组，请改写二分搜索算法，使得当x不在数组中时，返回小于x的最大元素位置i和大于x的最小元素位置j。当搜索元素在数组中时，i和j相同，均为x在数组中的位置。

输入格式：

输入有两行：

第一行是n值和x值；
第二行是n个不相同的整数组成的非降序序列，每个整数之间以空格分隔。

输出格式：

输出小于x的最大元素的最大下标i和大于x的最小元素的最小下标j。当搜索元素在数组中时，i和j相同。
提示：若x小于全部数值，则输出：-1 0
若x大于全部数值，则输出：n-1的值 n的值

输入样例：

6 5
2 4 6 8 10 12

输出样例：

1 2

思路：相比于上一题需要注意一下边界问题

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, l, r, n, x, item, count = 0;
    cin >> n >> x;
    vector<int>nums(n, 0);
    for (i = 0; i < n; i++) {
        cin >> nums[i];
    }
    if (x < nums[0]) {
        cout << -1 << " " << 0 << endl;
        return 0;
    }
    if (x > nums[n - 1]) {
        cout << nums[n - 2] << " " << nums[n - 1] << endl;
        return 0;
    }
    l = 0, r = nums.size() - 1;
    while (l <= r) {
        item = (l + r) / 2;
        count++;
        if (nums[item] == x) {
            break;
        }
        if (nums[item] > x)
            r = item - 1;
        else
            l = item + 1;
    }
    if (l > r) {
        cout << r << " " << l << endl;
    } else {
        cout << item << " " << item << endl;
    }

    system("pause");
    return 0;
}

7-23两个有序序列的中位数（划分数组）

已知有两个非降序序列S1, S2, 求S1与S2归并成一个序列的低位中位数。有序序列A0,A1,⋯,AN−1的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数（A0为第1个数）。

输入格式：

输入分4行。第一行给出第一个序列的长度N1（0<N1≤2500000），随后是第一个序列的信息，即N1个非降序排列的整数。数字用空格间隔。随后是第二个序列的长度N2（0<N2≤2500000）和信息。因为测试数据只能10M，2.5*10的6次方规模，二分效果不明显，如果10的7次方数据规模，二分一般比归并快20ms左右。10的8次方快近200多ms。题目主要是输入花费大量的时间，如查找出现超时，尝试多次提交。

输出格式：

在一行中输出两个输入序列的并集序列的低位中位数。

输入样例：

3
1 2 3
5
4 5 6 7 8

输出样例：

4

思路：此题可以参考leetcode4.寻找两个正序数组的中位数官解方法二：

力扣

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, j, k, n, m;
    scanf("%d", &m);
    vector<int>nums1(m, 0);
    for (i = 0; i < m; ++i) {
        scanf("%d", &nums1[i]);
    }
    scanf("%d", &n);
    vector<int>nums2(n, 0);
    for (i = 0; i < n; ++i) {
        scanf("%d", &nums2[i]);
    }
    int median1 = 0, median2 = 0;
    if (nums1.size() > nums2.size()) {
        int m = nums2.size();
        int n = nums1.size();
        int left = 0, right = m;
        // median1：前一部分的最大值
        // median2：后一部分的最小值

        while (left <= right) {
            // 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
            // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
            int i = (left + right) / 2;
            int j = (m + n + 1) / 2 - i;

            // nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
            int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]);
            int nums_i = (i == m ? INT_MAX : nums1[i]);
            int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]);
            int nums_j = (j == n ? INT_MAX : nums2[j]);

            if (nums_im1 <= nums_j) {
                median1 = max(nums_im1, nums_jm1);
                median2 = min(nums_i, nums_j);
                left = i + 1;
            } else {
                right = i - 1;
            }
        }
    } else {
        int m = nums1.size();
        int n = nums2.size();
        int left = 0, right = m;
        // median1：前一部分的最大值
        // median2：后一部分的最小值

        while (left <= right) {
            // 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
            // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
            int i = (left + right) / 2;
            int j = (m + n + 1) / 2 - i;

            // nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
            int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]);
            int nums_i = (i == m ? INT_MAX : nums1[i]);
            int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]);
            int nums_j = (j == n ? INT_MAX : nums2[j]);

            if (nums_im1 <= nums_j) {
                median1 = max(nums_im1, nums_jm1);
                median2 = min(nums_i, nums_j);
                left = i + 1;
            } else {
                right = i - 1;
            }
        }
    }
    printf("%d", median1);

    system("pause");
    return 0;
}

7-24两个有序序列的中位数（二分）

已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A0,A1,⋯,AN−1的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数（A0为第1个数）。

输入格式：

输入分三行。第一行给出序列的公共长度N（0<N≤100000），随后每行输入一个序列的信息，即N个非降序排列的整数。数字用空格间隔。

输出格式：

在一行中输出两个输入序列的并集序列的中位数。

输入样例：

5
1 3 5 7 9
2 3 4 5 6

输出样例：

4

思路：插入并利用sort排序二分输出即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, n;
    cin >> n;
    vector<int>nums;
    for (i = 0; i < n * 2; i++) {
        int x;
        cin >> x;
        nums.push_back(x);
    }
    sort(nums.begin(), nums.end());
    cout << nums[(n * 2 - 1) / 2] << endl;

    system("pause");
    return 0;
}

7-25单身狗（模拟）

“单身狗”是中文对于单身人士的一种爱称。本题请你从上万人的大型派对中找出落单的客人，以便给予特殊关爱。

输入格式：

输入第一行给出一个正整数 N（≤50000），是已知夫妻/伴侣的对数；随后 N 行，每行给出一对夫妻/伴侣——为方便起见，每人对应一个 ID 号，为 5 位数字（从 00000 到 99999），ID 间以空格分隔；之后给出一个正整数 M（≤10000），为参加派对的总人数；随后一行给出这 M 位客人的 ID，以空格分隔。题目保证无人重婚或脚踩两条船。

输出格式：

首先第一行输出落单客人的总人数；随后第二行按 ID 递增顺序列出落单的客人。ID 间用 1 个空格分隔，行的首尾不得有多余空格。

输入样例：

3
11111 22222
33333 44444
55555 66666
7
55555 44444 10000 88888 22222 11111 23333

输出样例：

5
10000 23333 44444 55555 88888

思路：定义一个Map和一个Set容器，map用来存储一对夫妻的id，set存储需要查询的人的id，遍历需要查询的人，如果查询的人当中有人的编号能在map中找到，且这个人的另一半也能在set中能找到，则这个人不是单身狗，否则就加入结果数组中，最后排序格式化输出即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, j, k, n, m;
    cin >> n;
    map<int, int>mp1; 
    set<int>st;
    vector<int>res;
    for (i = 0; i < n; i++) {
        int a, b;
        cin >> a >> b;
        mp1[a] = b;
        mp1[b] = a;
    }
    cin >> m;
    vector<int>nums(m, 0);
    for (i = 0; i < m; i++) {
        cin >> nums[i];
        st.insert(nums[i]);
    }
    for (i = 0; i < m; i++) {
        if (mp1.find(nums[i]) == mp1.end() || st.find(mp1[nums[i]]) == st.end()) {
            res.push_back(nums[i]);
        }
    }
    sort(res.begin(), res.end());
    cout << res.size() << endl;
    for (i = 0; i < res.size(); i++) {
        if (i == 0)
            printf("%05d", res[i]);
        else
            printf(" %05d", res[i]);
    }


    system("pause");
    return 0;
}

7-26悄悄关注（模拟）

新浪微博上有个“悄悄关注”，一个用户悄悄关注的人，不出现在这个用户的关注列表上，但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探，根据某人的关注列表和其对其他用户的点赞情况，扒出有可能被其悄悄关注的人。

输入格式：

输入首先在第一行给出某用户的关注列表，格式如下：

人数N 用户1 用户2 …… 用户N

其中N是不超过5000的正整数，每个用户i（i=1, ..., N）是被其关注的用户的ID，是长度为4位的由数字和英文字母组成的字符串，各项间以空格分隔。

之后给出该用户点赞的信息：首先给出一个不超过10000的正整数M，随后M行，每行给出一个被其点赞的用户ID和对该用户的点赞次数（不超过1000），以空格分隔。注意：用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户，在点赞信息中也没有重复用户。

输出格式：

我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人，很可能是其悄悄关注的人。根据这个假设，请你按用户ID字母序的升序输出可能是其悄悄关注的人，每行1个ID。如果其实并没有这样的人，则输出“Bing Mei You”。

输入样例1：

10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60

输出样例1：

Ammy
Cath
Pota

输入样例2：

11 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao Pota
7
Magi 50
Pota 30
LLao 48
Ammy 3
Dave 15
GAO3 31
Zoro 29

输出样例2：

Bing Mei You

思路：简单模拟，直接上代码了

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i, j, k, n, m;
    double ave = 0;
    cin >> n;
    set<string>st;
    for (i = 0; i < n; i++) {
        string s;
        cin >> s;
        st.insert(s);
    }
    cin >> m;
    vector<pair<string, int>>nums(m);
    vector<string>res;
    for (i = 0; i < m; i++) {
        cin >> nums[i].first >> nums[i].second;
        ave += nums[i].second;
    }
    ave = ave * 1.0 / m;
    for (i = 0; i < m; i++) {
        if (nums[i].second > ave && st.find(nums[i].first) == st.end()) {
            res.push_back(nums[i].first);
        }
    }
    if (res.size() == 0) {
        cout << "Bing Mei You" << endl;
        return 0;
    }
    sort(res.begin(), res.end());
    for (i = 0; i < res.size(); i++) {
        cout << res[i] << endl;
    }

    system("pause");
    return 0;
}

7-27冰岛人（模拟+二叉树）

2018年世界杯，冰岛队因1:1平了强大的阿根廷队而一战成名。好事者发现冰岛人的名字后面似乎都有个“松”（son），于是有网友科普如下：

冰岛人沿用的是维京人古老的父系姓制，孩子的姓等于父亲的名加后缀，如果是儿子就加 sson，女儿则加 sdottir。因为冰岛人口较少，为避免近亲繁衍，本地人交往前先用个 App 查一下两人祖宗若干代有无联系。本题就请你实现这个 App 的功能。

输入格式：

输入首先在第一行给出一个正整数 N（1<N≤105），为当地人口数。随后 N 行，每行给出一个人名，格式为：名姓（带性别后缀），两个字符串均由不超过 20 个小写的英文字母组成。维京人后裔是可以通过姓的后缀判断其性别的，其他人则是在姓的后面加 m 表示男性、f 表示女性。题目保证给出的每个维京家族的起源人都是男性。

随后一行给出正整数 M，为查询数量。随后 M 行，每行给出一对人名，格式为：名1 姓1 名2 姓2。注意：这里的姓是不带后缀的。四个字符串均由不超过 20 个小写的英文字母组成。

题目保证不存在两个人是同名的。

输出格式：

对每一个查询，根据结果在一行内显示以下信息：

若两人为异性，且五代以内无公共祖先，则输出 Yes；
若两人为异性，但五代以内（不包括第五代）有公共祖先，则输出 No；
若两人为同性，则输出 Whatever；
若有一人不在名单内，则输出 NA。

所谓“五代以内无公共祖先”是指两人的公共祖先（如果存在的话）必须比任何一方的曾祖父辈分高。

输入样例：

15
chris smithm
adam smithm
bob adamsson
jack chrissson
bill chrissson
mike jacksson
steve billsson
tim mikesson
april mikesdottir
eric stevesson
tracy timsdottir
james ericsson
patrick jacksson
robin patricksson
will robinsson
6
tracy tim james eric
will robin tracy tim
april mike steve bill
bob adam eric steve
tracy tim tracy tim
x man april mikes

输出样例：

Yes
No
No
Whatever
Whatever
NA

思路：详见代码及注释（灵活运用STL），这里需要注意一下的是五代以内的定义，相同的话，一方必须要比另一方曾祖父辈分高，说通俗点就是：共同祖先是A的爸爸，是B的十几代祖宗，这样还是不可以的，因为在A的五代以内；或者B直接是A的直系亲属也有可能，样例图解如下

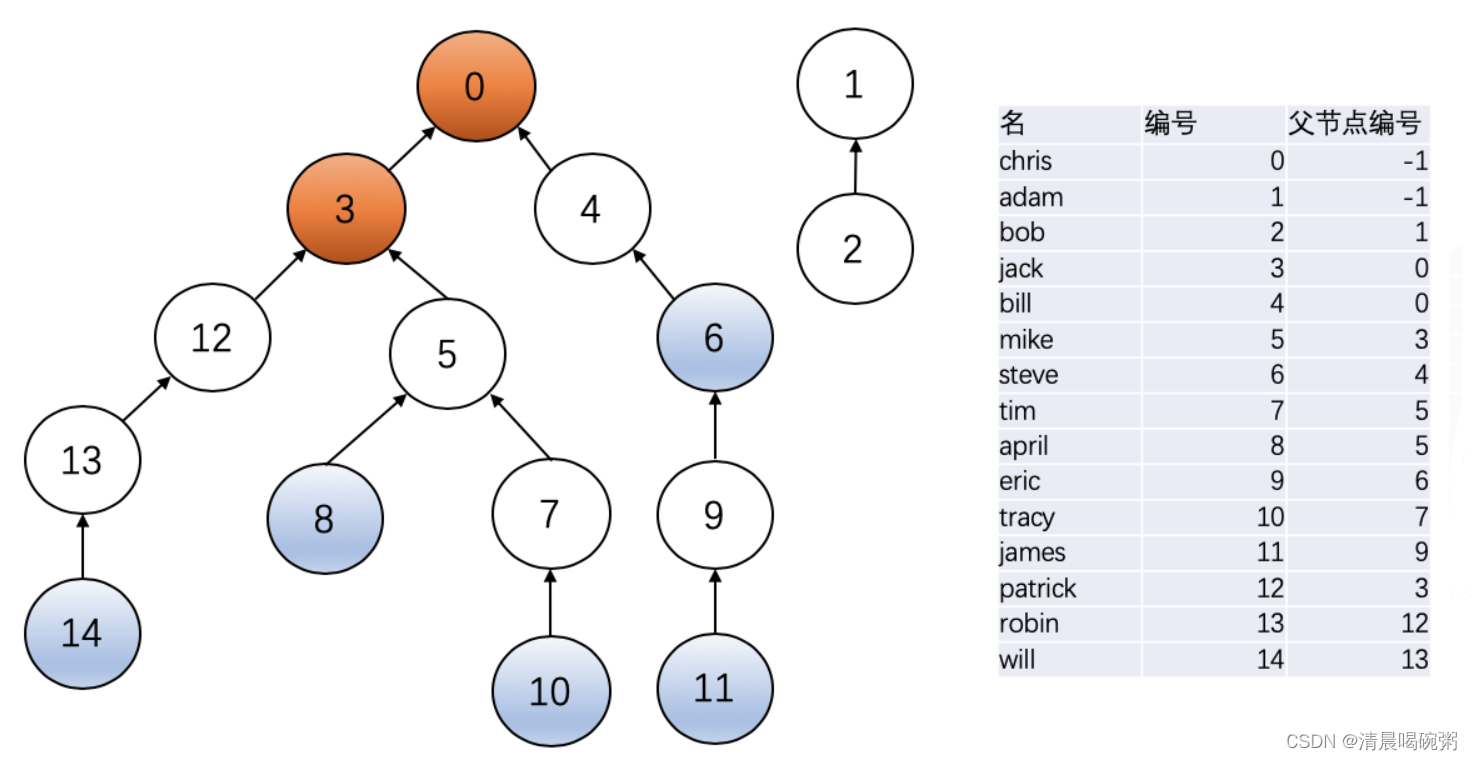
图解参考链接：

L2-030 冰岛人（25 分)_玩遍每座城的博客-CSDN博客

AC代码：

#include<bits/stdc++.h>
using namespace std;
//number给人名进行编号,sex存储性别,1是男性，2是女性
map<string, int>number, sex;
//建立二叉树
map<int, pair<int, int>>mp;
//寻找祖先函数
string check(vector<int> &parent, int a, int b) {
    int item = a;
    int cnt1 = 1, cnt2 = 1;
    map<int, int>nums;
    while (item != INT_MIN) {
        if (item == b)
            return "No";
        nums[item] = cnt1;
        item = parent[item];
        cnt1++;
    }
    item = b;
    while (item != INT_MIN) {
        if (nums.find(item) != nums.end() ) {
            if (cnt2 >= 5 && nums[item] >= 5)
                return "Yes";
            else if (cnt2 < 5 || nums[item] < 5)
                return "No";
        }
        item = parent[item];
        cnt2++;
    }
    return "Yes";
}
int main()
{
    int i, j, k, n, m;
    cin >> n;
    vector<pair<string, string>>nums(n);
    //存储每个孩子节点的父节点
    vector<int>parent(n, 0);    
    for (i = 0; i < n; i++) {
        cin >> nums[i].first >> nums[i].second;
        number[nums[i].first] = i; //对每个人进行编号
        mp[i].first = mp[i].second = INT_MIN;
    }
    for (i = 0; i < n; i++) {
        int len = nums[i].second.length();
        string temp = "";
        //存储性别以及每个孩子的父节点,没父节点赋值为INT_MIN，有则为其编号
        if (nums[i].second[len - 1] == 'm' || nums[i].second[len - 1] == 'f') {
            sex[nums[i].first] = nums[i].second[len - 1] == 'm' ? 1 : 0;            
        } else if (nums[i].second[len - 1] == 'n') {
            sex[nums[i].first] = 1;
            temp = nums[i].second.substr(0, len - 4);
        } else if (nums[i].second[len - 1] == 'r') {
            sex[nums[i].first] = 0;
            temp = nums[i].second.substr(0, len - 7);
        }
        parent[i] = number.find(temp) == number.end() ? INT_MIN : number[temp];
        //建树
        if (parent[i] != INT_MIN && mp[parent[i]].first == INT_MIN)
            mp[parent[i]].first = i;
        else 
            mp[parent[i]].second = i;
    }
    cin >> m;
    string surname1, surname2, name1, name2;
    vector<string>res;
    for (i = 0; i < m; i++) {
        cin >> name1 >> surname1 >> name2 >> surname2;
        if (number.find(name1) == number.end() || number.find(name2) == number.end()) {
            res.push_back("NA");
            continue;
        }
        if (sex[name1] == sex[name2]) {
            res.push_back("Whatever");
            continue;
        }
        res.push_back(check(parent, number[name1], number[name2]));
    }
    for (i = 0; i < res.size(); i++) {
        cout << res[i] << endl;
    }

    system("pause");
    return 0;
}