Machine Learning Park --聚类

5 聚类（Clustering）

本文Github仓库已经同步文章与代码https://github.com/Gary-code/Machine-Learning-Park/tree/main/Part1%20Machine%20Learning%20Basics

代码说明：

文件名	说明
k_means.ipynb	从0开始实现k-Means
GMM.ipynb	GMM从零开始实现
k_means_practice.ipynb	K_Means算法解决文本词汇聚类
corpus_train.txt	用于K_Means聚类的文本数据集

如果你有时刻留意我们项目在github上的地址，你或许会发现从这里开始的代码会逐渐偏重于理论探讨和场景应用。主要为了更好的将我们所讲的理论知识用于实践当中。

由于当前处于基础知识讲解版块，我们尽量控制为简单的实践。真正工业级别的实践，我们将在项目第二版块（当下应用）陆续为大家揭晓更多内容，敬请期待🚀

有错误欢迎读者联系我指正。

与前面讲解的算法模型不一样，聚类是一种无监督学习(Unsupervised Learning)的方式。

5.1 无监督学习

与有监督学习最大的不同，就是学习的数据是没有标签的。

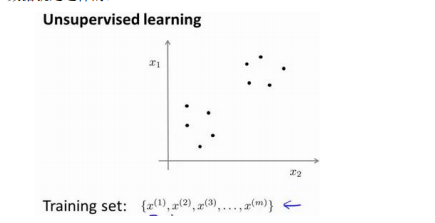
在无监督学习的过程当中，我们需要输入一些没有标签的数据，让算法帮我们找到数据内在结构。对于聚类问题而言，这种内在结构就是类别。

上图的数据看起来可以分开成为两个点集（簇），一个能够找到这两个簇的算法，就是我们这里要说的聚类算法。

这里我们将介绍两个聚类算法：

• K-Means（K均值）
• GMM（高斯混合模型）

5.2 K-Means

K-Means算法步骤非常简单，具体过程为下面：

• 首先选择𝐾个随机的点，称为聚类中心（cluster centroids）；
• 对于数据集中的每一个数据，按照距离𝐾个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。
• 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。
• 重复步骤，直至中心点几乎不再变化。

伪代码：

Repeat {
    for i = 1 to m
    c(i) := index (form 1 to K) of cluster centroid closest to x(i)
    for k = 1 to K
    μk := average (mean) of points assigned to cluster k
}

优化目标和损失函数

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：
$$J\left(c^{(1)},\dots ,c^{(m)},{\mu }_1,\dots ,{\mu }_K\right)=\frac{1}{m}\sum _{i=1}^m{\Vert X^{(i)}-{\mu }_{c^{(i)}}\Vert }^2$$
其中Font metrics not found for font: .代表与$x^{(i)}$最近的聚类中心点。

对此我们可以分析出：

• 第一个循环是用于减小$c^{(i)}$引起的代价
• 而第二个循环则是用于减小Font metrics not found for font: .引起的代价。
• 迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误。

初始化问题

由于我们开始选取的K个点是随机的，因此算法有可能会停留在一个局部最小值处。

为了解决这个问题，我们通常需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果。

聚类数量选择

另外一个可调节的参数就是K，聚类的数量。我们通常采用“肘部法则”来决定。如果你接触过主成分析法(PCA)，肯定对此不会感到陌生。

所有的数据都会分到一个聚类里，然后计算成本函数或者计算畸变函数$J$。$K$代表聚类数量。

下面我们来看一个例子：

通过分析，使用3个类别来进行聚类是正确的。

5.3 GMM（高斯混合模型）

与K均值算法类似，同样使用了EM算法进行迭代计算。

高斯混合模型假设每个簇的数据都是符合高斯分布（正态分布），因此当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。

高斯混合模型的核心思想是，假设数据可以看作从多个高斯分布中生成出来的。

在该假设下，每个单独的分模型都是标准高斯模型:

• 其均值 ${\mu }_k$ 和方差 ${\sigma }_k$ 是待估计的参数
• 每个分模型都还有一个参数 ${\alpha }_k$
• 参数表示为${\theta }_k$可以理解为权重或生成数据的概率。高斯混合模型的公式为：

$$P(x\mid \theta )=\sum _{k=1}^K{\alpha }_k\varphi \left(x\mid {\theta }_k\right)$$

对于上面三个参数的求解，我们开始的想法或许是采用概率统计学当中的最大似然估计的方法。遗憾的是，此问题中直接使用最大似然估计，得到的是一 个复杂的非凸函数，目标函数是和的对数，难以展开和对其求偏导，其表达式如下：
$$\log L(\theta )=\sum _{j=1}^N\log P\left(x_j\mid \theta \right)=\sum _{j=1}^N\log \left(\sum _{k=1}^K{\alpha }_k\varphi \left(x\mid {\theta }_k\right)\right)$$

这种情况下可以采用EM算法来求解。

EM算法

1. E-step：求期望 $E\left({\gamma }_{jk}\mid X,\theta \right)$ for all $j=1,2,...N;k=1,2,...,K$。
2. M-step：求极大，计算新一轮迭代的模型参数。

EM算法是在最大化目标函数时：

1. 固定一个变量使整体函数变为凸优化函数。
2. 求导得到最值。
3. 利用最优参数更新被固定的变量，进入下一个循环。

对于GMM：

首先，随机初始化参数的值。然后，重复下述两步，直到收敛。

• E步骤。依据当前参数，计算每个数据$j$来自子模型$k$的可能性。

$${\gamma }_{jk}=\frac{{\alpha }_k\varphi \left(x_j\mid {\theta }_k\right)}{{\sum }_{k=1}^K{\alpha }_k\varphi \left(x_j\mid {\theta }_k\right)},j=1,2,\dots ,N;k=1,2,\dots ,K$$

• M步骤。使用E步骤估计出的概率，来改进每个分模型的均值，方差和权重。如下所示，注意：每计算完一个值就马上更新！

$${\mu }_k=\frac{{\sum }_j^N\left({\gamma }_{jk}{x}_j\right)}{{\sum }_j^N{\gamma }_{jk}},k=1,2,\dots ,K$$

用这一轮更新后的${\mu }_k$：
$${\sigma }_k=\frac{{\sum }_j^N{\gamma }_{jk}\left(x_j-{\mu }_k\right){\left(x_j-{\mu }_k\right)}^T}{{\sum }_j^N{\gamma }_{jk}},k=1,2,\dots ,K$$

$${\alpha }_k=\frac{{\sum }_{j=1}^N{\gamma }_{jk}}{N},k=1,2,\dots ,K$$
重复E-M过程，直到收敛。

举一个例子：

高斯混合模型是一个生成式模型。可以这样理解数据的生成过程，假设一个最简单的情况，即只有两个一维标准高斯分布的分模型N(0,1)和N(5,1)，其权重分别为0.7和0.3。

那么，在生成第一个数据点时，先按照权重的比例，随机选择一个分布，比如选择第一个高斯分布，接着从N(0,1)中生成一个点，如−0.5，便是第一个数据点。

在生成第二个数据点时，随机选择到第二个高斯分布N(5,1)，生成了第二个点4.7。如此循环执行，便生成出了所有的数据点。

也就是说，我们并不知道最佳的K个高斯分布的各自3个参数，也不知道每个数据点究竟是哪个高斯分布生成的。所以每次循环时：

• 先固定当前的高斯分布不变，获得每个数据点由各个高斯分布生成的概率。
• 然后固定该生成概率不变，根据数据点和生成概率，获得一个组更佳的高斯分布。
• 循环往复，直到参数的不再变化，或者变化非常小时，便得到了比较合理的一组高斯分布。

与K-Means相比，GMM同样需要指定K类别，且都往往只能收敛于局部最优。

但其有点就是，引入了概率的知识：

• 可以给出一个样本属于某类的概率是多少。
• 不仅仅可以用于聚类，还可以用于概率密度的估计。
• 并且可以用于生成新的样本点。

5.4 参考资料