MST(minimum spanning tree)即最小生成树算法,经典的有两个,这里介绍一下kruskal算法。关于另外的一个prim算法,本blog也将介绍。
何谓最小生成树呢?大家知道树就是每个结点可以相互到达,并且没有环的一种数据结构,这里就不多介绍了,何谓最小生成树呢?就是从一个图中选取若干条边,这些边使得每个结点之间可以相互到达,最关键就是,选取的这些边的权值之和是最小的。
下面看一个图
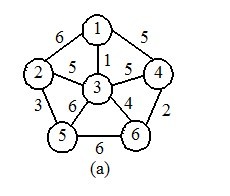
那么这个图的最小生成树就是
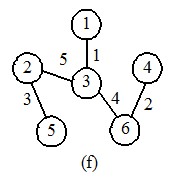
下面我们介绍一下kruskal算法的基本思想,然后再对照算法看看上面那棵最小生成树是如何生成的
1.从图中选取权值最小的一条边将权值加到sum中(sum记录最小生成树的边的总权值)
2.继续图里面选取权值次小的边加到sum,但是以后继续选边有个条件,即所选的边与前面选的边不能构成环(因为这是求最小生成树嘛)
3.重复2步骤直到选了|V|-1条边(V代表图的结点总数),为什么呢?因为一棵树的的边数比结点数少1嘛
这里的关键是如何判断它是否有环(建议读者去看看本blog的对于并查集的讲解,或者去看别人的(呵呵))
这里简单举个例子介绍一下比如说图a中,我们先选了3-6这条边,于是设置parent[6]=3,然后又选4-6这条边
因为6的父亲是3,比4小,于是我们设置parent[4]=3,假设我们要选3-4这条边,由于初始化父亲的时候设置的parent[3]=3本身,这个时候我们发现parent[3]=3,parent[4]也等于3,于是断定这构成了环(很巧妙吧。),当然这只是简单介绍,建议没学过并查集的读者,先去看看并查集再看本blog。
好了,算法的基本思想就是这样,其实就是贪心嘛,现在我们看看上图的最小生成树是如何生成的


1.先对边进行排序(sort函数很快嘛。)
2.选1-3这条边,再选4-6这条边,再选2-5这条边,再选3-6这条边,再选1-4或者2-3,选1-4的时候,我们发现构成了环(1-3-6-4-1),于是不选他,选2-3。最终选了6-1=5条边。
推荐题目
http://acm.hdu.edu.cn/showproblem.php?pid=1863
何谓最小生成树呢?大家知道树就是每个结点可以相互到达,并且没有环的一种数据结构,这里就不多介绍了,何谓最小生成树呢?就是从一个图中选取若干条边,这些边使得每个结点之间可以相互到达,最关键就是,选取的这些边的权值之和是最小的。
下面看一个图

那么这个图的最小生成树就是

下面我们介绍一下kruskal算法的基本思想,然后再对照算法看看上面那棵最小生成树是如何生成的
1.从图中选取权值最小的一条边将权值加到sum中(sum记录最小生成树的边的总权值)
2.继续图里面选取权值次小的边加到sum,但是以后继续选边有个条件,即所选的边与前面选的边不能构成环(因为这是求最小生成树嘛)
3.重复2步骤直到选了|V|-1条边(V代表图的结点总数),为什么呢?因为一棵树的的边数比结点数少1嘛
这里的关键是如何判断它是否有环(建议读者去看看本blog的对于并查集的讲解,或者去看别人的(呵呵))
这里简单举个例子介绍一下比如说图a中,我们先选了3-6这条边,于是设置parent[6]=3,然后又选4-6这条边
因为6的父亲是3,比4小,于是我们设置parent[4]=3,假设我们要选3-4这条边,由于初始化父亲的时候设置的parent[3]=3本身,这个时候我们发现parent[3]=3,parent[4]也等于3,于是断定这构成了环(很巧妙吧。),当然这只是简单介绍,建议没学过并查集的读者,先去看看并查集再看本blog。
好了,算法的基本思想就是这样,其实就是贪心嘛,现在我们看看上图的最小生成树是如何生成的


1.先对边进行排序(sort函数很快嘛。)
2.选1-3这条边,再选4-6这条边,再选2-5这条边,再选3-6这条边,再选1-4或者2-3,选1-4的时候,我们发现构成了环(1-3-6-4-1),于是不选他,选2-3。最终选了6-1=5条边。
最后贴下模板
#include <iostream>
#include <cstdlib>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
int parent[101];
struct Edge
{
int u,v;
int len;
};
struct Graph
{
int vexnum;
int vecnum;
Edge edge[10001];
}G;
bool cmp(Edge a,Edge b)
{
return a.len<b.len;
}
void Unitparent(Graph G)
{
int i;
for(i=1;i<=G.vexnum;i++)
parent[i] = i;
}
int Find(int x)
{
int i=x,tem;
while(i!=parent[i])//找到祖先
i = parent[i];
while(i!=x)//非递归压缩路径
{
tem = parent[x];
parent[x] = i;
x = tem;
}
return i;
}
void Unionset(int x,int y)
{
int x1 = Find(x),y1 = Find(y);
if(x1>y1) parent[x] = y1;
else parent[y] = x1;
}
int kruskal(Graph G)
{
int i;
int sum_weight = 0;
int num = 0;//已选边的数目
sort(G.edge,G.edge+G.vecnum,cmp);
Unitparent(G);//初始化所有顶点的祖先
for(i=0;i<G.vecnum;i++)
{
if(Find(G.edge[i].u)!=Find(G.edge[i].v))//没有构成环
{
sum_weight += G.edge[i].len;
num++;//所选边数+1
Unionset(G.edge[i].u,G.edge[i].v);//并查集的合并操作
if(num>=G.vexnum-1) break;
}
}
if(num<G.vexnum-1) return 0;//算选的边数比结点数-1小,此图肯定不是连通图咯,最小生成树不存在。
return sum_weight;
}推荐题目
http://acm.hdu.edu.cn/showproblem.php?pid=1863






















 817
817

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








