[蓝桥杯 2025 省研究生组] 01 串

P12191 [蓝桥杯 2025 省研究生组] 01 串

题目链接

[蓝桥杯 2025 省研究生组] 01 串

题目描述

给定一个由 $0,1,2,3\dots$ 的二进制表示拼接而成的长度无限的 $01$ 串。其前若干位形如 $011011100101110111\dots$。

请求出这个串的前 $x$ 位里有多少个 $1$。

输入格式

输入的第一行包含一个正整数 $x$。

输出格式

输出一行包含一个整数表示答案。

输入输出样例 #1

输入 #1

7

输出 #1

5

说明/提示

样例说明

给定的串的前 $7$ 位为 $0110111$。

评测用例规模与约定

• 对于 $60\%$ 的评测用例，$x\le 10^6$；
• 对于所有评测用例，$1\le x\le 10^{18}$。

解题思路

如果我们能够知道完整的数字有多少个，就很容易能够求出二进制中有多少个1。比如完整的数字有28个（但其实最大是27），$0$到$27$的二进制如下：

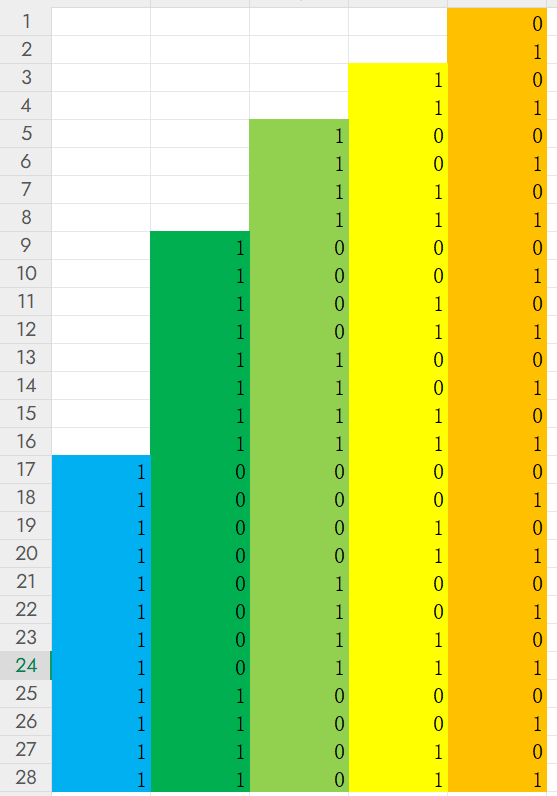
我们可以轻松得出第$i$位有多少个1，可以通过如下公式计算：
$num{s}_1[i]=\lfloor n/2^i\rfloor \ast 2^{i-1}+(n\%2^i)-2^{i-1}+1$
根据图，可以分析出$1$的分布规律，再稍微推导一下就能得出这个公式。
对于不完整的数字（肯定只会有一个不完整的数字，不完整的数字肯定是最大的完整的数字加1），只需要知道剩余多少位，就能很轻松计算出$1$的个数。剩余多少位，只需要减去前面$i-1$位总的位数，再对$i$取余即可。

怎么知道完整的数字有多少个呢？对于这样非常长的串，基本思路肯定是分块。那么怎样分块呢？第一想法是按照数字，一个数字分为一块，但是因为$1\le x\le 10^{18}$，粗略估计一下，数字最大大约为为$2^{55}$，就需要分为$2^{55}$块，远远超过了$10^8$，明显是不行的。再考虑一下按照二进制的位数，将二进制位数相同的数字分到一块中，这样的就只需要分成55块了。
思路其实很简单，具体实现可以看以下代码。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll nums1[64];//nums1[i]表示从 0-（2^i）-1的01串中有nums1[i]个1
ll nums[64];//nums[i]表示从 0-（2^i）-1的01串共有nums[i]位
ll pows_2[64];//在计算过程中会多次用到2的次方，为了提高速度，用一个数组来记录
ll x;

ll get_1_nums(ll xx) {
	ll res = 0;
	//求出最大的完整的数字的二进制位数
	int i = 0;
	while (1) {
		if (nums[i] == xx)
			return nums1[i];//如果刚好等与nums[i]，1的个数为nums1[i]
		if (nums[i] > xx)
			break;
		++i;
	}
	ll rest = (xx - nums[i - 1]) / i;//(xx - nums[i - 1])表示2^（i-1）-1之后剩下多少位，
									//而i是当前数字的位数，(xx - nums[i - 1]) / i就表示完整的数有多少个
	ll n = pows_2[i - 1] + rest - 1;//n表示最大的完整的数，因为nums[i - 1]表示的是0-2^（i-1）-1，而pows_2[i - 1]是0-2^（i-1），相差一，所以需要减去
	//计算每一位总共有多少1
	int ii = 1;
	while (ii <= i) {
		res += (n / pows_2[ii]) * pows_2[ii - 1];
		if (n % pows_2[ii] >= pows_2[ii - 1])
			res += (n % pows_2[ii]) - pows_2[ii - 1] + 1;
		ii++;
	}
	//y表示不完整的数，即n+1
	ll y = n + 1;
	//rest_bit剩下还有多少位
	ll rest_bit = (xx - nums[i - 1]) % i;
	//从高位开始计数并计算
	i = i - 1;
	while (rest_bit--) {
		if (y >= pows_2[i])
		{
			res++;
			y -= pows_2[i];
		}
		i--;
	}
	return res;
}
int main() {
	pows_2[0] = 1;
	for (int i = 1;i < 64;++i)
		pows_2[i] = pows_2[i - 1] * 2;
	int idx = 1;//idx表示有数位
	nums[0] = 1;//这里方便处理x为1时的情况
	nums[idx++] = 2;//把0也算到1位中
	cin >> x;
	while (1) {
		nums[idx] = nums[idx - 1] + idx * pows_2[idx - 1];//对于i位数，总共有2^(i-1)个
		if (nums[idx] > x)
			break;
		idx++;
	}
	nums1[1] = 1;
	for (int i = 2;i <= idx;++i)
		nums1[i] = 2 * nums1[i - 1] + pows_2[i - 1];//对于i位数，前面肯定是1（有2^(i-1)个），
													//后面的i-1位其实是重复前面的
	cout << get_1_nums(x);
	return 0;
}