Triangle War
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 1489 | Accepted: 595 |
Description
Triangle War is a two-player game played on the following triangular grid:
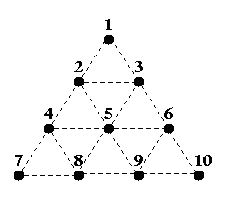
Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.
For example, if A fills in the line between 2 and 5 in the partial game on the left below:
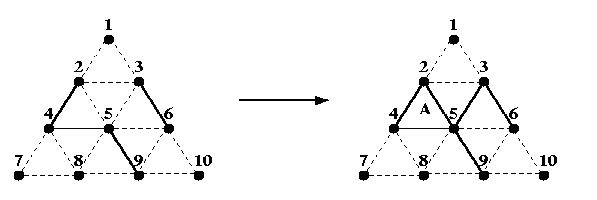
Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.

Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.
For example, if A fills in the line between 2 and 5 in the partial game on the left below:

Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.
Input
You will be given a number of games in the input. The first line of input is a positive integer indicating the number of games to follow. Each game starts with an integer 6 <= m <= 18 indicating the number of moves that have been made in the game. The next m lines indicate the moves made by the two players in order, each of the form i j (with i < j) indicating that the line between i and j is filled in that move. You may assume that all given moves are legal.
Output
For each game, print the game number and the result on one line as shown below. If A wins, print the sentence "A wins." If B wins, print "B wins."
Sample Input
4 6 2 4 4 5 5 9 3 6 2 5 3 5 7 2 4 4 5 5 9 3 6 2 5 3 5 7 8 6 1 2 2 3 1 3 2 4 2 5 4 5 10 1 2 2 5 3 6 5 8 4 7 6 10 2 4 4 5 4 8 7 8
Sample Output
Game 1: B wins. Game 2: A wins. Game 3: A wins. Game 4: B wins.
Source
解题思路:
总共有18条边,每条边只有两种状态:已填充或未填充,又,已知至少6个步骤,所以需要搜索的状态最多为2^12种;
为了表示状态,我们设计每条边占据一个bit位,这样2^18种状态都可以表示出来;
DP的重点在于递推式,我们假设state[i]表示某玩家在i状态下,填充某一条边得到的最大的三角形差值(自己获得的 - 对方玩家获得的),我们试遍每一条可以添加的边,假设可以添加边id,如果id添加后获得三角形(gTri(i, id) > 0),这时可以连续添加,获得三角形数nt = gTri(i, id) + state[i];否则nt = gTir(i, id) - state[i];试遍所有可以添加的边后,最大的nt作为state[i]的值记录下来。


























 326
326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








