[NOI2005] 月下柠檬树（自适应辛普森积分）

原创于 2021-08-17 20:55:08 发布 · 473 阅读

0 ·

CC 4.0 BY-SA版权

计算几何专栏收录该内容

4 篇文章

订阅专栏

本文讲解了如何通过分解柠檬树为圆台，利用自适应辛普森积分求解投影面积，重点提及了避免重复查找最大影子区域的优化技巧。算法涉及梯形与圆的交点计算和投影面积计算，提升效率的关键在于对称性和预处理边界信息。

题目

原题链接：点这里

总体思路–>问题转化

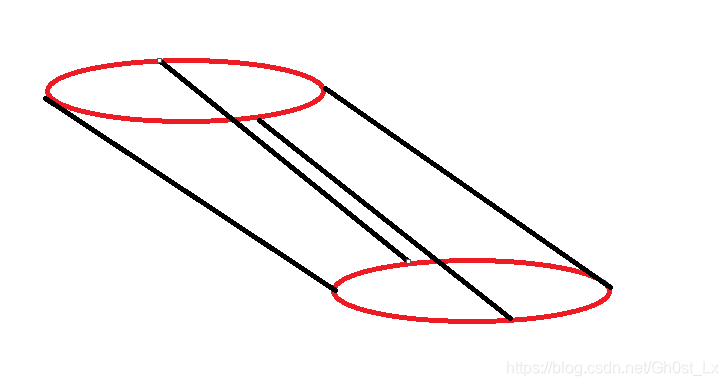
先将原本的柠檬树分解成为多个圆台，再单独看圆台的投影
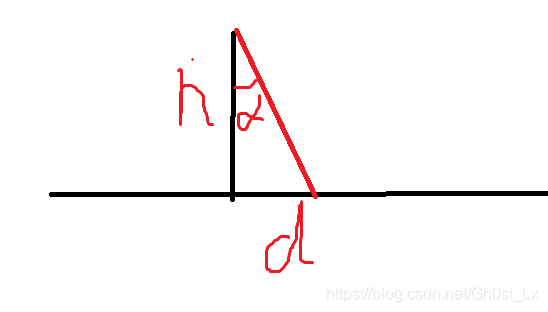
一个圆在地面的投影，是等比例的，而一条竖线的投影长度 $d=\cfrac{h}{\tan \alpha}$ ，这样也就得到了整棵树在平面上面的投影

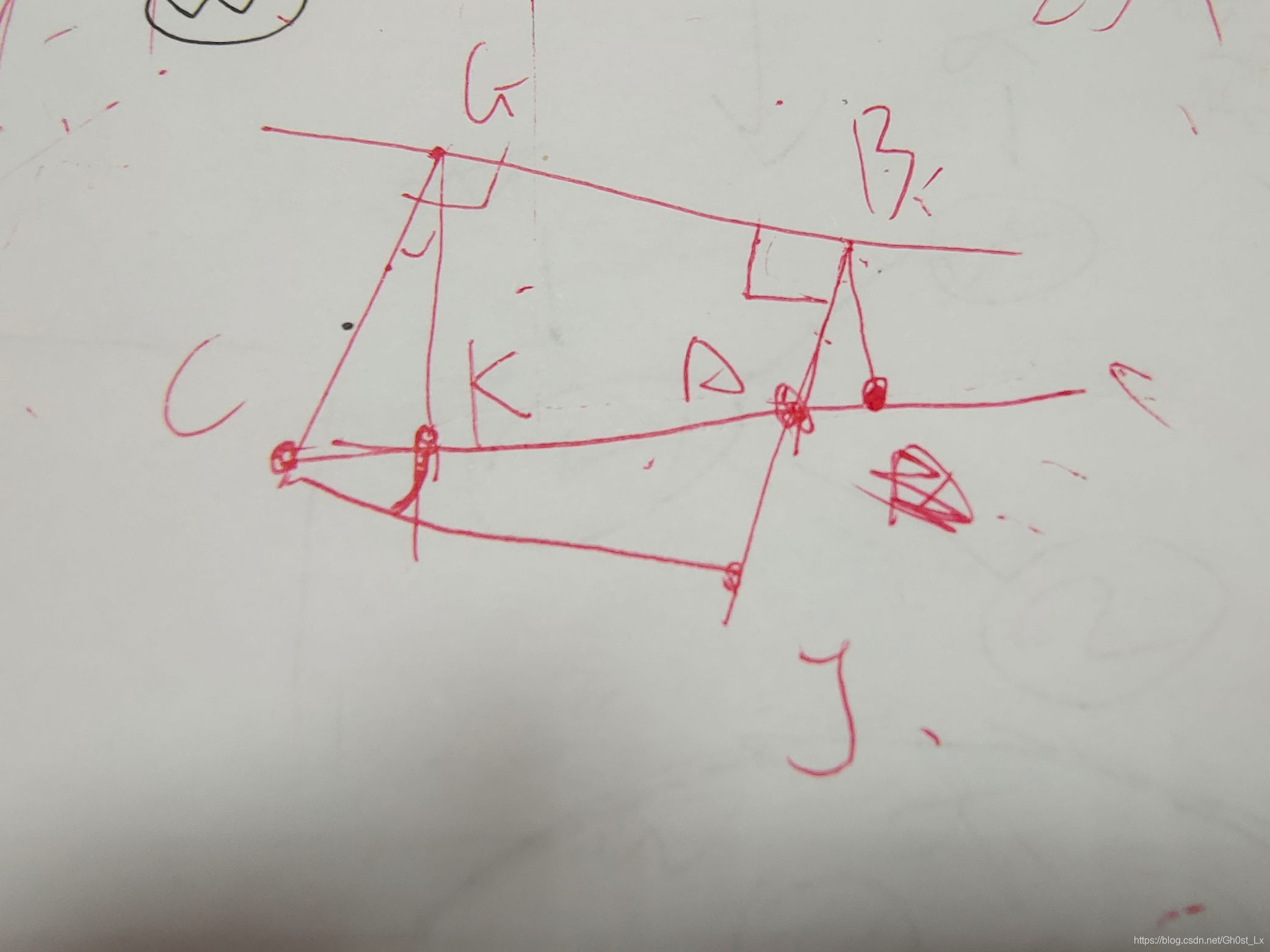
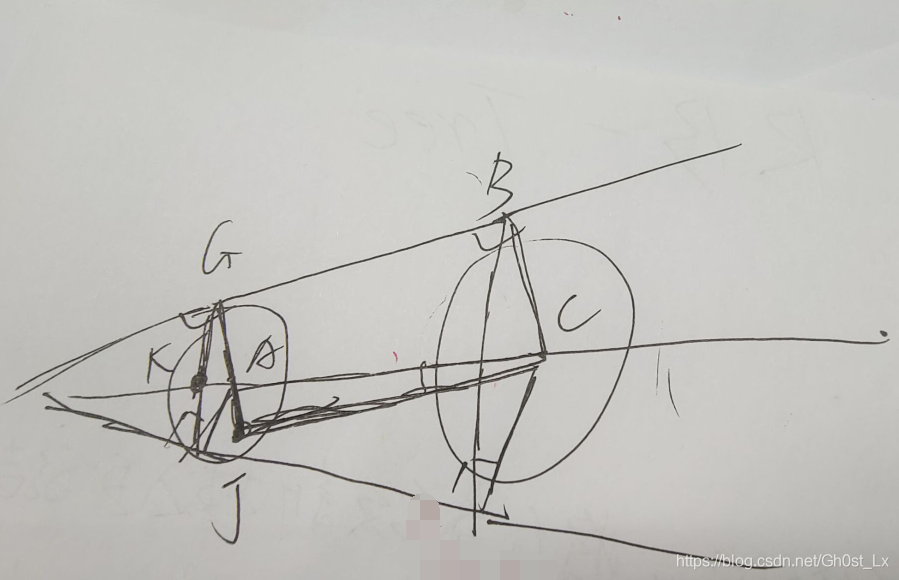
在这里插入图片描述

问题转换为面积并，显然自适应辛普森积分套上去就行了
还有一个易错的点，就是函数 $F (x)$ ，每次找的时候都要 $O (n)$ 找一遍最大值，因为大的影子可能会覆盖掉前后很多区间小的影子。
（PS：此处引用谷站的图，不过谷站的图忽略了我说的这种情况，我就在上面做了修改）

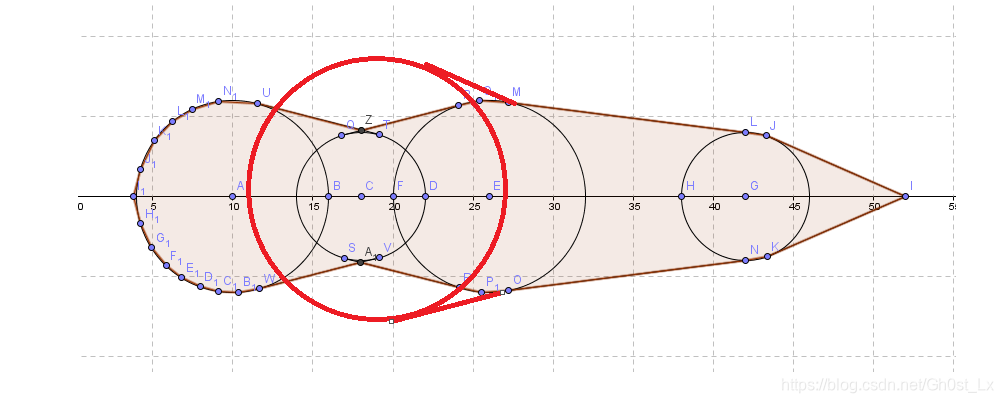
算法思路

由于影子关于 $x$ 轴对称，故我们只计算 $x$ 轴的直角梯形，最后 $a n s * 2$ 即可
然后我们需要快速计算出，对于 $x = X$ ，它和梯形和圆的交点的最大 $Y$ 是多少
所以我们需要预处理直角梯形的左右边界，斜边的斜率和截距
然后 $O (n)$ 跑一遍即可知道答案，此处不能找到就break，因为圆、梯形之间以及自身可能会有覆盖，所以要取max
解决了f(x)函数，剩下的自适应辛普森积分套进去就行了

代码实现

// #pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double

typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
typedef map<int, int> mii;
typedef mii::iterator mii_it;

const int N = 510, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;

int T, n, m;
db alpha, cot;

struct Circle
{
    db x, R;
} c[N]; //记录圆

struct qujian
{
    db l, r, k, b;
} sc[N]; //只记录梯形
//梯形和梯形之间还是有圆弧段的

int sign(db x)
{
    if (fabs(x) < eps)
        return 0;
    if (x < 0)
        return -1;
    return 1;
}

int dcmp(db x, db y)
{
    if (fabs(x - y) < eps)
        return 0;
    if (x < y)
        return -1;
    return 1;
}

db calc(db c, db a)
{
    return sqrt(c * c - a * a);
}

void get_k_b(int a, int b) //圆x和圆y之间的梯形
{
    int cmp = dcmp(c[a].R, c[b].R);
    if (cmp == 0) //两个圆半径相等
    {
        sc[a].l = c[a].x;
        sc[a].r = c[b].x;
        sc[a].k = 0;
        sc[a].b = c[a].R;
        return;
    }
    db AC = c[b].x - c[a].x, AJ = fabs(c[a].R - c[b].R); //如图
    db ly, ry;                                           //梯形的上底，下底
    if (cmp == 1)
    {
        sc[a].l = c[a].x + c[a].R * AJ / AC; //梯形左端
        sc[a].r = c[b].x + c[b].R * AJ / AC; //梯形右端
        ly = calc(c[a].R, sc[a].l - c[a].x);
        ry = calc(c[b].R, sc[a].r - c[b].x);
    }
    else
    {
        sc[a].l = c[a].x - c[a].R * AJ / AC;
        sc[a].r = c[b].x - c[b].R * AJ / AC;
        ly = calc(c[a].R, c[a].x - sc[a].l);
        ry = calc(c[b].R, c[b].x - sc[a].r);
    }
    sc[a].k = (ly - ry) / (sc[a].l - sc[a].r); //联立方程求解k,b
    sc[a].b = ly - sc[a].k * sc[a].l;
    return;
}

db f(db x)
{
    db ans = 0;
    loop(i, 0, n)
    {
        //x在圆内，因为梯形之间有圆弧段
        //dcmp==0的情况没必要计算，圆上一点的长度为0
        if (dcmp(x, c[i].x - c[i].R) > 0 && dcmp(x, c[i].x + c[i].R) < 0)
            ans = max(ans, calc(c[i].R, c[i].x - x));
        //x在梯形内
        if (dcmp(x, sc[i].l) >= 0 && dcmp(x, sc[i].r) <= 0)
            ans = max(ans, sc[i].k * x + sc[i].b); //y = kx+b
    }
    return ans;
}

db simpson(db l, db r)
{
    auto mid = (l + r) / 2;
    return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}

db asr(db l, db r, db s)
{

    auto mid = (l + r) / 2;
    db left = simpson(l, mid), right = simpson(mid, r);
    if (!dcmp(left + right, s))
        return left + right; //left和right分的更细，进度更高
    else
        return asr(l, mid, left) + asr(mid, r, right); //继续自适应
}

int main()
{
    cin.tie(0);
    cout.tie(0);
    cin >> n >> alpha;
    cot = 1.0 / tan(alpha); //求解出cot，接下来也只会用到cot
    cin >> c[0].x;
    c[0].x *= cot;
    rep(i, 1, n)
    {
        cin >> c[i].x;
        c[i].x = c[i].x * cot + c[i - 1].x;
    }
    loop(i, 0, n)
            cin >>
        c[i].R;
    c[n].R = 0; //树顶是一个顶点，为圆锥
    rep(i, 0, n - 1)
        get_k_b(i, i + 1);
    db L = c[0].x - c[0].R, R = c[n].x; //影最左边，和影子最右边
    loop(i, 0, n)
    {
        L = min(c[i].x - c[i].R, L); //因为要考虑某个圆的影子特别大的情况
        R = max(c[i].x + c[i].R, R);
    }
    printf("%.2lf\n", 2.0 * asr(L, R, simpson(L, R)));
    //我们只计算了x轴上方的，故要乘以2
    return 0;
}