简明理解：微积分基本定理

AI 时代学什么，怎么学 / 2024.12

怀疑一切和相信一切是两种同等方便的办法，因为两者都无须思考。

——亨利·庞加莱（1854—1912）

---

文章来自：公众号数科动力

微积分是微分学和积分学的统称，它的萌芽、发生与发展是一个跨文明、跨时代的累积过程，大体可以分为三个阶段：极限概念；求积的无限小方法；积分与微分的互逆关系 。前两阶段的工作，可以从欧洲的大批数学家一直追朔到古希腊的阿基米德的贡献（具体细节可以查看微积分发展 |（学法合集）参照前美国数学协会会长的建议）。最后一步则是由牛顿、莱布尼兹各自独立完成的。

若论对现代微积分的影响，莱布尼茨的成果可能更为深刻：

1 莱布尼茨发现，计算面积和变化率的问题从某种意义上说很有代表性，因为许多不同种类的问题都可以还原为这两类问题中的某一类。

2 他认识到，求解这两类问题的数学运算实际上彼此互为逆运算。今天，这些运算分别被称为积分和微分，它们彼此相反的这个事实就是人们所熟知的“微积分基本定理”。

3 莱布尼茨为这些运算发展出了一套恰当的符号（一直沿用至今），∫表示积分，d表示微分。他发现了实现微分和积分所需的数学规则。

（这三条论断引自第一推动丛书之《逻辑的引擎》）

由此便引出了本篇的主角——微积分基本定理。

微积分基本定理，也称为牛顿-莱布尼茨公式，是微积分学中的核心定理之一，它是联系导数、微分、不定积分、定积分的桥梁和纽带，联系了微分和积分这两个基本的数学运算。这个定理包含两个部分，通常称为第一基本定理和第二基本定理。

❝

微积分基本定理的第一部分（原函数的存在性，在《简明微积分》中称“微分形式”）:

如果函数（）在区间上连续，是内的某一固定点，令

则在上可微，并且

即

这个定理保证了对于任何连续函数，我们总能找到至少一个原函数。

微积分基本定理的第二部分（定积分的计算,在《简明微积分》中称“积分形式”）:

设在区间上可微，且等于连续函数，那么则有：

这个等式表明，我们可以使用原函数来计算定积分。

有了这个推论之后，求定积分的问题就可以转化为求原函数或不定积分的问题了。

微积分基本定理的几何意义

微积分基本定理的几何意义可以从原函数和定积分的角度来理解。

第一部分的几何意义:

原函数可以看作是从到区间内函数下的累积面积。随着在区间内变化，代表了从起点到任意点下方曲线与轴围成的面积。

由于是的一个原函数，意味着在某一点的瞬时变化率（即导数）正好等于在那一点的函数值。换句话说，当我们观察的图像时，曲线在任意点的切线斜率就等于在该点的高度。

第二部分的几何意义:

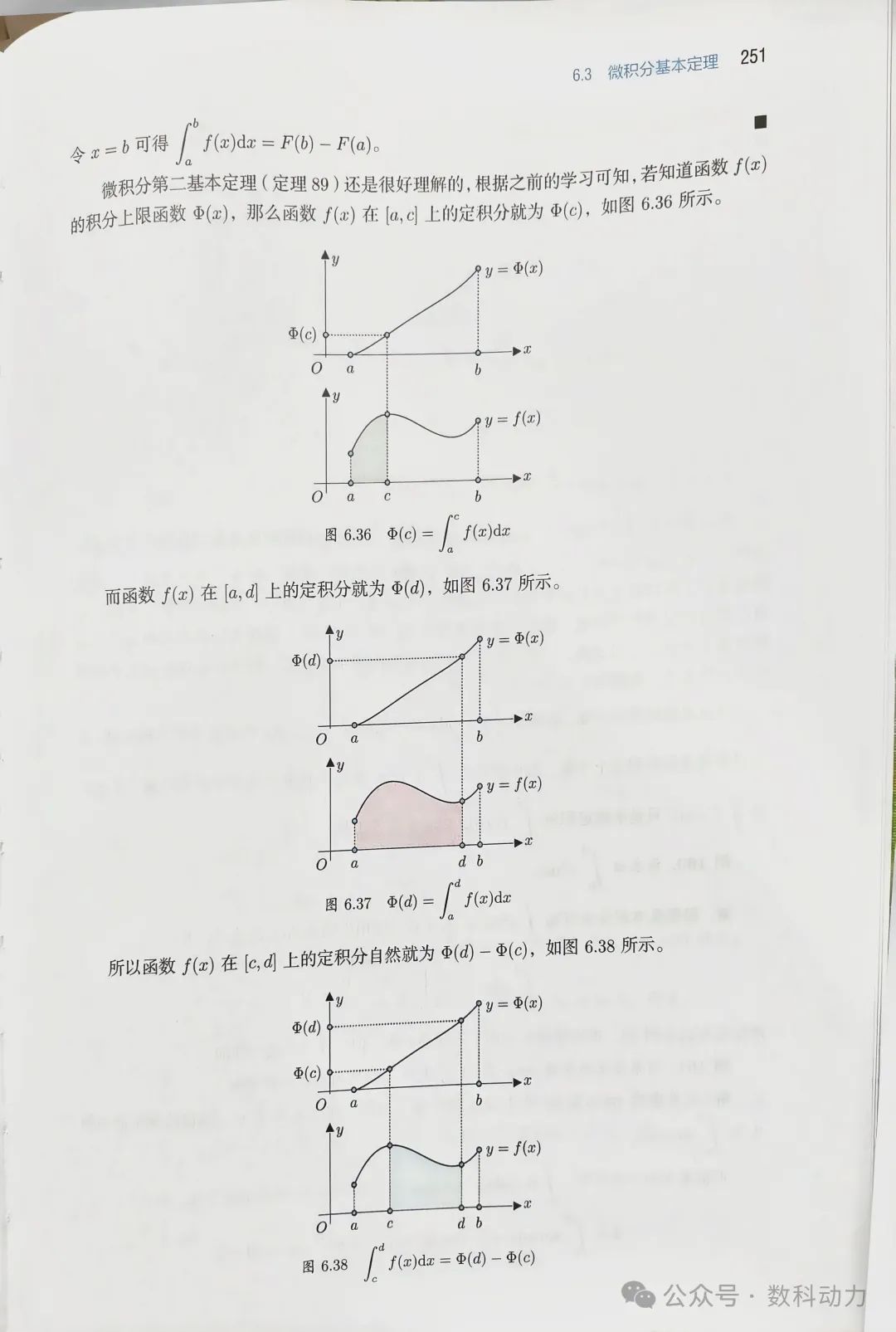
第二部分的定积分代表了函数在区间下方的总面积。这个面积可以通过计算原函数在点的值减去在点的值来获得，即。

这表明，定积分实际上测量的是函数的图形与轴之间，从到这一区间的垂直距离的累加。当在区间内始终非负时，这个面积就是直观上的几何面积；当取负值时，这部分可以视为“负面积”，从总面积中减去。

长按二维码—识别—关注