1.基于概率统计的Bayes分类器
因为在实际分类中由于考虑的侧重点不同或者关心的点不一样导致不能使用同一决策去解决所有的事件的分类,所以需要根据不同的准测函数选择不同的分类决策(基于最小错误率的Bayes决策,基于最小风险的Bayes决策)进行分类,在Bayes分类器中将不同的侧重分为错误率和风险俩个方面,最终通过取舍选择不同决策以求达到自己最理想的分类。
- 先验概率P(w)
即-针对M事件出现可能性而言,不考虑其他任何条件就直接进行事件的分类,所以所提供的信息太少。如:药品公司生产的药,显然一般情况下合格的药品要比不合格的药品的数量所占比例大,所以就容易直接将所有药品都归类为合格的药品,这样并不能很好的将合格和不合格的药品进行分类。
- 类概率密度函数P(X|w)
指-已知某类别的特征空间中出现特征X的概率密度,即第w类样品中它的属性X是如何分布的。(在大多数情况下,类条件概率密度函数可以采用多维变量的正太概率密度函数来模拟)。
- 后验概率P(w|X)
即-可能出现多类别事件出现同一特征的情况,这时就需要判断在条件X出现的条件下,样品为w的概率是多少,而这个后验概率就是使用Bayes公式计算获得的。公式如下:
其中P(Bi)和P(Bj)是指事件Bi和Bj的先验概率,即P(Bi)=Bi/B,P(Bj)=Bj/B;P(A|Bi)和P(A|Bj)是类条件概率密度,指在类Bi和Bj的特征空间中,出现特征A的概率。
使用此种分类器必须要知道有关样品的总体分布知识,包括各类的先验概率、类条件概率密度函数、后验概率,并以这些作为产生判别函数的依据,设计出相应的判别函数与决策面,这种方法称为参数判别式方法。这样,一旦待测试分类样品的特征向量值X已知,就可以确定X对各类的后验概率,也就可以按照相应的准则计算与分类。所以这种分类方法只能用在有统计知识的场合,








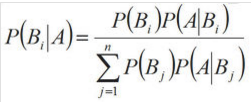
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








