数据结构（C++） 二叉树模板类<链表存储表示>

1.二叉树

递归定义：一颗二叉树是结点的有限的集合，该集合或者为空或者是由一个根节点加上两颗分别称为左子树和右子树、互不相交的二叉树的组合。
二叉树的左右子树都还是二叉树，到达空子树的时候递归定义结束。许多基于二叉树的算法都利用了这个递归特性。
二叉树的特点是每个节点最多有两个子女,分别称为左右子女。在二叉树中不存在度数大于2的节点，并且二叉树的子树有左右之分，其子树的次序不能颠倒。

2.BinaryTree.h文件

#ifndef BINARYTREE_H
#define BINARYTREE_H
#include<stack>
#include<iostream>
#include<stdlib.h>
#include<istream>
#include<queue>
#include<stack>
using namespace std;
//节点结构体
template <class T>
struct BinTreeNode
{
    T data ;
    BinTreeNode<T> *leftChild;
    BinTreeNode<T> *rightChild;
    BinTreeNode():leftChild(NULL),rightChild(NULL) {}
    BinTreeNode(T x,BinTreeNode<T> *l=NULL,BinTreeNode<T> *r=NULL):leftChild(l),rightChild(r),data(x) {}
};
//后序遍历的非递归算法用到的节点结构体
template <class T>
struct stacknode
{
    BinTreeNode<T> *ptr;
    int tag ;
    stacknode(BinTreeNode<T> *n=NULL):ptr(n),tag(1) {}
};

//二叉树类

template <class T>
class BinaryTree
{
public:
    //根指针
    BinTreeNode<T> *root;
    /** Default constructor */
    BinaryTree():root(NULL) {}
    //拷贝构造函数
    BinaryTree(const BinaryTree<T> &s)
    {
        root=Copy(s.root);
    }
    ~BinaryTree()
    {
        destroy(root);
    }
    //判断二叉树是否为空
    bool IsEmpty()
    {
        return (root!=NULL)?true:false;
    }
    //返回父节点
    BinTreeNode<T> *Parent(BinTreeNode<T> *current)
    {
        return (root==NULL||root==current)?NULL:Parent(root,current);
    }
    //返回左节点
    BinTreeNode<T> *LeftChild(BinTreeNode<T> *current)
    {
        return (current==NULL)?NULL:current->leftChild;
    }
    //返回右节点
    BinTreeNode<T> *RightChild(BinTreeNode<T>*current)
    {
        return(current==NULL)?NULL:current->rightChild;
    }
    //返回树的高度
    int Height()
    {
        return Height(root);
    }
    //返回节点数
    int Size()
    {
        return Size(root);
    }
    //获得根节点
    BinTreeNode<T> * getRoot ()
    {
        return root;
    }
递归算法遍历二叉树
//    //前序遍历
//    void preOrder(void(*visit)(BinTreeNode<T> *p))
//    {
//        //递归算法
//        preOrder(root,visit);
//    }
//    //中序遍历
//    void inOrder(void(*visit)(BinTreeNode<T> *p))
//    {
//        inOrder(root,visit);
//    }
//    //后序遍历
//    void postOrder(void(*visit)(BinTreeNode<T> *p))
//    {
//        postOrder(root,visit);
//    }


//每一次访问一个节点后，在向左子树遍历下去之前，
//利用这个栈记录该节点的右子女（如果有的话）节点地址，
//以便左子树退回时可以直接从栈中取出右子树的根节点，继续其右子树的前序遍历
    void preOrder(void(*visit)(BinTreeNode<T> *p))
    {
        stack<BinTreeNode<T> *> nodes;
        BinTreeNode<T> *temp=root;
        nodes.push(NULL);
        while(temp!=NULL)
        {
            visit(temp);
            if(temp->rightChild!=NULL)
            {
                nodes.push(temp->rightChild);
            }
            if(temp->leftChild!=NULL)
            {
                temp=temp->leftChild;
            }
            else
            {
                temp=nodes.top();
                nodes.pop();
            }
        }
    }
    //中序遍历
    //在一棵子树中首先访问的是中序下的第一个节点
    //它位于从根开始的沿着leftchild链走到最左下角的节点，该节点的leftchild为NULL。
    //访问完他的数据之后，再遍历它的右子树。如果此右子树又是二叉树，则重复上面的过程，直到该子树遍历完毕。
    void inOrder(void(*visit)(BinTreeNode<T> *p))
    {
        stack<BinTreeNode<T> *> nodes;
        //遍历指针，从根节点开始
        BinTreeNode<T> *temp=root;
        do
        {
            //遍历指针未到最左下的节点，不空
            while(NULL!=temp)
            {
                //该子树沿途节点进栈
                nodes.push(temp);
                temp=temp->leftChild;
            }
            if(!nodes.empty())
            {
                //栈不为空的时候退栈，访问根节点，遍历指针进入右子女节点
                temp=nodes.top();
                visit(temp);
                nodes.pop();
                temp=temp->rightChild;
            }
        }
        while(NULL!=temp||!nodes.empty());
    }
    //后序遍历
    //后序遍历比先前的两种遍历要复杂得多，在遍历完左子树之后还不能访问根节点，
    //需要再遍历右子树，等到右子树遍历完毕之后才能访问根节点。所以在栈工作记录中一定先表明刚才是在左子树<1>还是在右子树<2>中。
    //首先使用栈暂存根节点的地址，再向左子树遍历下去，此时根节点的tag为1，当访问完根节点的左子树之后从左子树退回，还要去遍历右子树
    //此时改跟的tag为2.
    //从右子树中退出时才能访问位于栈顶的根节点的值。
    void postOrder(void(*visit)(BinTreeNode<T> *p))
    {
        stack<stacknode<T> > nodes;
        stacknode<T> temp;
        BinTreeNode<T> *p=root;
        do
        {
            while(NULL!=p)
            {
                temp.ptr=p;
                temp.tag=1;
                nodes.push(temp);
                p=p->leftChild;
            }
            int continue1=1;
            while(continue1&&!nodes.empty())
            {
                temp=nodes.top();
                nodes.pop();
                p=temp.ptr;
                switch(temp.tag)
                {
                case 1:
                    temp.tag=2;
                    nodes.push(temp);
                    continue1=0;
                    p=p->rightChild;
                    break;
                case 2:
                    visit(p);
                    break;
                }
            }

        }
        while(!nodes.empty());
    }




    //层次遍历
    //层次遍历从二叉树的根节点开始，自上向下，自左向右，分层依次访问树中的各个节点、

    void levelOrder(void (*visit)(BinTreeNode<T> *p))
    {
        queue<BinTreeNode<T> *> nodes;
        BinTreeNode<T> *temp=root;
        BinTreeNode<T> *tnode;
        nodes.push(temp);
        while(!nodes.empty())
        {
            tnode=nodes.front();
            nodes.pop();
            visit(tnode);
            if(NULL!=tnode->leftChild)
            {
                nodes.push(tnode->leftChild);
            }
            if(NULL!=tnode->rightChild)
            {
                nodes.push(tnode->rightChild);
            }
        }
    }
    //插入新元素
    void  Insert(const T &item) {}
    //搜索
    BinTreeNode<T> *Find(T &item) const {}
    void CreateBinTree()
    {
        CreateBinTree(root);
    }
    //前序遍历输出

    void Traverse(BinTreeNode<T> * subTree)
    {
        if(NULL!=subTree)
        {

            cout<<subTree->data<<" ";
            //递归输出subTree的左子树
            Traverse(subTree->leftChild);
            //递归输出subTree的右子树
            Traverse(subTree->rightChild);
        }
    }

protected:

    //利用二叉树前序遍历建立二叉树
    void CreateBinTree(BinTreeNode<T> *&subTree)
    {
        T item;
        if((cin>>item)&&item!="#")
        {
            subTree=new BinTreeNode<T>(item);
            if(subTree==NULL)
            {
                cerr<<"存储分配错误！"<<endl;
                exit(1);
            }
            CreateBinTree(subTree->leftChild);
            CreateBinTree(subTree->rightChild);
        }
        else
        {
            //封闭指向空子树的指针
            subTree=NULL;
        }
    }
    //插入
    bool Insert(BinTreeNode<T> *&subTree,const T& x) {}
    //搜索
    bool Find(BinTreeNode<T> *subTree,const T& x)const {}
    //根据值查找结点
    BinTreeNode<T>* Find(BinTreeNode<T> *subTree,const T &x ) {}
    //拷贝
    BinTreeNode<T> *Copy(BinTreeNode<T> *originnode)
    {
        if(originnode==NULL)
        {
            return NULL;
        }
        BinTreeNode<T> *temp=new BinTreeNode<T>();
        temp->data=originnode->data;
        temp->leftChild=originnode->leftChild;
        temp->rightChild=originnode->rightChild;
        return temp;
    }
    //析构函数
    void destroy(BinTreeNode<T> *subTree)
    {
        if(subTree!=NULL)
        {
            destroy(subTree->leftChild);
            destroy(subTree->rightChild);
            delete subTree;
        }
    }
    //返回父节点，从节点subTree开始，搜索current节点的父节点
    BinTreeNode<T> *Parent(BinTreeNode<T> *subTree,BinTreeNode<T> *current)
    {
        if(current==NULL)
            return NULL;
        //找到返回父节点
        if(subTree->leftChild==current||subTree->rightChild==current)
            return subTree;
        BinTreeNode<T> *p;
        //在左子树种递归查找
        if((p=Parent(subTree->leftTree,current))!=NULL)
            return p;
        //在右子树种递归查找
        else
            return Parent(subTree->rightChild,current);
    }
    //返回树的高度
    int Height(BinTreeNode<T> *subTree)
    {
        if(subTree==NULL)
        {
            return 0;
        }
        else
        {
            int leftHieght=Height(subTree->leftChild);
            int rightHeight=Height(subTree->rightChild);
            return (leftHieght>rightHeight)?leftHieght+1:rightHeight+1;
        }

    }
    //返回根节点
    int Size(BinTreeNode<T> *subTree) const
    {
        if(subTree==NULL)
        {
            //递归结束，节点个数为0
            return 0;
        }
        else
        {
            return 1+Size(subTree->leftChild)+Size(subTree->rightChild);
        }
    }
    //前序遍历
    void preOrder(BinTreeNode<T>*subTree,void(*visit)(BinTreeNode<T> *p))
    {
        if(subTree!=NULL)
        {

            visit(subTree);
            preOrder(subTree->leftChild,visit);
            preOrder(subTree->rightChild,visit);
        }
    }
    //中序遍历
    void inOrder(BinTreeNode<T> *subTree,void(*visit)(BinTreeNode<T> *p))
    {
        //递归函数,=NULL是终止递归条件
        if(subTree!=NULL)
        {
            inOrder(subTree->leftChild,visit);
            visit(subTree);//访问根节点
            inOrder(subTree->rightChild,visit);
        }
    }
    //后序遍历
    void postOrder(BinTreeNode<T> *subTree,void(*visit)(BinTreeNode<T> *p))
    {
        if(subTree!=NULL)
        {
            postOrder(subTree->leftChild,visit);
            postOrder(subTree->rightChild,visit);
            visit(subTree);
        }
    }
};

#endif // BINARYTREE_H

3.main函数

#include <iostream>
#include<BinaryTree.h>
#include<string>
template <class T>
void visit(BinTreeNode<T> *p );
using namespace std;
int main()
{
    BinaryTree<string> *bin=new BinaryTree<string>();
    bin->CreateBinTree();
    if(bin->IsEmpty())
    {

        cout<<"当前树不为空,输出所有节点："<<endl;
        bin->Traverse(bin->root);
        cout<<endl;
        cout<<"当前树的高度是："<<bin->Height()<<endl;
        cout<<"当前树的大小是："<<bin->Size()<<endl;
        cout<<"前序遍历："<<endl;
        bin->preOrder(visit);
        cout<<"\n中序遍历："<<endl;
        bin->inOrder(visit);
        cout<<"\n后序遍历："<<endl;
        bin->postOrder(visit);
        cout<<endl;
        cout<<"树的根节点是："<<bin->getRoot()->data;
    }
    delete bin;
    return 0;
}
template < class T>
void visit(BinTreeNode<T> *p )
{
    cout<< p->data<<"  ";
}

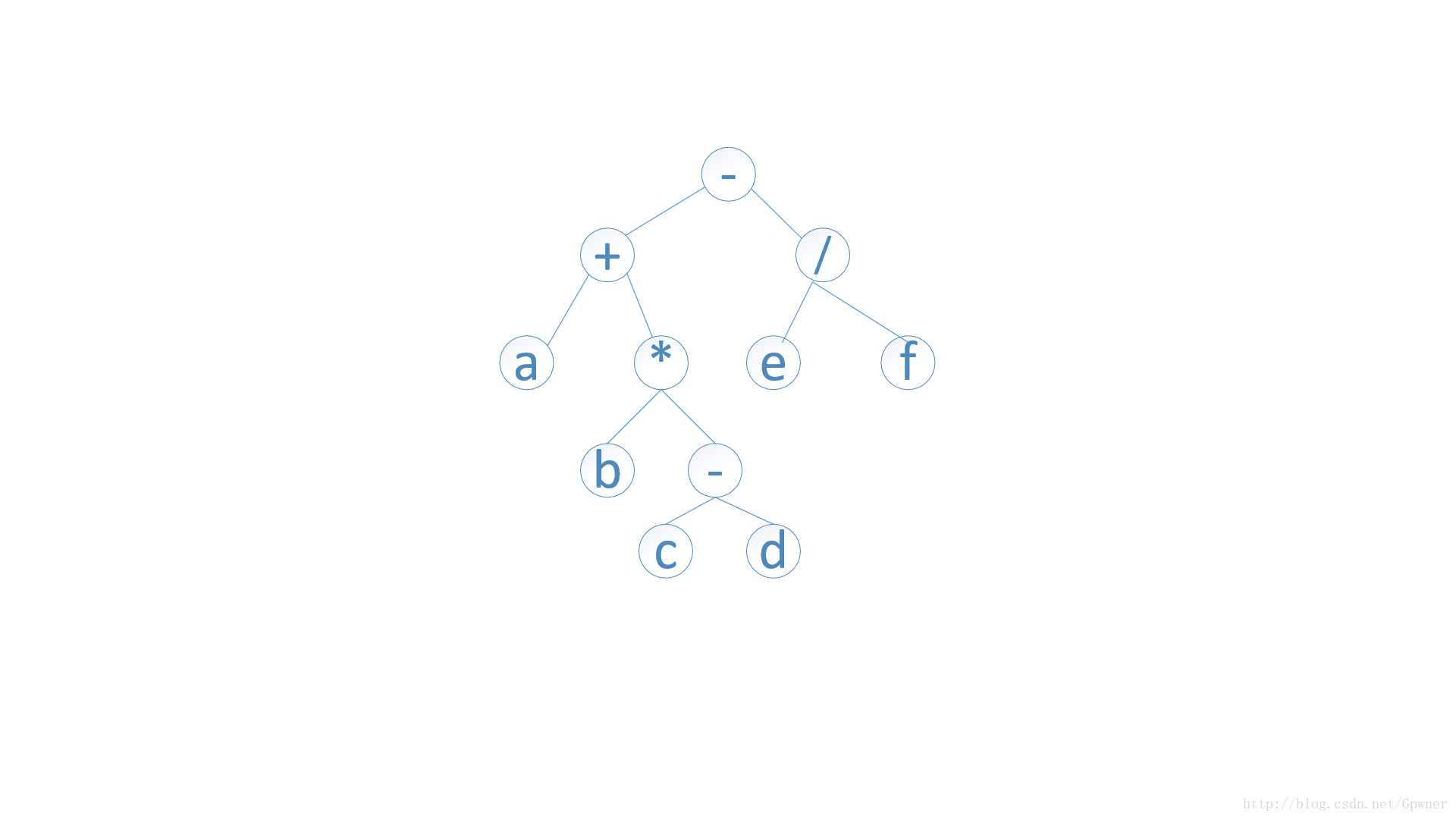
下面是一颗二叉树：

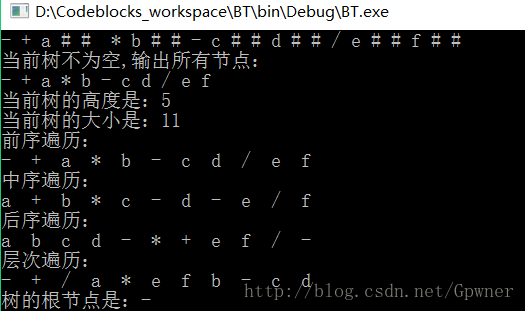
模板类存储运行结果：

完整的工程代码，请点击这里