# curling 2.0-poj3009
### 大哥鼎力推荐的最佳区分DFS和BFS的题目,供瞻仰
> 题目描述:冰球游戏,在如下的棋盘中,指定一个起点S、一个终点G,问最少需要多少次操作能使得冰球从S运动到G。冰球的运动遵循如下原则:
> * 只能沿XY方向运动,不能沿斜线
> * 冰球可以被移动的前提是下一个位置不能是block
> * 冰球在某个方向上会保持运动除非出现一下三种情况:遇到block,冰球撞击后block消失;出边界;到达目标点G。
> * 操作数不能超过10次

具体样例如下(a)为运动路线,(b)为运动后block的状态
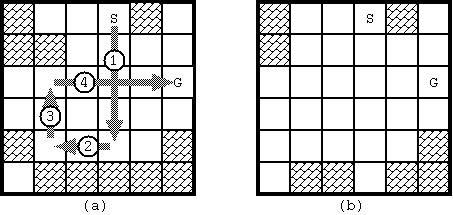
> 输入:w,h(w为列数,h为行数)
> hxw的矩阵,矩阵值有三种:
> * 0 空
> * 1 block
> * 2 起点
> * 3 终点
> 输出:最小操作数使得冰球从S到G
### 解题思路:
找最短路径最自然的想法是用BFS,但用BFS解此题,最大的问题在于**block会消失**,这个条件会导致当并行计算多个路径时,每个路径对应的棋盘状态不同,也即BFS对应的每个需要入队列的状态都需要保
### 大哥鼎力推荐的最佳区分DFS和BFS的题目,供瞻仰
> 题目描述:冰球游戏,在如下的棋盘中,指定一个起点S、一个终点G,问最少需要多少次操作能使得冰球从S运动到G。冰球的运动遵循如下原则:
> * 只能沿XY方向运动,不能沿斜线
> * 冰球可以被移动的前提是下一个位置不能是block
> * 冰球在某个方向上会保持运动除非出现一下三种情况:遇到block,冰球撞击后block消失;出边界;到达目标点G。
> * 操作数不能超过10次

具体样例如下(a)为运动路线,(b)为运动后block的状态

> 输入:w,h(w为列数,h为行数)
> hxw的矩阵,矩阵值有三种:
> * 0 空
> * 1 block
> * 2 起点
> * 3 终点
> 输出:最小操作数使得冰球从S到G
### 解题思路:
找最短路径最自然的想法是用BFS,但用BFS解此题,最大的问题在于**block会消失**,这个条件会导致当并行计算多个路径时,每个路径对应的棋盘状态不同,也即BFS对应的每个需要入队列的状态都需要保








 这篇博客介绍了POJ3009编程题目,这是一个关于冰球在棋盘上移动的最短路径问题。博主推荐使用DFS而非BFS,因为DFS在处理block消失的情况下有更好的效率,同时提供了问题描述、样例、解题思路和C++代码实现。
这篇博客介绍了POJ3009编程题目,这是一个关于冰球在棋盘上移动的最短路径问题。博主推荐使用DFS而非BFS,因为DFS在处理block消失的情况下有更好的效率,同时提供了问题描述、样例、解题思路和C++代码实现。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1010
1010

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








