活动网络——AOE网络

AOE网络：如果在有向无环图中用有向边表示一个工程中的各项活动，用有向边上的权值表示活动的持续时间，用顶点表示事件，则这种有向图叫做用边表示活动的网络，简称AOE网络。

AOE网络的用途

（1）完成整个工程至少需要多长时间

 （2）为缩短工程所需的时间，应加快哪些活动

关键路径：完成整个工程所需的时间取决于从源点到汇点的最长路径长度，这条路径最长的路径就称为关键路径。（Critical Path）;

常用的量：（1）事件Ei的最早可能开始时间，记为Ee[i].是从源点到顶点Ei的最长路径长度

                   （2）事件Ei的最迟可能开始时间，记为El[i].El[i]是在保证汇点En-1在Ee[n-1]时刻完成的前提下，事件Ei允许开始的最迟时间，它等于Ee[n-1]减去从Ei到En-1的最长路径长度。

                    （3）活动ak的最早可能开始时间，记为e[k]。设活动在有向边<Ei,Ej>上，e[k]=Ee[i].

                     （4）活动ak最迟允许开始的时间，记为l[l].   l[k]=El[j]-dur<Ei,Ej>的值。

松弛时间：l[k]-e[k]

求Ee[i]的递推公式，从Ee[0]=0开始，向前递推：

Ee[i]=max{Ee[j]+dur(<Ej,Ei>)}.

求El[i]的递推公式。从El[n-1]=Ee[n-1]开始，反向递推

El[i]=min{  El[j]-dur(<Ei,Ej>)  }.

这两个递推公式必须在拓扑有序及逆拓扑有序的前提下进行。所谓逆拓扑有序，就是首先输出出度为0的顶点，以相反的次序输出拓扑排序序列，这种排序称为逆拓扑排序。

也就是说，在计算Ee[i]时，Ei的所有前驱顶点Ej的Ee[j]都已经求出。反之，在计算El[i]时，Ei的所有后继顶点El[j]都已经求出

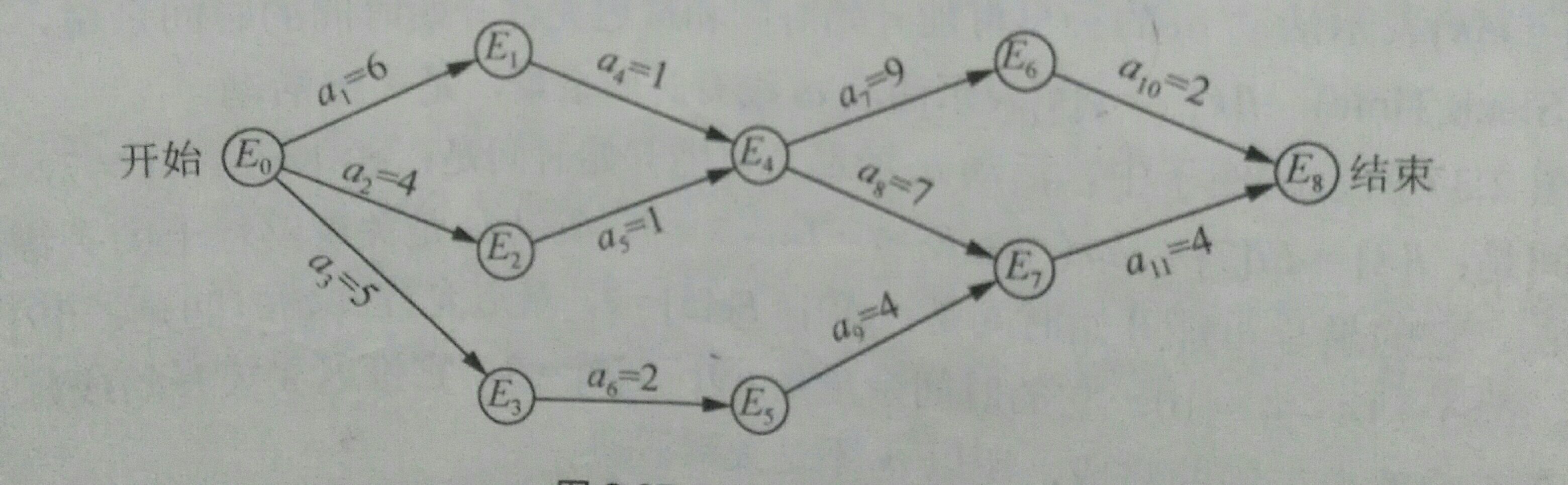
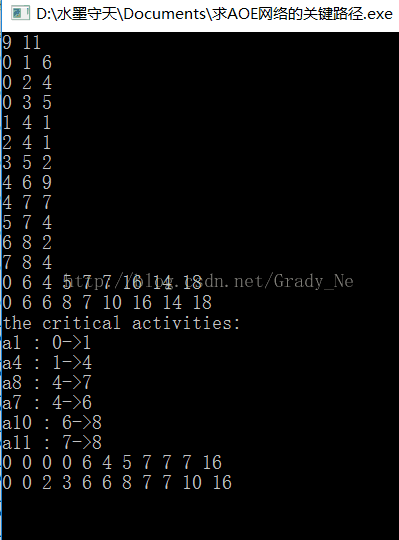
例题：求如图所示的AOE网络的关键路径并输出。首先输入顶点个数n和边个数m，然后依次输入每条边

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
#define MAXN 100///顶点数目的最大值
#define MAXM 200///边的数目的最大值
struct ArcNode
{
    int to,dur,no;///no为活动序号
    ArcNode *next;
};
int n,m;
ArcNode *list1[MAXN];///出边表的表头指针
ArcNode *list2[MAXN];///入边表的表头指针
int count1[MAXN];///各顶点的入度
int count2[MAXN];///各顶点的出度
int Ee[MAXN];///各事件最早可能开始的时间
int El[MAXN];///各事件允许开始的最迟时间
int e[MAXM];///各活动最早可能开始的时间
int l[MAXM];///各活动允许最晚可以开始的时间
void CriticalPath();
int main()
{
    int i,j;
    int u,v,w;
     while(scanf("%d%d",&n,&m)!=EOF)///顶点数和边数
    {
        if(n==0&&m==0) break;
       memset(list1,0,sizeof(list1));
       memset(list2,0,sizeof(list2));
       memset(count1,0,sizeof(count1));
       memset(count2,0,sizeof(count2));
       ArcNode *temp1,*temp2;
       for(i=0;i<m;i++)
       {
           scanf("%d%d%d",&u,&v,&w);
           count1[v]++;
           temp1=new ArcNode;///构造邻接表
           temp1->to=v;
           temp1->dur=w;
           temp1->no=i+1;
           temp1->next=NULL;
           if(list1[u]==NULL)
            list1[u]=temp1;
           else
           {
               temp1->next=list1[u];
               list1[u]=temp1;
           }
           count2[u]++;
           temp2=new ArcNode;///构造逆邻接表
           temp2->to=u;
           temp2->dur=w;
           temp2->no=i+1;
           temp2->next=NULL;
           if(list2[v]==NULL)
            list2[v]=temp2;
           else
           {
               temp2->next=list2[v];
               list2[v]=temp2;
           }
       }
       CriticalPath();
       ///释放边链表上各边结点所占用的空间
       for(i=0;i<n;i++)
       {
           temp1=list1[i];
           temp2=list2[i];
           while(temp1!=NULL)
           {
               list1[i]=temp1->next;
               delete temp1;
               temp1=list1[i];
           }
           while(temp2!=NULL)
           {
               list2[i]=temp2->next;
               delete temp2;
               temp2=list2[i];
           }
       }

    }
    return 0;
}
void CriticalPath()
{
    ///拓扑排序求Ee；
     int i,j,k;
     int top1=-1;
     ArcNode *temp1;
     memset(Ee,0,sizeof(Ee));
     for(i=0;i<n;i++)///找出入度为0的点
     {
         if(count1[i]==0)
         {
             count1[i]=top1;
             top1=i;
         }
     }
     for(i=0;i<n;i++)
     {
         if(top1==-1)
         {
             printf("Network has a cycle\n");
             return ;
         }
         else
            {
               j=top1;
              top1=count1[top1];
              temp1=list1[j];
           while(temp1!=NULL)
           {
               k=temp1->to;
               count1[k]--;
               if(count1[k]==0)
               {
                   count1[k]=top1;
                   top1=k;
               }
               if(Ee[j]+temp1->dur>Ee[k])
                Ee[k]=Ee[j]+temp1->dur;
               temp1=temp1->next;
           }
        }
     }
     ///逆拓扑排序求El;
     int top2=-1;
     ArcNode *temp2;
     for(i=0;i<n;i++)///找出出度为0的顶点
     {
         El[i]=Ee[n-1];///初始化为已知的最大值
         if(count2[i]==0)
         {
             count2[i]=top2;
             top2=i;
         }
     }
     for(i=0;i<n;i++)
     {
         j=top2;
         top2=count2[top2];
         temp2=list2[j];
         while(temp2!=NULL)
         {
             k=temp2->to;
             count2[k]--;
             if(count2[k]==0)
             {
                 count2[k]=top2;
                 top2=k;
             }
             if(El[j]-temp2->dur<El[k])
                El[k]=El[j]-temp2->dur;
             temp2=temp2->next;
         }
     }
      ///输出Ee[i]和El[i]
     for(i=0;i<n;i++)
        cout<<Ee[i]<<" ";
     cout<<endl;
     for(i=0;i<n;i++)
        cout<<El[i]<<" ";
        cout<<endl;
     ///求各种活动的e[k]和l[k];
     memset(e,0,sizeof(e));
     memset(l,0,sizeof(l));
     printf("the critical activities:\n");
     for(i=0;i<n;i++)
     {
         temp1=list1[i];
         while(temp1!=NULL)
         {
             j=temp1->to;///有向边<i,j>;
             k=temp1->no;
             e[k]=Ee[i];
             l[k]=El[j]-temp1->dur;
              if(e[k]==l[k])
                {
                     printf("a%d : %d->%d\n",k,i,j);
                }
             temp1=temp1->next;
         }
     }
     ///输出e[i]和l[i]的值
      for(i=0;i<m;i++)
        cout<<e[i]<<" ";///为啥前四个都为0？？因为是最早可能开始的时间
     cout<<endl;
     for(i=0;i<m;i++)
        cout<<l[i]<<" ";
     cout<<endl;
}

测试数据：

TMD书上的测试数据竟然给错，还好有超哥相助，多谢超哥