本文首先介绍了概率论里在数学建模中的常用分布,包括连续型分布中的均匀分布、指数分布、正态分布以及离散型分布中的二项分布、泊松分布,并针对各种分布列举了一些对应的遵循该分布的例子。然后列举了十多种Matlab里按照各种要求生成随机数、随机序列的方法,并简要介绍了excel里生成随机数的方法。最后列举了一个需要用到生成随机数知识的例子。
一、常用概率分布与服从该分布的事件举例
在实际生活中,有一些事情的发生遵循某些概率分布。因此可以用某些概率分布模型来刻画某些事件。本节简单介绍了一些概率论基础里的概率分布,与可用其刻画的一些事件。数学理论部分不详述,建议参考概率论教科书。
1、连续型分布
(1)、均匀分布(Uniform)
均匀分布是概率统计中的重要分布之一。顾名思义,均匀,表示可能性相等的含义。在实际问题中,当我们无法区分在区间[a,b]内取值的随机变量X取不同值的可能性有何不同时,我们就可以假定X服从[a,b]上的均匀分布。
概率密度函数:
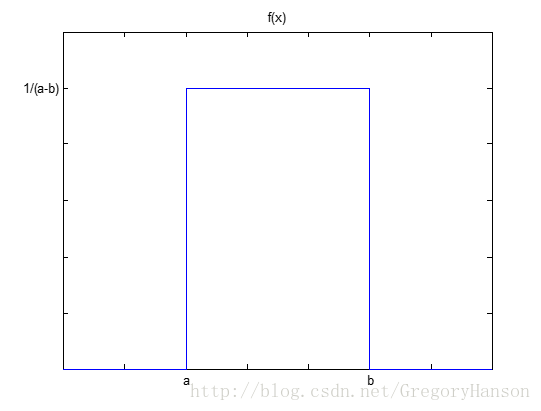
分布函数:
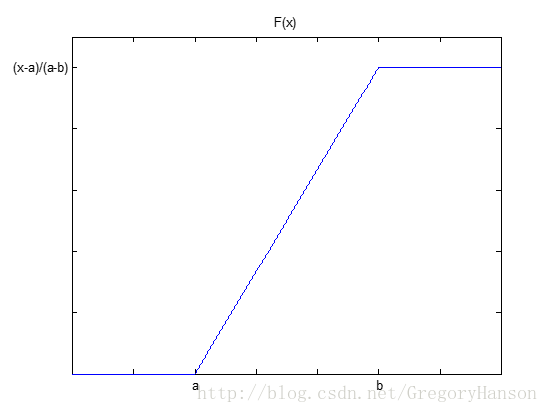
适用模型:
在某区间内某事件发生的概率相等的问题。
(2)、指数分布
在概率理论和统计学中,指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。它是几何分布的连续模拟,它具有无记忆的关键性质。除了用于分析泊松过程外,还可以在其他各种环境中找到。
概率密度函数:
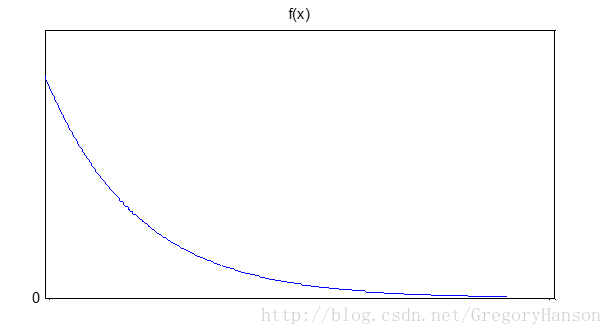
分布函数:
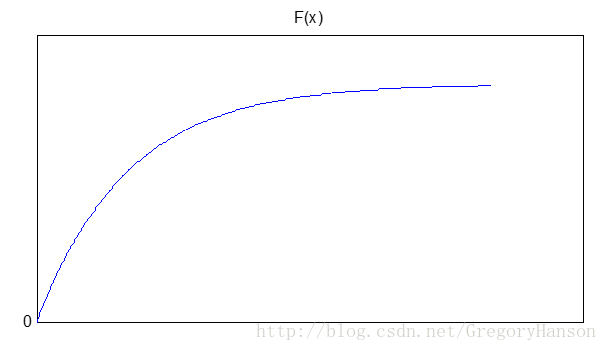
适用模型:
在电子元器件的可靠性研究中,通常用于描述对发生的缺陷数或系统故障数的测量结果。这种分布表现为均值越小,分布偏斜的越厉害。可以近似地作为
高可靠性的复杂部件、机器或系统的失效分布模型,特别是在部件或机器的整机试验中得到广泛的应用。
(3)、正态分布(Normal)(又称高斯分布)
正态分布是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。正态曲线呈钟型,两头低,中间高,左右对称。因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)
。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
概率密度函数:
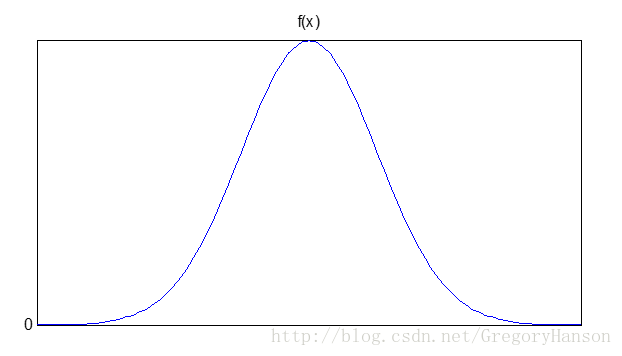
分布函数:
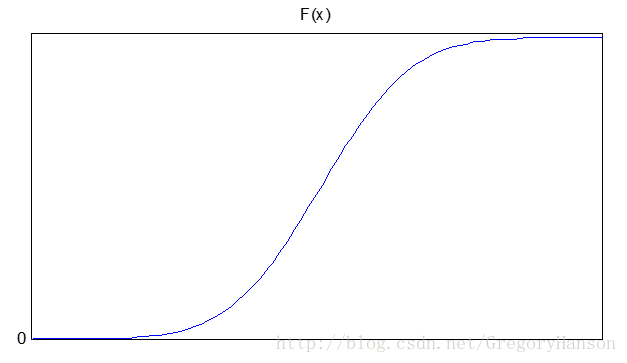
适用模型:
社会人群生活水平
人群身高分布
通货膨胀率和能源价格
考试成绩及学生综合素质研究(教育统计学统计规律表明,学生的智力水平,包括学习能力,实际动手能力等呈正态分布)
医学参考值(某些医学现象,如同质群体的身高、红细胞数、血红蛋白量,以及实验中的随机误差,呈现为正态或近似正态分布;有些指标(变量)虽服从偏态分布,但经数据转换后的新变量可服从正态或近似正态分布,可按正态分布规律处理)
2、离散型分布
(1)、二项分布(伯努利概型)
二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
在n重伯努利试验中,设事件A发生的概率为p,事件A发生的次数是随机变量,设为X,则X可能取值为0,1,2,…,n
分布律:
n=20,p=0.7时分布图像如下:
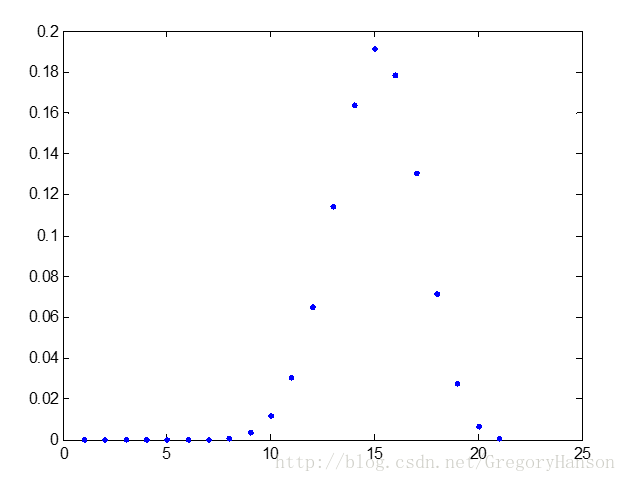
适用模型:
打枪、投篮问题(实验n次发生k次)
设备使用设备故障等确定基数下发生或不发生问题
(2)、泊松分布(n趋于无穷时二项分布的近似)
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。可参考《随机过程》中的泊松过程进一步学习。
分布律:
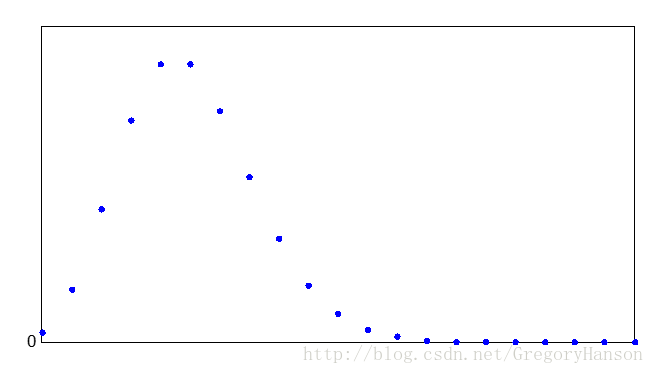
适用模型:
交通事故
某一服务设施在一定时间内到达的人数
电话交换机接到呼叫的次数
汽车站台的候客人数,
机器出现的故障数
自然灾害发生的次数
一块产品上的的缺陷数
显微镜下单位分区的细菌分布数
一个医院中里特定时间段接纳的病人总数
举例:
采用0.05J/㎡紫外线照射大肠杆菌时,每个基因组(~4×106核苷酸对)平均产生3个嘧啶二体。实际上每个基因组二体的分布是服从泊松分布的,因此:
P(0)是未产生二体的菌的存在概率,由于该菌株每个基因组有一个二体就是致死量,因此就意味着全部死亡的概率。
二、随机数生成方法
1、在matlab中生成随机数
(1)rand函数——按照0~1的均匀分布生成随机数
>> m=2;n=3;
>> r1=rand(m,n) %按照0~1间的均匀分布生成m行n列的伪随机数
r1 =
0.8147 0.1270 0.6324
0.9058 0.9134 0.0975
>> r2=rand(m,n,'double') %按照0~1间的均匀分布生成m行n列指定精度的伪随机数,参数还可以是'single'
r2 =
0.2785 0.9575 0.1576
0.5469 0.9649 0.9706(2)randi函数——按照均匀分布生成随机整数
>> iMax=5;iMin=2;m=2;n=3;
>> r1=randi(iMax) %生成1~iMax均匀分布的伪随机整数
r1 =
5
>> r2=randi(iMax,m,n) %生成1~iMax间均匀分布的m*n大小的随机整数矩阵
r2 =
3 1 5
5 3 4
>> r3=randi([iMin iMax],m,n) %生成iMin~iMax间均匀分布的m*n大小的随机整数矩阵
r3 =
5 2 5
4 5 4(3)unifrnd函数——按照均匀分布的生成随机浮点数
>> a=2;b=6;
>> r1=unifrnd(a,b) %产生一个[a,b]均匀分布的随机数
r1 =
3.1077
>> r2=unifrnd(a,b,m,n) %产生一个大小为m*n的在[a,b]间均匀分布的随机数矩阵
r2 =
2.1847 5.2938 3.2684
2.3885 4.7793 5.8009(4)unidrnd函数——按照均匀分布生成随机自然数
>> N=5;m=2;n=3;
>> r1=unidrnd(N,m,n) %产生一个1~N间均匀分布的大小为m*n的随机数矩阵
r1 =
1 2 4
3 4 1(5)normrnd函数——按照正态分布生成随机数
>> MU=0;SIGMA=1;m=2;n=3;
>> r1=normrnd(MU,SIGMA,m,n) %按照均值为MU,方差为SIGMA的正态分布生成一个大小为m*n的随机数矩阵
r1 =
0.0774 -1.1135 1.5326
-1.2141 -0.0068 -0.7697
>> r2=normrnd([1 2 3;4 5 6],0.1,2,3) %按照期望依次为[1 2 3;4 5 6],方差为0.1的正态分布生成一个大小为2*3的随机数矩阵
r2 =
1.0371 2.1117 3.0033
3.9774 4.8911 6.0553(6)randn函数——按照标准正态分布生成随机数(均值为0,方差为1),主要语法同rand函数
(7)binornd函数——按照二项分布生成随机数
>> N=10;P=0.5;m=2;n=3;
>> binornd(N,P,m,n) %产生m*n均值为N*P的矩阵
ans =
6 4 6
4 6 4(8)poissrnd函数——按照泊松分布生成随机数
>> lambda=3;
>> r1=poissrnd(lambda) %按照lambda为3的泊松分布生成一个随机数
r1 =
3
>> m=2;n=3;
>> r2=poissrnd(lambda,m,n) %按照lambda为3的泊松分布生成一个大小为m*n的随机数矩阵
r2 =
1 3 3
3 3 1(9)random函数——生成指定的常用分布的随机数,一般形式为:
y = random('分布的英文名',A1,A2,A3,m,n)表示生成 m 行 n 列的 m × n 个参数为 ( A1 , A2 , A3 ) 的该分布的随机数。
>> r1=random('Normal',0,1,2,4) %按照期望为0,标准差为1的正态分布生成一个大小为2*4的随机数矩阵
r1 =
-0.9792 -0.5336 0.9642 -0.0200
-1.1564 -2.0026 0.5201 -0.0348
>> r2=random('Poisson',1:6,1,6) %依次按照lambda为1到6的泊松分布生成6个随机数
r2 =
0 3 4 1 2 3
(10)randsrc函数——按自定义概率生成随机数(有时候会有意想不到的效果,后面有例题)
>> m=2;n=3;
>> alphabet=[1 5 2 7];prob=[0.2 0.5 0.1 0.2];
>> r1=randsrc(m,n) %生成一个m*n大小的随机数矩阵,元素为随机出现的-1或1,概率各为1/2
r1 =
-1 1 -1
1 1 1
>> r2=randsrc(m,n,alphabet) %输出m*n阶矩阵,元素由alphabet确定,各元素出现概率相等
r2 =
5 1 1
2 2 5
>> **r3=randsrc(m,n,[alphabet;prob]) %prob参数确定了alphabet里每个元素出现的概率**
r3 =
5 1 2
2 7 5(11)randperm函数——生成自然数伪随机序列
>> n=5;k=3;
>> r1=randperm(n) %返回1~n这n个数的一个随机排列
r1 =
4 3 2 5 1
>> r2=randperm(n,k) %返回一个1~n的其中随机k个不重复的数的随机排列,其中k不可以大于n
r2 =
1 5 4
>> old=[1 2 3;4 5 6;7 8 9]
old =
1 2 3
4 5 6
7 8 9
>> new=old(randperm(size(old,1)),:) %对旧矩阵的各列进行重新排列
new =
4 5 6
1 2 3
7 8 9(12)randsample函数
>> n=5;k=3;
>> array=[1 2 3 4 5];
>> r1=randsample(n,k) %和randperm(n,k)功能一样
r1 =
3
1
2
>> r2=randsample(array,k) %从数组array中随机去除k个不相同的数
r2 =
4 1 3
>> replacement=1;
>> r3=randsample(n,k,replacement)
r3 =
5
3
1
>> replacement=0;
>> r3=randsample(n,k,replacement)
r3 =
1
4
2
>> %相似的用法还有randsample(array,k,replacement)
>> old=[1 2 3 4 5]
old =
1 2 3 4 5
>> new=randsample(old,length(old),0) %旧矩阵随机重新排列
new =
3 2 4 5 1
>> n=4;k=10;w=[0.15 0.35 0.35 0.15];
>> r4=randsample(n,k,true,w)'
r4 =
2 3 1 2 3 1 4 3 2 3
>> %w是权重系数,能够根据此权重系数在原数组(或1~n数组)里面选出可能重复的k个数
>> %相似的用法还有 randsample(array,k,true,w)
>> r5=randsample('ACGT',12,true,w)
r5 =
CCTGGCCGGCCT
>> %上面的语句能够产生12个内容为ATCG中的字母的随机字符串,且A出现的可能性为0.15
>> %randsample(s,…)可以用自己提供的随机数stream替换系统默认的随机数,s必须派生自Matlab的RandStream类rendperm与randsample对比:
randperm比randsample更直接更底层,而randsample则是对各种使用的情形进行了封装;randsample可以很方便的实现随机数的权重分布。
(13) 其他分布函数表:

2、在excel中生成随机数
(1)RAND()函数
在单元格中输入=RAND(),回车后单元格即返回了一个0~1的随机数字。
注:同时返回多个随机数是不重复的。
生成指定范围的随机数。假定给定数字范围最小是A,最大是B,公式是 =A+RAND()*(B-A)

(2)RANDBETWEEN()函数
在单元格中输入=RANDBETWEEN(范围下限整数,范围上限整数),回车后单元格即返回了一个随机整数。
注:上限和下限可以不是整数,并且可以是负数。

生成0.01~1之间包含两位小数的随机数

三、matlab中应用随机数的例题
假设班级里有100 名学生,学号1到100顺序排列,由于我们希望每个学生都能尽量被点到,因此一旦某个学生被点到以后,其概率下降,同时提高其他学生被点到的概率。规则如下:
首先假设未进行任何一次点名的时候,每个学生等概率被点到,其次假设每次点名只点一名学生。如果在某次点名中学生i被点到,那么下一次点名的时候学生i 的概率减为当前的一半,另一半概率平均分配给其他同学。
假设每天点30次名放学,第二天以每位同学被点名几率等概的情况开始。请给出一个模拟程序,该程序模拟100天点名,计算这100天内有多少天有一个同学被点名达到或超过了3次?
(题目来源:某北京高校夏令营题目改编)
解法一:(使用randsrc函数)
alphabet = 1:100; % alphabet为每个学生序号
prob = 1/100*ones(1,100);% prob为每个学生被点到的概率
day = 0; % day为同一学生一天内被点到不少于三次的天数
num = zeros(100,30); % num(i,j)记录第i天的第j次点名被点到的学号
for i = 1:100 % 每次循环代表第i天
prob = 1/100*ones(1,100);
for j = 1:30 % 每次循环代表第i天的第j次点名
num(i,j) = randsrc(1,1,[alphabet;prob]);
temp = prob(num(i,j))/2;
prob = prob + temp/99;
prob(num(i,j)) = temp;
end
format short
count = tabulate(num(i,:)); % count(:,2)记录第i天学生各自被点到的次数
if(find(count(:,2)>=3))
day = day +1;
end
end
day解法二:自己编写函数实现生成某种特殊概率的随机数
主函数:
day = 0; % day为同一学生一天内被点到不少于三次的天数
for i = 1:100 % 每次循环代表第i天
stu_p = 1:100;
% 代表初始时100个序号等概率出现,即每个序号出现一次
% 每次点名后会改变,第二天再次初始化
stu_len = ones(1,100);
% stu_len(t)代表第i天序号为t的学生被点到的概率为stu_len(t)%
% 每次点名后会改变,第二天再次初始化位1%
stu_count = zeros(1,100);
% stu_count(t)代表第i天序号为t的学生被点到的次数
for j = 1:30 % 每次循环代表第i天的第j次点名
k = 100*rand(1); % 生成一个连续均匀分布的0~100之间的随机数
if k<stu_p(1)
num = 1; % 记录第i天第j次点名的学生序号
len = stu_p(1); % 区间长度可以理解为此时点到序号1同学的相对概率
else
for t = 2:100
if k>stu_p(t-1) && k<stu_p(t)
num = t; % 记录第i天第j次点名的学生序号
len = stu_p(t) - stu_p(t-1);
% 区间长度可以理解为此时点到序号t同学的相对概率
end
end
end
[stu_p,stu_len] = redis(stu_p,stu_len,num,len);
stu_count(num) = stu_count(num) + 1;
end
if find(stu_count>=3)
day = day + 1;
end
end
day子函数:
function [ stu_p,stu_len ] = redis( stu_p,stu_len,num,len )
% 每次点名后更新一次stu_p,stu_len和stu_count
for t = 1:100 % 更新stu_p
if t == num
if t == 1
stu_p(t) = stu_p(t) - len/2;
else
stu_p(t) = stu_p(t-1) + len/2;
end
else
if t == 1
stu_p(t) = stu_p(t) + len/99;
else
stu_p(t) = stu_p(t-1) + stu_len(t) + len/99;
end
end
end
for t=1:100 % 更新stu_len
if t==1
stu_len(t)=stu_p(t);
else
stu_len(t)=stu_p(t)-stu_p(t-1);
end
end四、本节其他推荐网站
详细介绍了二项分布、泊松分布、均匀分布、指数分布、正态分布等五个常用的概率分布,还贴心地给出了这五种概率分布的应用例题。)
https://wenku.baidu.com/view/440955360b4c2e3f57276312.html
关于通过管理默认(缺省)流来使得两个语句获得相同的随机数,可参考链接http://blog.sina.com.cn/s/blog_4b94ff130100edwh.html 或查看matlab帮助
关于韦伯分布的一些了解知识参考链接
http://blog.sina.com.cn/s/blog_54c7e90e010005og.html
关于Beta分布的一些了解知识参考链接
https://www.zhihu.com/question/30269898
注:
Randperm和randsample的使用方法引用链接
http://blog.csdn.net/jiejinquanil/article/details/50057045的内容
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








