一、哈希
(一)两数之和

思路一:传统方法-双层循环遍历
时间复杂度:O(n^2)
空间复杂度:O(1)
class Solution {
public int[] twoSum(int[] nums, int target) {
// 两层循环求解 时间复杂度O(N^2) 空间复杂度O(1)
int[] goal = new int[2];
for (int i = 0; i < nums.length - 1; i++) {
for (int j = i+1; j < nums.length; j++) {
if ( (nums[i] + nums[j]) == target ) {
goal[0] = i;
goal[1] = j;
return goal;
}
}
}
throw new IllegalArgumentException("no such two nums.");
}
}
思路二:HashMap方法-一次遍历
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public int[] twoSum(int[] nums, int target) {
// HashMap求解 时间复杂度O(N) 空间复杂度O(N)
Map<Integer, Integer> numsMap = new HashMap();
numsMap.put(nums[0], 0);
for (int i = 1; i < nums.length; i++) {
// 计算当前值距离目标值的补数
int complement = target - nums[i];
// 查看当前补数是否存在numsMap中
if (numsMap.containsKey(complement)) {
return new int[] { numsMap.get(complement), i};
}
// 不存在,将当前值加入numsMap中
numsMap.put(nums[i], i);
}
throw new IllegalArgumentException("未找到符合要求的两个下标");
}
}
(二)字母异位词分组


思路:采用哈希+排序
时间复杂度:O(N*M log M) N为字符串数组长度,M为字符串长度
空间复杂度:O(N*M)
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
// 字母异位词分组
// 时间复杂度 O(N*MlogM) N为字符串数组长度,M为字符串长度
// 空间复杂度 O(N*M)
// 创建一个HashMap,键存储排序后的字符串,值存储字母异位词
Map<String, List<String>> anagramMap = new HashMap<>();
// 遍历字符串数组
for (String str : strs) {
// 对字符串重新进行排序
char[] chars = str.toCharArray();
Arrays.sort(chars);
String sortedStr = new String(chars);
// 如果哈希表不存在该字符串,则添加
if ( !anagramMap.containsKey(sortedStr) ) {
// 哈希表新增
anagramMap.put(sortedStr, new ArrayList<>());
}
// 哈希表value赋值
anagramMap.get(sortedStr).add(str);
}
return new ArrayList<>(anagramMap.values());
}
}
(三)最长连续序列

思路一:常规解法:数组排序;双层循环遍历,找出最大的length
时间复杂度为:O(N*logN) + O(N^2)
空间复杂度:O(1)
思路二:哈希解法 要去重->HashSet
时间复杂度:O(N)
空间复杂度:O(N)
class Solution {
public int longestConsecutive(int[] nums) {
// 哈希解法 要去重 -> HashSet 时间复杂度:O(N) 空间复杂度:O(N)
Set<Integer> numSet = new HashSet<>();
// 遍历nums,加入numSet
for (int num : nums) {
numSet.add(num);
}
// 最长序列长度
int longest = 0;
// 遍历numSet,查找最长连续序列
for (int num : numSet) {
// 仅当num-1不存在numSet中,才认定num是个最长序列的起点
if ( !numSet.contains(num - 1)) {
// 当前长度和当前currentNum
int length = 1;
int currentNum = num + 1;
// 查找numSet中currentNum的下一值
while ( numSet.contains(currentNum) ) {
length++;
currentNum++;
}
// 更新最长序列长度
longest = longest > length ? longest : length;
}
}
// 返回最长序列长度
return longest;
}
}
二、双指针
(一)移动零

思路:采用双指针法求解,i记录非零下标,j遍历数组nums,移动非零元素,j遍历完之后,i及之后的元素均为0。
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public void moveZeroes(int[] nums) {
// 双指针法求解 时间复杂度O(N) 空间复杂度O(1)
// i记录非零元素的下标
int i = 0;
// 遍历nums
for (int j = 0; j < nums.length; j++) {
if (nums[j] != 0) {
nums[i] = nums[j];
i++;
}
}
// >=i之后的元素设置为0
for (int j = i; j < nums.length; j++) {
nums[j] = 0;
}
}
}
(二)盛最多水的容器

思路一:常规解法,采用双层循环。
时间复杂度:O(N^2)
空间复杂度:O(1)
实现代码:
class Solution {
public int maxArea(int[] height) {
// 双层循环解法
// 时间复杂度 O(N^2)
// 空间复杂度 O(1)
// maxArea表示容器的最大水量
int maxArea = 0;
// 外层循环遍历height
for (int i = 0; i < height.length-1; i++) {
// 记录当前的容器水量
int currentArea = 0;
// 内层循环 寻找盛最多水的下标
for (int j = i+1; j < height.length; j++) {
// 容器长度:j - i
int length = j - i;
// 容器宽度:Math.min(height[i], height[j])
int width = height[i] > height[j] ? height[j] : height[i];
currentArea = length * width;
maxArea = maxArea > currentArea ? maxArea : currentArea;
}
}
// 返回容器的最大水量
return maxArea;
}
}
思路二:双指针法。
时间复杂度:O(N)
空间复杂度:O(1)
实现代码:
class Solution {
public int maxArea(int[] height) {
// 双指针解法 容器面积:(j - i) * (Math.min(height[i], height[j]))
// 时间复杂度:O(N)
// 空间复杂度:O(1)
int i = 0, j = height.length-1;
// 容器最大水量
int maxArea = 0;
// 寻找容器最大水量
while (i < j ) {
// 记录当前的容器水量
int currentArea = ( j - i ) * ( height[i] > height[j] ? height[j] : height[i] );
// 更新容器最大水量
maxArea = maxArea > currentArea ? maxArea : currentArea;
// 指针移动判断,谁小移动谁
if ( height[i] < height[j] ) {
i++;
} else {
j--;
}
}
// 返回容器的最大水量
return maxArea;
}
}
(三)三数之和

思路:排序+双指针解法;排序使得nums有序,后遍历nums数组,固定第一个数,采用双指针分别指向下一个数和数组最后一个数,逐个寻找和为0的目标数。
时间复杂度:O(N^2)
空间复杂度:O(1)
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
// 排序+双指针解法
// 时间复杂度:O(N*logN) + O(N^2) = O(N^2)
// 空间复杂度:O(1)
// 构建result数组
List<List<Integer>> result = new ArrayList<>();
// 对nums数组进行排序
Arrays.sort(nums);
// 遍历数组nums
for (int i = 0; i < nums.length-2; i++) {
// 跳过重复的元素
if (i > 0 && nums[i] == nums[i-1]) {
continue;
}
// 双指针left、right赋值
int left = i+1, right = nums.length-1;
// nums[i] + nums[left] + nums[right] == 0
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0) {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 跳过重复的元素
while (left < right && nums[left] == nums[left+1]) {
left++;
}
while (left < right && nums[right] == nums[right-1]) {
right--;
}
// 双指针更新
left++;
right--;
} else if (sum < 0) {
left++;
} else {
right--;
}
}
}
// 返回result
return result;
}
}
(四)接雨水

思路:双指针解法
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public int trap(int[] height) {
// 接雨水 双指针解法
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 左右指针
int left = 0, right = height.length-1;
// 左右最大高度
int leftMax = 0, rightMax = 0;
// 最大雨水量
int water = 0;
// 当左右指针不相逢时,遍历
while ( left < right ) {
// 当左边柱子小于右边柱子时,处理左边
if ( height[left] < height[right] ) {
// 若当前高度大于等于左边最大高度,更新leftMax
if ( height[left] >= leftMax ) {
leftMax = height[left];
} else {
// 否则,更新最大雨水量
water = water + (leftMax - height[left]);
}
left++;
} else {
// 当左边柱子大于等于右边柱子时,处理右边
// 若当前高度大于等于右边最大高度,更新rightMax
if ( height[right] >= rightMax ) {
rightMax = height[right];
} else {
// 否则,更新最大雨水量
water += rightMax - height[right];
}
right--;
}
}
// 返回总的接住的雨水量
return water;
}
}
二、滑动窗口
(一)无重复字符的最长子串

思路:滑动窗口解法(哈希集+双指针法)。
时间复杂度:O(N)
空间复杂度:O(N)
class Solution {
public int lengthOfLongestSubstring(String s) {
// 滑动窗口解法
// 时间复杂度:O(N)
// 空间复杂度:O(N)
// 使用哈希来存储最长子串
Set<Character> set = new HashSet<>();
// 初始化左右指针和最大长度
int left = 0, right = 0;
int maxLength = 0;
// 开始滑动窗口遍历字符串
while (right < s.length()) {
// 如果当前字符不在哈希集中,说明未重复,加入哈希集中,并右移右指针
if ( !set.contains(s.charAt(right)) ) {
set.add(s.charAt(right));
right++;
// 更新最大长度
maxLength = Math.max(maxLength, right - left);
} else {
// 移除当前重复的元素
set.remove(s.charAt(left));
// 左指针右移更新
left++;
}
}
// 返回记录的最大长度
return maxLength;
}
}
(二)找到字符串所有字母异位词子串

思路:滑动窗口解法(数组+双指针法)
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public List<Integer> findAnagrams(String s, String p) {
// 使用数组 + 双指针法求解
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 构建结果数组
List<Integer> result = new ArrayList<>();
// 处理特殊情况
if ( s.length() < p.length() ) {
return result;
}
// 构建pFreq数组,存储目标子串元素
int[] pFreq = new int[26];
for ( char c : p.toCharArray() ) {
pFreq[c - 'a']++;
}
// 构建sFreq数组,存储遍历子串元素
int[] sFreq = new int[26];
// 构建双指针及初始化
int left = 0, right = 0;
// 遍历字符串s
while (right < s.length() ) {
// 将当前元素加入sFreq数组中
sFreq[s.charAt(right) - 'a']++;
// 若当前子串长度和目标子串长度一致,判断是否为异位词
if ( (right-left+1) == p.length() ) {
if ( matches(sFreq, pFreq) ) {
result.add(left);
}
// 未命中,更新频率表,左指针右移
sFreq[s.charAt(left) - 'a']--;
left++;
}
// 若长度不一致,右指针右移
right++;
}
// 返回结果数组
return result;
}
// 私有函数,用来判断两个字符串是否相等
private Boolean matches(int[] sFreq, int[] pFreq) {
for (int i = 0; i < 26; i++ ) {
if ( sFreq[i] != pFreq[i] ) {
return false;
}
}
// 全部相等,返回true
return true;
}
}
三、子串
(一)和为K的子数组

思路:前缀和+哈希表解法
时间复杂度:O(N)
空间复杂度:O(N)
重要概念理解:

class Solution {
public int subarraySum(int[] nums, int k) {
// 和为K的子数组
// 思路:前缀和+哈希表解法
// 创建一个哈希表,存储前缀和,默认初始值[0:1],键存前缀和,值存出现次数
Map<Integer, Integer> prefixSumCount = new HashMap<>();
prefixSumCount.put(0, 1);
// 记录子串数量
int count = 0;
// 记录当前前缀和
int currentSum = 0;
// 遍历数组nums
for (int num : nums) {
// 计算当前前缀和,若currentSum - k的值存在哈希表中,则是符合要求的子串,更新子串数量,更新哈希表前缀和的值
currentSum += num;
if ( prefixSumCount.containsKey(currentSum-k) ){
count += prefixSumCount.get(currentSum-k);
}
prefixSumCount.put( currentSum, prefixSumCount.getOrDefault(currentSum, 0) + 1 );
}
// 返回子串数量
return count;
}
}
(二)滑动窗口最大值

思路:双端队列解法
时间复杂度:O(N)
空间复杂度:O(N)
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 滑动窗口最大值
// 时间复杂度O(N)
// 空间复杂度O(N)
// 处理异常情况
if (nums.length == 0 || nums == null || k <= 0) {
return new int[0];
}
// 结果数组
int[] result = new int[nums.length - k + 1];
// 使用双端队列存储索引
Deque<Integer> deque = new LinkedList<>();
// 遍历数组
for (int i = 0; i < nums.length; i++) {
// 1. 移除不在当前窗口范围内的元素
if (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
deque.pollFirst();
}
// 2. 移除队列中所有小于当前元素的索引
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
// 3. 将当前元素加入到双端队列中
deque.offerLast(i);
// 4. 将窗口大小达到k时,将当前窗口的最大值加入到结果数组中
if (i >= k-1) {
result[ i-k+1] = nums[deque.peekFirst()];
}
}
// 返回结果数组
return result;
}
}
四、普通数组
(一)最大子数组和

思路:动态规划法
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public int maxSubArray(int[] nums) {
// 最大子数组和
// 思路:动态规划
// 异常处理
if (nums == null || nums.length == 0) {
throw new IllegalArgumentException("Array cannot be empty.");
}
// 初始化动态规划变量
int currentMax = nums[0];
int globalMax = nums[0];
// 遍历数组nums
for (int i = 1; i < nums.length; i++) {
// 1. 更新局部子数组和
currentMax = Math.max(nums[i], currentMax+nums[i]);
// 2. 更新全局子数组和
globalMax = Math.max(currentMax, globalMax);
}
// 返回最大子数组和
return globalMax;
}
}
(二)合并区间

思路:排序+合并
时间复杂度:O(NlogN)
空间复杂度:O(N)
class Solution {
public int[][] merge(int[][] intervals) {
// 思路:排序+合并区间
// 时间复杂度:0(NlogN)
// 空间复杂度:O(N)
// 异常情况处理
if (intervals == null || intervals.length == 0) {
return new int[0][0];
}
// 对区间按起始位置进行排序
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
// 定义合并后的区间
List<int[]> merged = new ArrayList<>();
// 遍历排序后的区间列表
for (int i = 0; i < intervals.length; i++) {
int[] currentInterval = intervals[i];
// 1. 如果结果列表为空,或者当前区间与结果列表中最后一个区间不重叠,直接添加当前区间
if (merged.isEmpty() || merged.get(merged.size() - 1)[1] < currentInterval[0]) {
merged.add(currentInterval);
} else {
// 2. 合并区间,更新结果列表中最后一个区间的结束位置
int[] lastMerged = merged.get(merged.size()-1);
lastMerged[1] = Math.max(lastMerged[1], currentInterval[1]);
}
}
// 将结果转换成二维数组返回
return merged.toArray(new int[merged.size()][]);
}
}
(三)轮转数组

思路:三次轮转法,第一次将数组反转,第二次将前k个元素轮转,第三次将剩余元素轮转。
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public void rotate(int[] nums, int k) {
// 轮转数组
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 如果数组为空或数组只有一个元素,或者k为0,无需轮转
if (nums == null || nums.length <= 1 || k == 0) {
return;
}
// 获取数组长度
int n = nums.length;
// 如果k大于数组长度,取模以减少不必要的轮转
k = k % n;
// 使用三次轮转法实现轮转
// 第一次反转整个数组
reverse(nums, 0, n-1);
// 第二次反转前k个元素
reverse(nums, 0, k-1);
// 第三次反转剩余元素
reverse(nums, k, n-1);
}
// 反转函数
private void reverse(int[] nums, int start, int end) {
while (start < end) {
// 交换元素
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
// 缩小范围继续交换
start++;
end--;
}
}
}
(四)除自身以外数组的乘积
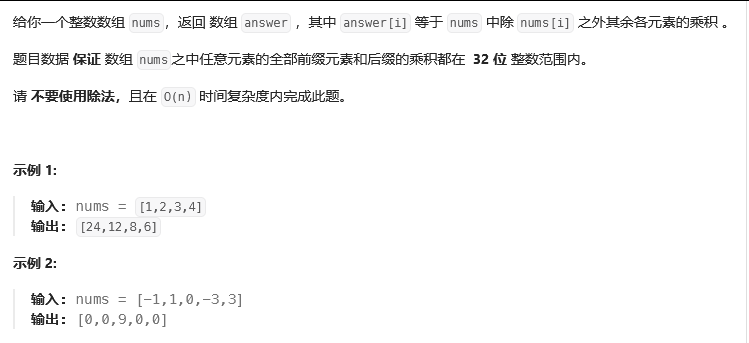
思路:前缀乘积+后缀乘积
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public int[] productExceptSelf(int[] nums) {
// 前缀乘积+后缀乘积解法
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 数组长度
int n = nums.length;
// 定义答案数组
int[] answer = new int[n];
// 计算前缀乘积
// 前缀乘积初始化首元素为1
answer[0] = 1;
// 前缀乘积赋值
for (int i = 1; i < n; i++) {
answer[i] = answer[i-1] * nums[i-1];
}
// 计算后缀乘积
// 后缀乘积初始化suffix= 1
int suffix = 1;
// 更新答案数组的当前元素:前缀乘积*后缀乘积
for (int i = n-1; i >= 0; i--) {
answer[i] = answer[i] * suffix;
// 更新后缀乘积
suffix *= nums[i];
}
// 返回答案数组
return answer;
}
}
(五)缺失的第一个正数

思路:
第一步:预处理数组,去掉干扰数
为了能更方便地利用数组来记录哪些正整数出现过,咱们先把数组过一遍,把所有小于等于 0 的数,都改成 “数组长度 + 1” 。为啥要这么干呢?因为我们只关心在 “1 到数组长度” 这个范围内的正整数,那些小于等于 0 的数,对找缺失的最小正整数没帮助,还会捣乱,所以先把它们处理掉。处理之后,除了那些本来小于等于 0 (现在被改成 “数组长度 + 1” ) 的数,数组里其他数都是正数,后续操作就更方便统一啦。
第二步:借助数组下标和值的关系做标记(类似在小本本上记录)
接下来,再把数组从头到尾看一遍。对于看到的每一个数 x,因为之前有些数被改过,所以先取它的绝对值,得到原来对应的数。
要是这个绝对值在 “1 到数组长度” 范围内,就说明这个数是我们要找的有效范围内的正整数。这时候,就给数组里第 “绝对值 - 1” 个位置的数添个负号 (数组下标是从 0 开始数的,所以要减 1),就像在小本本上打个勾,标记这个正整数已经出现过。要是这个位置的数已经是负数了,说明之前已经标记过这个正整数了,就不用再重复标记了。
第三步:根据标记结果,找出缺失的最小正整数
经过前面两步,数组里数的正负情况,就代表了对应的下标值(当作正整数看)有没有出现过。
最后,再把数组过一遍,从下标 0 开始找。要是发现某个位置 i 上的数是正数,那就说明 “i+1” 这个正整数没在数组里出现过(因为按照之前的标记方法,出现过的正整数,对应的位置应该是负数),那 “i+1” 就是咱们要找的缺失的最小正整数。
要是把整个数组看完,发现所有的数都是负数,那就说明从 1 到 “数组长度” 的所有正整数,都在数组里出现过了。按照一开始确定的范围,这时候缺失的最小正整数就是 “数组长度 + 1” 。
时间复杂度:O(N)
空间复杂度:O(1)
class Solution {
public int firstMissingPositive(int[] nums) {
// 缺失的第一个正数
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 获取数组长度
int n = nums.length;
// 第一步,处理不合法的元素(<=0 || >n)
for (int i = 0; i < n; i++) {
if (nums[i] <=0 || nums[i] > n) {
nums[i] = n+1;
}
}
// 第二步,使用原地哈希方法标记已经出现的正整数
for (int i = 0; i < n; i++) {
int num = Math.abs(nums[i]);
if (num <= n) {
// 出现的正数,全部标记为负数
if (nums[num-1] > 0) {
nums[num-1] = -nums[num-1];
}
}
}
// 第三步,查找第一个未出现的正整数
for (int i = 0; i < n; i++) {
if (nums[i] > 0) {
return i+1;
}
}
// 如果所有位置都被标记,返回n+1
return n+1;
}
}
五、矩阵
(一)矩阵置零
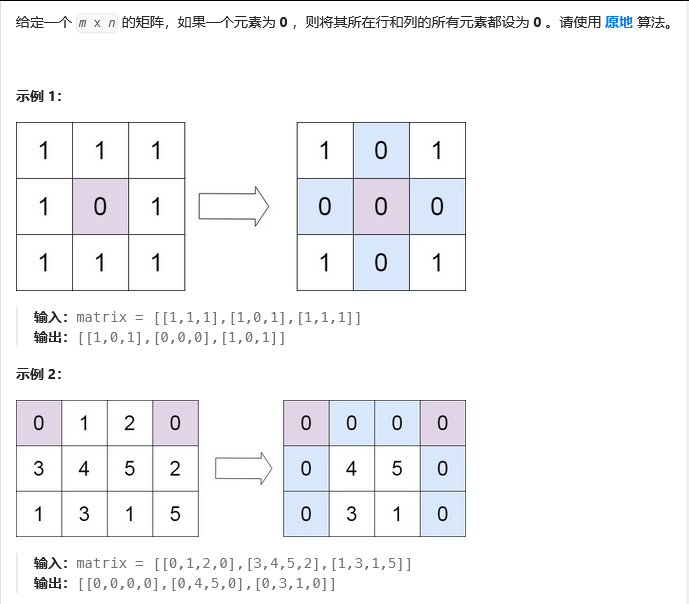
思路:
第一步,记录第一行和第一列含0情况;
第二步,遍历矩阵(除首行首列),若含0则行首列首置0;
第三步,遍历矩阵,行首列首含0则整行整列置0;
第四步,根据记录首行首列0情况进行置0处理。
时间复杂度:O(M*N)
空间复杂度:O(1)
class Solution {
public void setZeroes(int[][] matrix) {
// 获取矩阵的行数和列数
int row = matrix.length;
int col = matrix[0].length;
// 记录第一行和第一列含0情况
boolean rowWithZero = false;
boolean colWithZero = false;
for (int j = 0; j < col; j++) {
if (matrix[0][j] == 0) {
rowWithZero = true;
break;
}
}
for (int i = 0; i < row; i++) {
if (matrix[i][0] == 0) {
colWithZero = true;
break;
}
}
// 遍历矩阵(除首行首列),若含0则行首列首置0
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
// 遍历矩阵,行首列首含0则整行整列置0
// - 处理行
for (int i = 1; i < row; i++ ) {
if (matrix[i][0] == 0) {
for (int j=1; j < col; j++ ) {
matrix[i][j] = 0;
}
}
}
// - 处理列
for (int j = 1; j < col; j++ ) {
if (matrix[0][j] == 0) {
for (int i = 1; i < row; i++ ) {
matrix[i][j] = 0;
}
}
}
// 根据记录首行首列0情况进行置0处理
if (rowWithZero) {
for (int j = 0; j < col; j++ ) {
matrix[0][j] = 0;
}
}
if (colWithZero) {
for (int i = 0; i < row; i++ ) {
matrix[i][0] = 0;
}
}
}
}
(二)螺旋矩阵
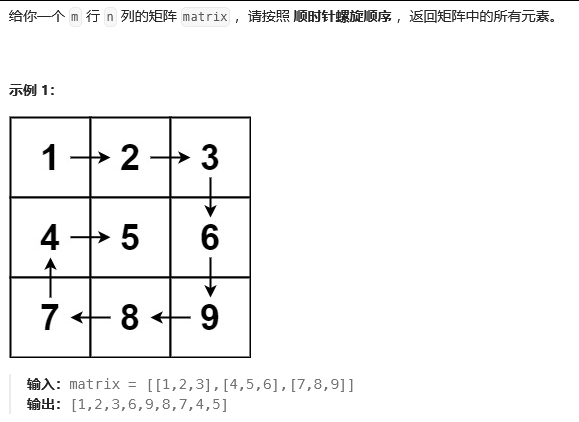
思路:
第一步,初始化边界。
第二步,遍历各边界。
- 从左到右遍历上边界
- 从上到下遍历右边界
- 从右到左遍历下边界
- 从下到上遍历上边界
时间复杂度:O(M*N)
空间复杂度:O(M*N)
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
// 定义结果数组
List<Integer> result = new ArrayList<>();
// 获取矩阵的行数和列数
int row = matrix.length;
int col = matrix[0].length;
// 初始化边界值
int top = 0, bottom = row-1;
int left = 0, right = col-1;
// 遍历各边界
while (top <= bottom && left <= right) {
// 从左到右遍历上边界
for (int j = left; j <= right; j++) {
result.add(matrix[top][j]);
}
// 上边界向下移动
top++;
// 从上到下遍历右边界
for (int i = top; i <= bottom; i++) {
result.add(matrix[i][right]);
}
// 右边界从左移动
right--;
// 避免重复遍历,需进行判断
if (top <= bottom) {
// 从右到左遍历下边界
for (int j = right; j >= left; j--) {
result.add(matrix[bottom][j]);
}
// 下边界向上移动
bottom--;
}
// 避免重复遍历,需进行判断
if (left <= right) {
// 从下到上遍历左边界
for (int i = bottom; i >= top; i--) {
result.add(matrix[i][left]);
}
// 左边界向右移动
left++;
}
}
// 返回结果数组
return result;
}
}
(三)旋转图像
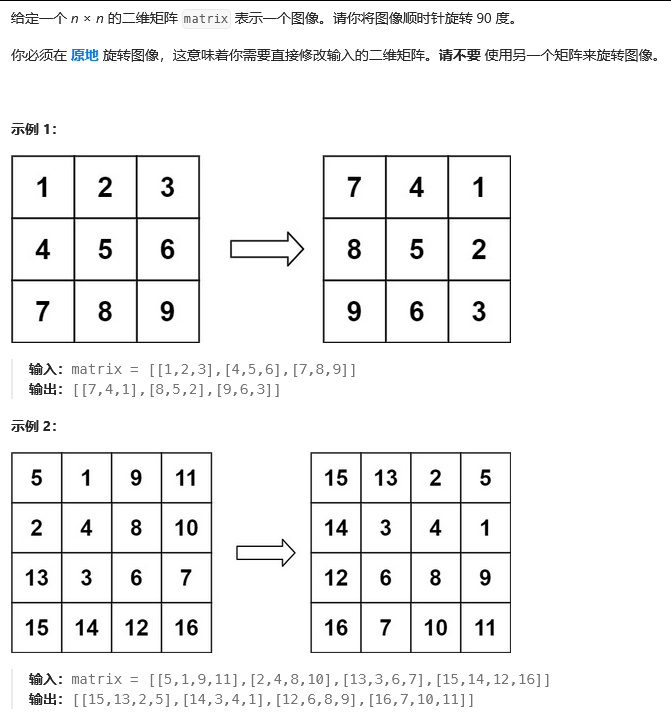
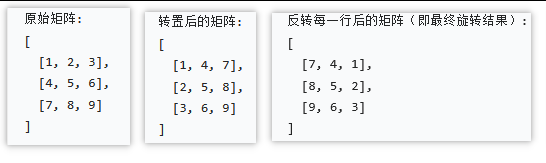
思路:顺时针旋转图像90°,相当于对矩阵进行转置,然后再对每一行进行反转。
时间复杂度:O(N^2)
空间复杂度:O(1)
class Solution {
public void rotate(int[][] matrix) {
// 获取矩阵的行数
int n = matrix.length;
// 矩阵转置(仅需要处理上三角即可,避免重复)
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// 三步交换
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 矩阵反转
for (int i = 0; i < n; i++) {
int left = 0;
int right = n-1;
while (left < right) {
// 三步交换
int temp = matrix[i][left];
matrix[i][left] = matrix[i][right];
matrix[i][right] = temp;
// 左右指针移动
left++;
right--;
}
}
}
}
(四)搜索二维矩阵II
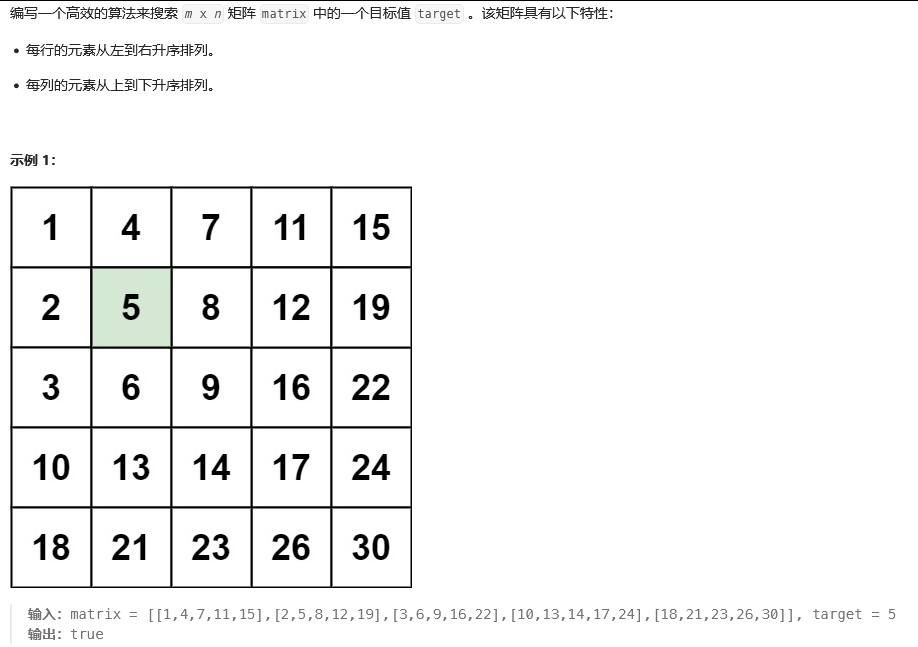
思路:由于此二维矩阵有序,即行升序,列也升序。可以选择从右上角出发,若目标值小于左上角,左移查找;若目标值大于右上角,下移查找。循环往复,直至目标或者移至边界(未找到)。
时间复杂度:O(M+N)
空间复杂度:O(1)
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
// 获取矩阵行数和列数
int m = matrix.length;
int n = matrix[0].length;
// 左上角坐标
int row = 0;
int col = n-1;
// 寻找目标值
while (row < m && col >= 0) {
if (matrix[row][col] == target) {
return true;
} else if (target > matrix[row][col]) {
row++;
} else {
col--;
}
}
// 返回查找结果
return false;
}
}
六、链表
(一)相交链表
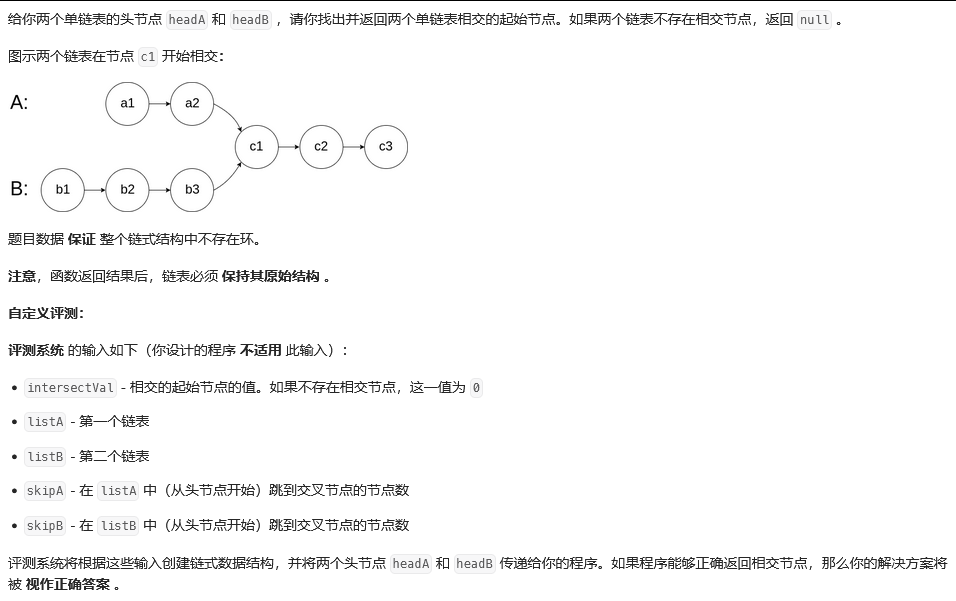

思路:假设链表A的长度为m,链表B的长度为n,他们相交的长度为c;通过指针pA遍历完A再遍历B,所经历的长度为m+n;指针pB同理,长度为n+m;通过同时移动,到达相交点时,他们的相交长度均为c。
时间复杂度:O(m+n)
空间复杂度:O(1)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 若链表A或B存在null,则直接返回null
if (headA == null || headB == null) {
return null;
}
// 初始化两个指针
ListNode pA = headA;
ListNode pB = headB;
// 当两个指针不相等时继续遍历
while (pA != pB) {
// 遇到链表末尾时,切换到另一链表
pA = (pA == null) ? headB : pA.next;
pB = (pB == null) ? headA : pB.next;
}
// 返回相交的节点或者null
return pA;
}
}
(二)反转链表
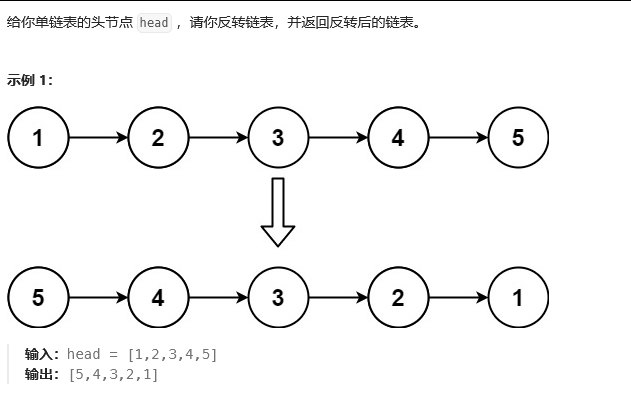
思路一:迭代方法
- 使用三个指针来反转链表:pre(前一节点),cur(当前节点),next(下一节点)
- 遍历链表,将当前节点的next指针指向前一个节点,更新pre和cur指针,直到遍历完成
时间复杂度:O(N)
空间复杂度:O(1)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
// 迭代方法,定义三个指针:pre,cur,next
// 时间复杂度:O(N)
// 空间复杂度:O(1)
ListNode pre = null;
ListNode cur = head;
// 若当前指针不为空,则遍历
while (cur != null) {
// 保存下一个节点
ListNode next = cur.next;
// 反转当前节点的指针
cur.next = pre;
// 更新前一个节点
pre = cur;
// 移动到下一节点
cur = next;
}
// 返回新头节点
return pre;
}
}
思路二:递归方法
- 递归处理链表的尾部,并将每个节点的next指针指向当前节点,从而实现反转。
- 基本的递归策略是:反转链表的其余部分,然后将当前节点追加到反转链表的尾部。
时间复杂度:O(N)
空间复杂度:O(N)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
// 递归方法
// 时间复杂度:O(N)
// 空间复杂度:O(N) 注:递归调栈
// 链表为空或者只有一个节点
if (head == null || head.next == null) {
return head;
}
// 递归反转链表的剩余部分
ListNode newHead = reverseList(head.next);
// 反转当前节点和更新下一节点
head.next.next = head;
head.next = null;
// 返回新头节点
return newHead;
}
}
(三)回文链表
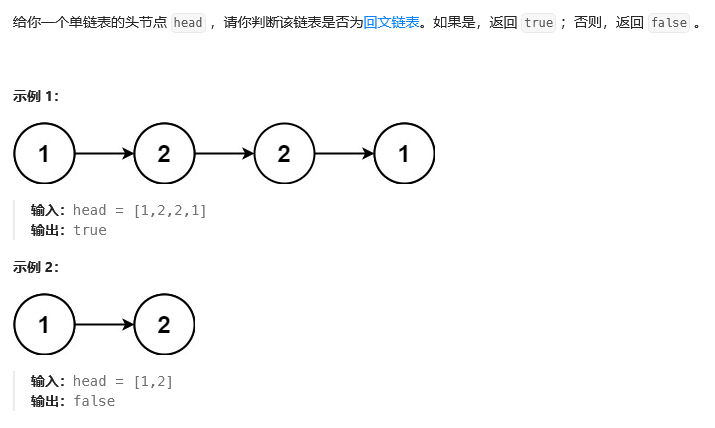
思路:
- 链表仅有一个元素或空情况
- 通过快慢指针查找中间节点
- 反转链表后半部分
- 比较链表前半部分和后半部分
- 恢复链表原始状态
时间复杂度:O(N)
空间复杂度:O(1)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
// 链表仅有一个元素或空情况
if (head == null || head.next == null) {
return true;
}
// 通过快慢指针查找中间节点
ListNode slow = head;
ListNode fast = head;
while ( fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 反转链表后半部分
ListNode secondHalf = reverseList(slow);
ListNode firstHalf = head;
// 比较链表前半部分和后半部分
while (secondHalf != null) {
if (firstHalf.val != secondHalf.val) {
return false;
}
firstHalf = firstHalf.next;
secondHalf = secondHalf.next;
}
// 恢复链表原始状态
ListNode MidNode = reverseList(slow);
return true;
}
// 反转链表
private ListNode reverseList(ListNode head) {
// 定义pre/cur/next指针
ListNode pre = null;
ListNode cur = head;
// 链表不为空,遍历
while (cur != null) {
// 保存下一节点
ListNode next = cur.next;
// 反转链表节点
cur.next = pre;
// 更新pre节点
pre = cur;
// 更新当前节点
cur = next;
}
// 返回头节点
return pre;
}
}
(四)环形连接
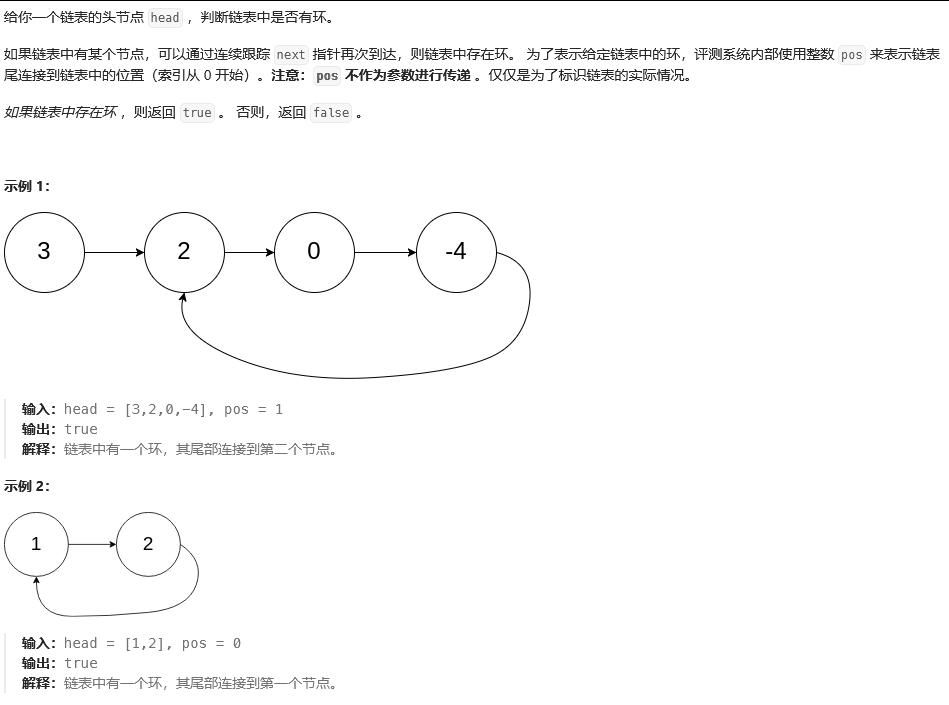
思路:快慢指针法求解
时间复杂度:O(N)
空间复杂度:O(1)
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
// 龟兔算法/快慢指针法求解
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 指针为空/指针仅有一个节点
if (head == null || head.next == null) {
return false;
}
// 初始化快慢指针
ListNode slow = head;
ListNode fast = head;
// 循环遍历
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
// 快慢指针相遇,则表示链表中有环
if (slow == fast) {
return true;
}
}
// 链表无环,返回false
return false;
}
}
七、贪心算法

贪心算法:在每一步选择中都采取当前状态下最优的选择,达到局部最优解,期盼最终结果就是全局最优解。
class Solution {
public int maxProfit(int[] prices) {
// 时间复杂度:O(N)
// 空间复杂度:O(1)
// 初始化最小价格为正无穷
int minPrice = Integer.MAX_VALUE;
// 初始化最大利润为0
int maxProfit = 0;
// 遍历每一天的gp价格
for (int price : prices) {
// 若当前价格小于最小价格,则更新最小价格
if (price < minPrice) {
minPrice = price;
} else if (price - minPrice > 0) {
// 否则计算最大利润
// maxProfit = (price - minPrice) > maxProfit ? (price - minPrice) : maxProfit;
}
}
// 返回最大利润
return maxProfit;
}
}





















 1810
1810

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








