操作系统学习笔记——2.1内存调度算法

内存调度算法

**功能目标：**当缺页中断发生，需要调入新的页面而内存已经满了，选择内存当中哪个物理页面被置换

**目标：**尽量减少页面中断的次数。具体来说，把未来不在使用的或短期内较少使用的页面换出，通常只能在局部性原理指导下依据过去的统计数据来进行预测。

要知道并不是所有物理页都需要换进换出，那么这些就是常驻内存，比如放在操作系统中的某些代码段、数据， 这里就要用到页面锁定：用于描述必须常驻内存的操作系统的关键部分或时间关键的应用程序。实现方法是：在页表中添加锁定标志位。

1、最优页面置换算法

基本思路：置换在未来最长时间不访问的页面

举个例子，有三个空闲的物理页，然后有请求的页面序列，具体的流程如下图

缺页共发生了七次（空闲页三次+最优页面置换四次）

2、先进先出算法FIFO

基本思路：选择在内存中驻留时间最长的页面并淘汰之。

具体来说系统维护一个链表，记录了所有位于内存当中的逻辑页面。从链表的排序来看，链首页面的驻留时间最长，链尾驻留时间最短。当发生一个缺页中断时，把链首页面淘汰出局，并把新的页面添加到链表的末尾。

例子还是和最优的类似模型

发生了十次缺页，页面置换发生了七次

明显性能较差，调出的页面可能时常用的页面，并且有Belady现象，很少单独使用。

3、最近最久页面置换算法（Least Recently Used,LRU）

基本思路：当缺页发生时，选择最久未使用的那个页面并淘汰。

也就是说，该算法假设已经很久没有使用的页面很有可能在未来较长的一段时间不会被使用。

这种方法和最优置换方法类似，但是最优置换算法是通过未来的使用情况来推测要淘汰的，最近最久置换算法是通过历史的使用情况来推测要淘汰的。

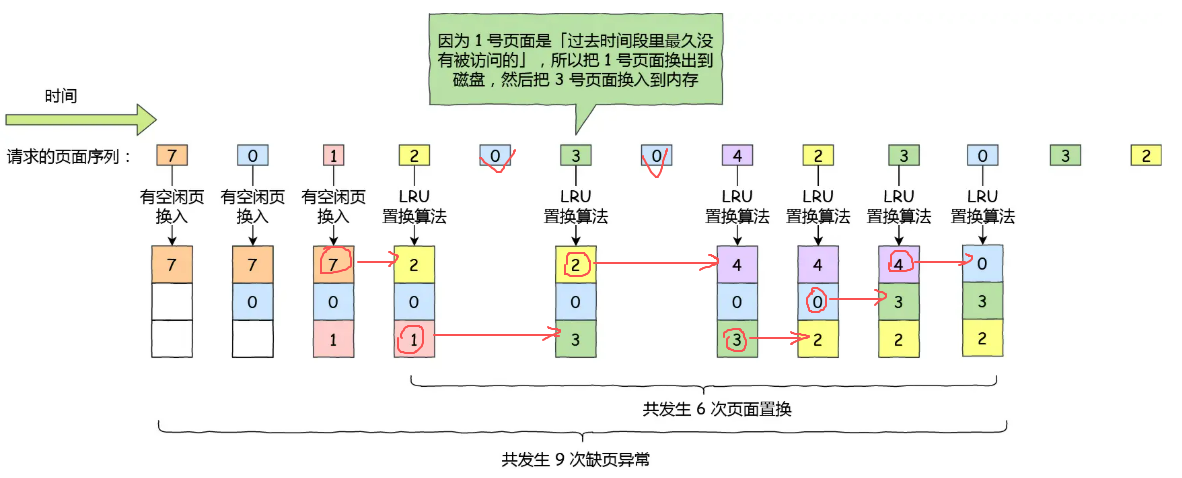
缺页异常发生了九次，发生六次页面置换，性能相比先进先出算法会更高一些。

LRU在理论上可以实现，但是代价很高。

两种可能实现的方法：

●需要在内存中维护一个所有页面的链表，最近刚刚使用过的页面作为首结点，最久未使用的页面作为尾节点。每次访问内存时，找到相应的页面，把它从链表中摘下再放到链首。每次缺页发生中断时，淘汰链表末尾的页面。

●设置一个活动页面栈。当访问某页时，将此页号压入栈底，然后考察栈内是否有一样的页号，若有则抽出，当要淘汰一个页面时，栈底就是最久未使用的页面。

困难的是每次访问内存时都要更新整个链表。在链表中找到一个页面，删除它，然后把它移动到表头是一个费时的操作。

所以LRU看上去不错，但是开销很大，在实际中的应用也很少。

4.时钟页面置换算法

与LRU的近似，对FIFO的一种改进

基本思路：

• 需要用到页表项中的访问位，页面存入内存时的初始状态是0，页面被访问了就被硬件置为1。

• 把各页面组织成环形链表，把指针指向最老的页面（最先进来）

• 当发生一个缺页中断时，考察指针所指向的最老页面。若它的访问位是0，立即淘汰；若访问位位1，则把该位置为0，然后指针跳到下一格。重复这个过程。

简单示例

使用位标志这个页面最近是否被访问过，访问过就置为1，当指针在环形链表中开始逐个查找，当访问到page0，该位当前是1则置为0，让它老一点，并且指针移到下一个位置，一直找到访问位为0的页表项则淘汰，替换为需要插入的页表。

5.二次机会法

增加一个dirty 位（脏位），并由硬件完成置位。修改clock算法，同时使用脏位和使用位来指导置换。

如果是写操作，把dirty bit和used bit都置为1；如果是读操作，used bit是1，dirty bit是0。

通过dirty bit指导我们对硬盘的访问，即写回的次数。

6.最不常用法(Least Frequently Used,LFU)

基本思路：当一个缺页中断发生时，选择访问次数最少的那个页面，并淘汰之。

实现方法：对每个页面设置一个访问器，每当一个页面被访问时，该页面的访问计数器加1。发生缺页中断时，淘汰计数最小的那个页面。

在操作系统实际中实现时，要考虑效率还有硬件的成本（硬件的内存、计算器等）

LFU和LRU的区别：LRU考察的是多久未访问，时间越短越好；而LFU考察的是访问的次数或频度，访问次数越多越好

• 但还有个问题，LFU算法只考虑到了频率问题，没有考虑到时间问题，比如有些页面在过去时间里访问次数很高，但现在没有访问了，但是当前访问的页面没有这些页面访问的次数高，在发生缺页中断时，就会误伤当前才开始访问，并且次数不高的页面。

U算法只考虑到了频率问题，没有考虑到时间问题，比如有些页面在过去时间里访问次数很高，但现在没有访问了，但是当前访问的页面没有这些页面访问的次数高，在发生缺页中断时，就会误伤当前才开始访问，并且次数不高的页面。

• 这个问题的解决办法也是有的，可以定期减少访问的次数，当发生缺页中断时，所有的计数器就除以2，这样随着时间流失，以前访问次数高的就会越来越少，相当于加大了置换概率