分类型数据汇总:

- 频数:表示在几个互不重叠组别中的每一组项目的个数
- 相对频数:组的相对频数 = 组频数/n
- 百分数频数:组的百分数频数 = 组的相对频数 * 100%
数量型数据汇总:

- 数据型数据确定频率分布的步骤:
- 确定互不重叠的组数
- 确定每组的组宽
- 近似组宽 = (最大的数据值- 最小的数据值)/ 组数
- 确定组限
- 下组限、上组限、组中值

- 累计频数:表示小于或等于每一个组上组限的数据项个数
图形法:
- 散点图:两个变量的数据汇总
- 箱型图:基于五数概括法的汇总
- 最小值、第一四分位数(Q1)、中位数、第三四分位数(Q3)、最大值
数值法:
-
平均数:

-
中位数:
- 奇数:中间数值
- 偶数:中间两数值的平均数
-
众数:出现频率最高的数值
-
四分位数:
- 将n个数从小到大排列:
- Q2为n个数组成的数列的中数(Median);
- 当n为奇数时,中数Q2将该数列分为数量相等的两组数,每组有 (n-1)/2 个数,Q1为第一组 (n-1)/2 个数的中数,Q3为为第二组(n-1)/2个数的中数;
- 当n为偶数时,中数Q2将该数列分为数量相等的两组数,每组有n/2数,Q1为第一组 n/2个数的中数,Q3为为第二组 n/2 个数的中数。
-
加权平均数——案例
求:美国人和日本人的平均身高 已知:美国人平均身高,日本人平均身高 美国人口:3亿,日本人口:1亿 解:加权平均数=(美国人平均身高x3+日本人平均身高x1)/(1+3) -
变异程度的度量
-
极差:极差 = 最大值 = 最小值
-
四分位数间距:IQR = Q3 - Q1(第三分位数 - 第一 分位数)
-
方差
-
总体方差:

-
样本方差:

-
-
标准差:
-
总体标准差:

-
样本标准差:

-
标准差稀疏:

-
-
-
形态的度量
- 分布形态:偏度
- 对称分布:平均数与中位数相等
- 偏度为正值:平均数大于中位数
- 偏度为负值:平均数小于中位数
- 分布形态:偏度
-
相对位置的度量:
z分数(z-score),也叫标准分数(standard score)是一个数与平均数的差再除以标准差的过程
-
切比雪夫定理:
-
适用于任何数据集,不论其分布形态
-
与平均数的距离在z个标准差之内的数据项多占比例至少为(1-1/z**2),其中z是大于1的实数
- 至少有75%的数据与平均数的距离在z=2个标准差之内
- 至少有89%的数据与平均数的距离在z=3个标准差之内
- 至少有94%的数据与平均数的距离在z=4个标准差之内
切比雪夫例子:
例:切比雪夫定理 已知:某高中有100名学生,平均成绩为70分,标准差为5分 求:有多少学生的成绩在60-80之间?58-82之间? 解:60-80之间 60比平均数70小2个标准差;80比平均数70大两个标准差 利用切比雪夫定理,我们知道75%的学生考试成绩在60-80之间 58-82之间 z-分数:(58-70)/5=-2.4;(82-70)/5=+2.4 利用切比雪夫定理,(1-1/2.4**2)=0.826,我们知道82.6%的学生考试成绩在58-82之间
-
-
异常值的检验
- 方法一
- 利用标准化数值(z-分数)确认异常值
- 把z-分数小于-3或大于+3的数值视为异常值
- 方法二
- 利用Q1,Q3和IQR计算上限、下限确认异常值
- 下限=Q1 - 1.5 * IQR
- 上限=Q3 + 1.5 * IQR

- 方法一
-
两变量间关系的度量
-
协方差:

-
协方差的解释:
- 第1,2,3,4象限
- 当协方差为正:x和y之间存在正的线性关系
- 当协方差为负:x和y之间存在负的线性关系
- 当协方差接近零:x和y之间无线性关系
-
相关系数计算(皮尔逊积炬)
- 计算样本标准差,x1,y1
- 样本相关系数 :数量 / 标准差(x1 * y1)
- 样本相关系数的解释:
- 当系数为+1时:x和y之间存在完全正线性关系
- 当系数为-1时:x和y之间存在完全负线性关系
- 当系数接近0时:x和y之间存在弱线性关系
- 当系数为0时:x和y之间不存在线性关系
- 样本相关系数的解释:
-
样本相关系数的解释:
- 当系数为+1时:x和y之间存在完全正线性关系
- 当系数为-1时:x和y之间存在完全负线性关系
- 当系数接近0时:x和y之间存在弱线性关系
- 当系数为0时:x和y之间不存在线性关系








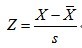
















 2026
2026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








