因为两周前,对继续读理论书有点抗拒,所以想找点可以直接动手做的事,后来就找到了LeetCode。
到目前在LeetCode上完成了前9道题。
比较考脑子,就算把功能完成了,但随后LeetCode显示的排名也会让你想继续想如何优化已经写好的代码,往往优化的结果就是把代码又重新实现了一次,比较费时间,但还好比较有意思。
LeetCode的题有些我是用JAVA实现,有些是用C#实现的。
1.Two Sum

这道题我最开始的实现很简单,直接两个for循环加一个判断就能实现了。
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length; i++)
{
//// find two numbers such that they ....
for (int j = i + 1; j < nums.length; j++)
{
if (nums[i] + nums[j] == target)
{
if (i < j)
{
//// your returned answers (both index1 and index2) are not zero-based.
return new int[] { i + 1, j + 1 };
}
else
{
return new int[] { j + 1, i + 1 };
}
}
}
}
//// targe not found
return new int[] { 0, 0 };
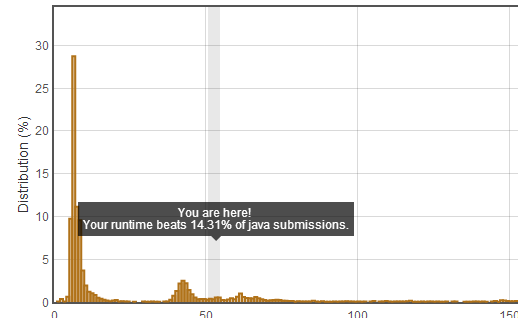
}一次跑通,但最后的跑分结果:
所以换了一个实现方式。把两个for循环的遍历换成了字典保存nums[]的所有成员。
我们要做的是每次在字典里查询是否主键为target-nums[i]。
import java.util.Hashtable;
import java.util.Map;
public class Solution {
private Map<Integer, Integer> hashTable = new Hashtable<Integer, Integer>();
public int[] twoSum(int[] nums, int target) {
for(int i = 0; i < nums.length; i++)
{
hashTable.put(nums[i], i);
}
Integer index = new Integer(0);
int indexInt = 0;
for(int i = 0; i < nums.length; i++)
{
index = hashTable.get(new Integer(target - nums[i]));
if(index != null && (int)index != i)
{
indexInt = (int)index;
if(i > indexInt)
{
i ^= indexInt;
indexInt ^= i;
i ^= indexInt;
}
return new int[]{i + 1, indexInt + 1};
}
}
return new int[]{0, 0};
}
}这样实现后跑分为40%,但还是不够,后面再改进吧。
2.Add Two Numbers
这道题一开始我就审错题了。
由此带来的结果是写完的代码对不上题目想要的逻辑。
又出现短节了。
事后好好想了下思维上出现的问题。
当A,B是遵循了The digits are stored in reverse orde。那么结果也该遵循这个规则。同一种类型应该是遵循一种规则的,为什么我会把AB和C分割开来思考,他们本该是一条线的,是不是我又想当然了,思维又开始到处跳跃了。
这道题需要处理的是进位。
跑分90%。
/**
* Definition for singly-linked list.
* public class ListNode {
* public int val;
* public ListNode next;
* public ListNode(int x) { val = x; }
* }
*/
public class Solution {
public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {
return this.Calc(l1, l2, 0);
}
private ListNode Calc(ListNode l1, ListNode l2, int carry)
{
if (l1 == null && l2 == null)
{
return carry == 0 ? null : new ListNode(1);
}
if (l1 == null)
{
l1 = new ListNode(0);
}
if (l2 == null)
{
l2 = new ListNode(0);
}
int sum = l1.val + l2.val + carry;
ListNode head = new ListNode(sum % 10);
head.next = Calc(l1.next, l2.next, sum / 10);
return head;
}
}3.Longest Substring Without Repeating Characters
这道题的解决思路类似前后两个指针prve,next,最开始prve,next都指向字符串第一个字符,然后每次next都移向下一个字符,而prev只在next所指向字符和prve指向字符相同时才后移,通过判断next和prev之间的长度就可以得到最大未重复子串。
现在的问题是如何保存上次字符出现的位置。思路类似第一题里的字典,但这里,我们可以用数组来描述这个hash表,由于题目中可以出现的字符没有做限制,那么我们可以按照ASCII码与每一个字符位置对应,作为数组的索引,数组中的内容就是出现这个字符出现的位置。
跑分90%。
public int lengthOfLongestSubstring(String s) {
上次出现的位置
int[] exist = new int[256];
int index = 0;
int maxLength = 0;
char[] arr = s.toCharArray();
for(int i = 0; i < arr.length; i++)
{
if(exist[arr[i]] > index)
{
index = arr[i] + 1;
}
if(i - index > maxLength)
{
maxLength = i - index;
}
exist[arr[i]] = i;
}
加上最后一次计算最大长度后再首次加入的字符数
return maxLength;
}4.Median of Two Sorted Arrays

这道题的实现,我绕了几个弯,要想办法用上两个子数组都是已排序的条件,这样的话用归并排序很有优势,但又要求是O(log(m+n))的时间复杂度,于是我用BST实现了整个排序,然后判断奇偶求出中位数,但这样的话我没有用上两个数组已排序的前提条件,把两个数组都重新排了次序,这样就浪费这个前提条件,查了下资料,很多实现都把这道题纳入了求Kth值得范围。如这里求两个有序数组的第k大值。两者本质上是一样的。
对于其实现,虽然跑出了结果,但我感觉还是没吃透。
跑分40%,还要改进。
private double findKth(int A[], int aBeg, int B[], int bBeg, int k)
{
if (A.length - aBeg < B.length - bBeg)
return findKth(B, bBeg, A, aBeg, k);
if (bBeg == B.length)
return A[aBeg + k - 1];
if (k == 1)
return Math.min(A[aBeg], B[bBeg]);
int pb = Math.min(k / 2, B.length - bBeg), pa = k - pb;
if (A[aBeg + pa - 1] > B[bBeg + pb - 1])
return findKth(A, aBeg, B, bBeg + pb, pa);
else if (A[aBeg + pa - 1] < B[bBeg + pb - 1])
return findKth(A, aBeg + pa, B, bBeg, pb);
else
return A[aBeg + pa - 1];
}
public double findMedianSortedArrays(int A[], int B[])
{
return (findKth(A, 0, B, 0, (A.length + B.length + 1) / 2) + findKth(A, 0, B, 0, (A.length + B.length + 2) / 2)) / 2.0;
} 5.Longest Palindromic Substring

这道题和第3题类似,只是那道题是找不重复,这里是要找重复,思路是对于第i个字符,检查i前一个和i后一个字符是否相等,相等则继续扩张。
但这里要区分abba和aba的情况。这样的话一个指针就没法解决这个问题了,那么如果是两个指针的话,i和j,比较i+1和j-1字符是否相等,这样虽然还是会遇到只有一个指针时要遇到的情况,但却不会错过abba的情况了。
保存是否两个位置上的字符是否相等,仍可以用数组来完成,第i个字符和第j个字符对于二维数组ij。用布尔类型来描述是否相等。
虽然实现了,但是最后的跑分,惨不忍睹。代码里的打标记过程就花费了n^2的复杂度。
public String longestPalindrome(String s) {
char[] arr = s.toCharArray();
boolean[][] flag = new boolean[arr.length][arr.length];
int maxLength = 0;
int index = 0;
for(int i = 0; i < arr.length; i++)
{
for(int j = 0; j < arr.length; j++)
{
if(arr[i] == arr[j])
{
flag[i][j] = true;
}
}
}
for(int j = 1; j < arr.length; j++)
{
for(int i = 0; i < j; i++)
{
if(arr[i] == arr[j] && flag[i + 1][j - 1])
{
if(j - i > maxLength)
{
index = i;
maxLength = j - i;
}
}
else
{
flag[i][j] = false;
}
}
}
return s.substring(index, index + maxLength + 1);
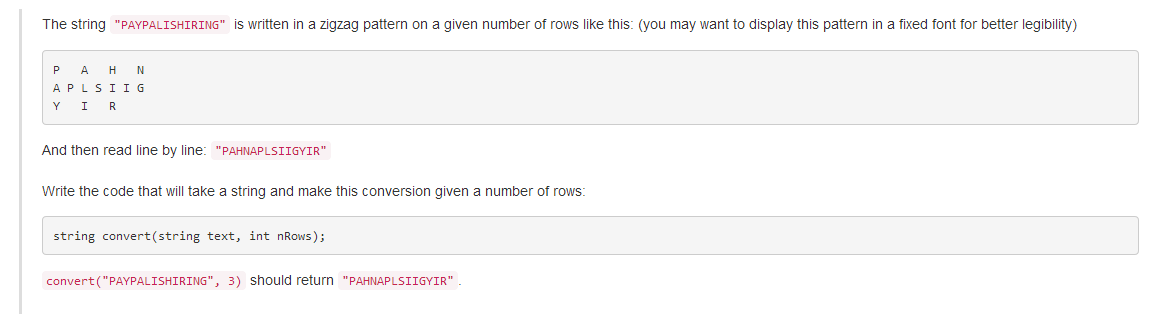
}6.ZigZag Conversion
这道题的目的是要你将字符串的每个字符排列成锯齿形状再按每一行依次输出。先考虑如何弄成锯齿形状。
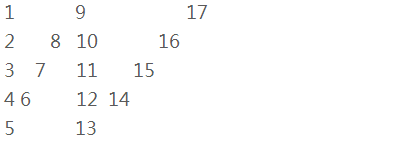
如果要弄成锯齿状输出,那么控制下Console.WriteLine()和Console.Write()的时机就可以完成,但这里是要求打印锯齿状后的每一行。
以行数为5为例,观察上面锯齿的产生过程,对于斜行,其都是夹在相邻两行起点和终点之间的,那么斜行的元素个数必然会少2。即斜行的元素个数都是行数rows-2。这个因素定下来了,后面的就不会顺序就不会有改变了。
跑分90%。
public string Convert(string s, int numRows) {
if (numRows == 1)
{
return s;
}
char[] arr = s.ToCharArray();
StringBuilder result = new StringBuilder();
StringBuilder[] str = new StringBuilder[numRows];
for (int i = 0; i < str.Length; i++)
{
str[i] = new StringBuilder();
}
int index = 0;
int j = 0;
while (index < arr.Length)
{
for (j = 0; index < arr.Length && j < numRows; index++)
{
str[j++].Append(arr[index]);
}
for (j = numRows - 2; index < arr.Length && j > 0; )
{
str[j--].Append(arr[index++]);
}
}
for(int i = 0; i < str.Length; i++)
{
result.Append(str[i].ToString());
}
return result.ToString();
}7.Reverse Integer
能用%,/运算符分割出每一位就别用转换成字符串来描述。能用每次取个位后乘10升位来反转就别用字符串来对字符做交换。
做超限处理。
注意int的表示范围。
跑分30%。低。。
public int Reverse(int x) {
Int64 result = 0;
while (x != 0)
{
int i = x % 10;
result = result * 10 + i;
if (result > Int32.MaxValue || result < Int32.MinValue)
{
result = 0;
break;
}
x /= 10;
}
return (int)result;
}8.String to Integer (atoi)
这道题提交了很多次,题没审清,英文描述没去细细读。
int超界是个头疼的事情,用Int64来装都被一个测试用例超界反转了。
最后跑分已惨不忍睹。还得改。
public int MyAtoi(string str) {
str = str.Trim();
if (string.IsNullOrEmpty(str))
{
return 0;
}
char[] arr = str.ToCharArray();
Int64 result = 0;
int bit = 0;
bool negative = false;
if (!(arr[0] == 43 || arr[0] == 45 || arr[0] > 47 && arr[0] < 58))
{
return 0;
}
if (arr[0] == 43 || arr[0] == 45)
{
if (arr.Length == 1 || !(arr[1] > 47 && arr[1] < 58))
{
return 0;
}
}
if (arr[0] == 45)
{
negative = true;
}
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] > 47 && arr[i] < 58)
{
bit++;
result = result * 10 + int.Parse(arr[i].ToString());
if (i < arr.Length - 1)
{
if (arr[i + 1] <= 47 || arr[i + 1] >= 58)
{
break;
}
}
}
}
if (negative)
{
result *= -1;
}
if (bit > 10 || result > Int32.MaxValue || result < Int32.MinValue)
{
result = negative ? Int32.MinValue : Int32.MaxValue;
}
return (int)result;
}9.Palindrome Number
相对于第5题求最长回文子串,这道题就简单很多了,因为开始结束位置都是确定了的。
跑分60%。
public bool IsPalindrome(int x) {
//// -109 和 901-才是回文
if (x < 0)
{
return false;
}
int ori = x;
int res = 0;
while (ori > 0)
{
res = res * 10 + ori % 10;
ori /= 10;
}
return res == x;
}1-9道算法题的记录到这里就完成了。后面再继续了。


























 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








