TensorFlow神经网络优化：复杂学习率、激活函数、损失函数、过拟合、梯度爆炸、优化器

1. 神经网络的复杂度

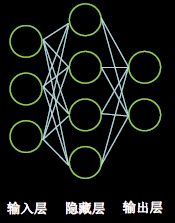
1.1时间复杂度

  时间复杂度即模型的运算次数，可用浮点运算次数（FPLOPs, FLoating-point OPerations）或者乘加运算次数衡量。上图中神经网络乘加运算次数：
$$3\times 4+4\times 2=20$$

1.2空间复杂度

  空间复杂度（访存量），严格来讲包括两部分：总参数量 + 各层输出特征图。

• 参数量：模型所有带参数的层的权重参数总量；
• 特征图：模型在实时运行过程中每层所计算出的输出特征图大小。

  上图中，层数=隐藏层层数+1个输出层=2层NN；总参数=总w+总b=$(3\times 4+4)+(4\times 2+2)=26$。

2. 复杂学习率

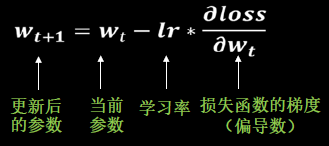
2.1指数衰减学习率

  指数衰减学习率在训练初期赋予网络较大学习率，快速得到一个较优的解，然后逐步减小学习率，使模型在训练后期稳定。指数型学习率衰减法是最常用的衰减方法，在大量模型中都广泛使用。
$$指数衰减学习率=初始学习率\ast 学习率衰减{率}^{当前轮数/多少轮衰减一次}$$

实验对比

$$loss=(w+1{)}^2$$

• 固定学习率：

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  # 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环40次迭代。
    with tf.GradientTape() as tape:  # with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  # .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

• 指数衰减学习率：

w = tf.Variable(tf.constant(5, dtype=tf.float32))

epoch = 40
LR_BASE = 0.2  # 最初学习率
LR_DECAY = 0.99  # 学习率衰减率
LR_STEP = 1  # 喂入多少轮BATCH_SIZE后，更新一次学习率

for epoch in range(epoch):  # 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环100次迭代。
    lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
    with tf.GradientTape() as tape:  # with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  # .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f,lr is %f" % (epoch, w.numpy(), loss, lr))

TensorFlow API

第一种：
tf.compat.v1.train.exponential_decay(learning_rate_base,global_step,decay_step,decay_rate,staircase =True(False),name)
当staircase为True时，学习率呈现阶梯状递减。

第二种：
声明tf.keras.optimizers.schedules.ExponentialDecay(initial_learning_rate, decay_steps, decay_rate, staircase=False, name=None)

• initial_learning_rate: 初始学习率.
• decay_steps: 衰减步数, staircase为True时有效.
• decay_rate: 衰减率.
• staircase: Bool型变量.如果为True, 学习率呈现阶梯型下降趋势.

调用tf.keras.optimizers.schedules.ExponentialDecay(step)返回计算得到的学习率。

N = 400
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(
0.5,
decay_steps=10,
decay_rate=0.9,
staircase=False)
y = []
for global_step in range(N):
lr = lr_schedule(global_step)
y.append(lr)
x = range(N)
plt.figure(figsize=(8,6))
plt.plot(x, y, 'r-')
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Step')
plt.ylabel('Learning Rate')
plt.title('ExponentialDecay')
plt.show()

2.2 分段常数衰减学习率

  分段常数衰减可以让调试人员针对不同任务设置不同的学习率，进行精细调参，在任意步长后下降任意数值的learning rate，要求调试人员对模型和数据集有深刻认识。

TensorFlow API

声明tf.keras.optimizers.schedules.PiecewiseConstantDecay(boundaries, values, name=None)

• boundaries: [step_1, step_2, …, step_n]定义了在第几步进行学习率衰减.
• values: [val_0, val_1, val_2, …, val_n]定义了学习率的初始值和后续衰减时的具体取值.

调用tf.keras.optimizers.schedules.PiecewiseConstantDecay(step)返回计算得到的学习率.

N = 400
lr_schedule = tf.keras.optimizers.schedules.PiecewiseConstantDecay(
boundaries=[100, 200, 300],
values=[0.1, 0.05, 0.025, 0.001])
y = []
for global_step in range(N):
lr = lr_schedule(global_step)
y.append(lr)
x = range(N)
plt.figure(figsize=(8,6))
plt.plot(x, y, 'r-')
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Step')
plt.ylabel('Learning Rate')
plt.title('PiecewiseConstantDecay')
plt.show()

3. 激活函数

  激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。引入非线性激活函数，可使深层神经网络的表达能力更加强大。

  优秀的激活函数应满足：

• 非线性： 激活函数非线性时，多层神经网络可逼近所有函数；
• 可微性： 优化器大多用梯度下降更新参数；
• 单调性： 当激活函数是单调的，能保证单层网络的损失函数是凸函数；
• 近似恒等性：$f(x)\approx x$，当参数初始化为随机小值时，神经网络更稳定。

  激活函数输出值的范围：

• 激活函数输出为有限值时，基于梯度的优化方法更稳定；
• 激活函数输出为无限值时，建议调小学习率。

  关于激活函数选择的建议：

• 首选ReLU激活函数；
• 学习率设置较小值；
• 输入特征标准化，即让输入特征满足以0为均值，1为标准差的正态分布；
• 初始参数中心化，即让随机生成的参数满足以0为均值，$\sqrt{\frac{2}{当前层输入特征个数}}$为标准差的正态分布。

3.1Sigmoid函数

$$f(x)=\frac{1}{1+e^{-x}}$$

特点：

• 相当于进行了归一化；
• 易造成梯度消失：深层神经网络需要从输出层到输入层逐层链式求导，链式求导需要多层导数连续相乘，0~0.25之间的数相乘，会产生梯度消失问题，无法进行参数更新；
• 输出非0均值，收敛慢：期望输入每层神经网络的特征是以0为均值的小数值，但是sigmoid函数的输出均是正数，会使收敛变慢；
• 幂运算复杂，训练时间长。

  sigmoid函数可应用在训练过程中。然而，当处理分类问题作出输出时，sigmoid却无能为力。简
单地说，sigmoid函数只能处理两个类，不适用于多分类问题。而softmax可以有效解决这个问题，并
且softmax函数大都运用在神经网路中的最后一层网络中，使得值得区间在（0,1）之间，而不是二分类
的。

神经网络图像输入零均值化的作用：
零均值化可以避免“Z型更新”的情况，这样可以加快神经网络的收敛速度。

TensorFlow API

tf.math.sigmoid(x, name=None)：计算x每一个元素的sigmoid值，返回与x shape相同的张量。

x = tf.constant([1., 2., 3.], )
print(tf.math.sigmoid(x))

运行结果：

tf.Tensor([0.7310586 0.880797 0.95257413], shape=(3,), dtype=float32)

等价实现：

print(1/(1+tf.math.exp(-x)))

运行结果：

tf.Tensor([0.7310586 0.880797 0.95257413], shape=(3,), dtype=float32)

3.2Tanh函数

$$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

特点：

• 输出是0均值
• 易造成梯度消失
• 幂运算复杂，训练时间长

TensorFlow API

tf.math.tanh(x, name=None)：计算x每一个元素的双曲正切值。

x = tf.constant([-float("inf"), -5, -0.5, 1, 1.2, 2, 3, float("inf")])
print(tf.math.tanh(x))

运行结果：

tf.Tensor([-1. -0.99990916 -0.46211717 0.7615942 0.8336547 0.9640276
0.9950547 1.], shape=(8,), dtype=float32)

等价实现：

print((tf.math.exp(x)-tf.math.exp(-x))/(tf.math.exp(x)+tf.math.exp(-x)))

运行结果：

tf.Tensor([nan -0.9999091 -0.46211714 0.7615942 0.83365464 0.9640275
0.9950547 nan], shape=(8,), dtype=float32)

3.3ReLU函数

$$f(x)=max(x,0)=\{\begin{array}{l}0,x<0\\ x,x\ge 0\end{array}$$

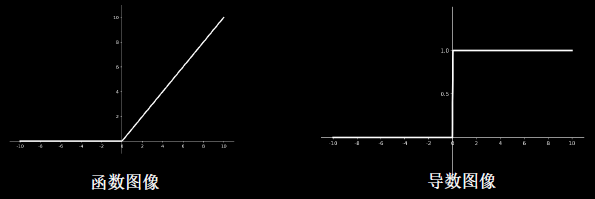
优点：

• 解决了梯度消失问题(在正区间)
• 只需判断输入是否大于0，计算速度快
• 收敛速度远快于sigmoid和tanh

缺点：

• 输出非0均值，收敛慢
• Dead RelU问题：某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。
  • 送入激活函数的特征是负数时，激活函数输出是0，反向传播得到的梯度是0，导致参数无法继续更新，造成神经元死亡。所以神经元死亡的根本原因是，经过ReLU函数的负数特征过多。
  • 改进：1.改进随机初始化：避免过多的负数特征送入ReLU函数；2.设置更小的学习率：减小参数分布的巨大变化，避免训练中产生过多负数特征进入ReLU函数。

TensorFlow API

tf.nn.relu(features, name=None)：计算修正线性值(rectified linear)：max(features, 0)，返回与features shape相同的张量。

print(tf.nn.relu([-2., 0., -0., 3.]))

运行结果：

tf.Tensor([0. 0. -0. 3.], shape=(4,), dtype=float32)

3.5Leaky ReLU函数

$$f(x)=max(\alpha x,x)$$

理论上来讲，Leaky Relu有Relu的所有优点，外加不会有Dead Relu问题，但是在实际操作当中，并没有完全证明Leaky Relu总是好于Relu。

TensorFlow API

tf.nn.leaky_relu(features, alpha=0.2, name=None)：计算Leaky ReLU值，返回与features shape相同的张量。

print(tf.nn.leaky_relu([-2., 0., -0., 3.]))

运行结果：

tf.Tensor([-0.4 0. -0. 3.], shape=(4,), dtype=float32)

3.6softmax

$$\sigma (z{)}_j=\frac{e^{z_j}}{{\sum }_{k=1}^K{e}_{z_k}}forj=1,...,K$$

对神经网络全连接层输出进行变换，使其服从概率分布，即每个值都位于[0,1]区间且和为1。

TensorFlow API

tf.nn.softmax(logits, axis=None, name=None)：计算softmax激活值，返回与logits shape相同的张量。

• logits: 张量.
• axis: 计算softmax所在的维度. 默认为-1，即最后一个维度.

logits = tf.constant([4., 5., 1.])
print(tf.nn.softmax(logits))

运行结果：

tf.Tensor([0.26538792 0.7213992 0.01321289], shape=(3,), dtype=float32)

等价实现：

print(tf.exp(logits) / tf.reduce_sum(tf.exp(logits)))

运行结果：

tf.Tensor([0.26538792 0.72139925 0.01321289], shape=(3,), dtype=float32)

4. 损失函数

  损失函数衡量了预测值与真实值的差距。

4.1均方误差损失函数

  均方误差（Mean Square Error）是回归问题最常用的损失函数。回归问题需要预测的不是一个事先定义好的类别，而是一个任意实数。均方误差定义如下：
$$MSE(y,\hat{y})=\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{n}$$

其中$y_i$为一个batch中第 $i$ 个数据的真实值，而${\hat{y}}_i$为神经网络的预测值。

TensorFlow API

tf.keras.losses.MSE(y_true, y_pred)：计算y_true和y_pred的均方误差。

y_true = tf.constant([0.5, 0.8])
y_pred = tf.constant([1.0, 1.0])
print(tf.keras.losses.MSE(y_true, y_pred))

运行结果：

tf.Tensor(0.145, shape=(), dtype=float32)

等价实现：

print(tf.reduce_mean(tf.square(y_true - y_pred)))

运行结果：

tf.Tensor(0.145, shape=(), dtype=float32)

4.2交叉熵损失函数

  交叉熵（Cross Entropy）表征两个概率分布之间的距离，交叉熵越小说明二者分布越接近，是分类问题中使用较广泛的损失函数。

$$H(y,\hat{y})=-\sum y\ln \hat{y}$$

其中$y$代表数据的真实值，而$\hat{y}$为神经网络的预测值。

  对于多分类问题，神经网络的输出一般不是概率分布，因此需要引入softmax层，使得输出服从概
率分布。

TensorFlow API

tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)：计算交叉熵。

• y_true: 真实值
• y_pred: 预测值
• from_logits: y_pred是否为logits张量
• label_smoothing: [0,1]之间的小数

y_true = [1, 0, 0]
y_pred1 = [0.5, 0.4, 0.1]
y_pred2 = [0.8, 0.1, 0.1]
print(tf.keras.losses.categorical_crossentropy(y_true, y_pred1))
print(tf.keras.losses.categorical_crossentropy(y_true, y_pred2))

运行结果：

tf.Tensor(0.6931472, shape=(), dtype=float32)
tf.Tensor(0.22314353, shape=(), dtype=float32)

等价实现：

print(-tf.reduce_sum(y_true * tf.math.log(y_pred1)))
print(-tf.reduce_sum(y_true * tf.math.log(y_pred2)))

运行结果：

tf.Tensor(0.6931472, shape=(), dtype=float32)
tf.Tensor(0.22314353, shape=(), dtype=float32)

tf.nn.softmax_cross_entropy_with_logits(labels, logits, axis=-1, name=None)：logits经过softmax后，与labels进行交叉熵计算。在机器学习中，对于多分类问题，把未经softmax归一化的向量值称为logits。

• labels: 在类别这一维度上，每个向量应服从有效的概率分布. 例如，在labels的shape为[batch_size, num_classes]的情况下，labels[i]应服从概率分布
• logits: 每个类别的激活值，通常是线性层的输出. 激活值需要经过softmax归一化
• axis: 类别所在维度，默认是-1，即最后一个维度

labels = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0]]
logits = [[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]]
print(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))

运行结果：

tf.Tensor([0.16984604 0.02474492], shape=(2,), dtype=float32)

等价实现：

print(-tf.reduce_sum(labels * tf.math.log(tf.nn.softmax(logits)), axis=1))

运行结果：

tf.Tensor([0.16984606 0.02474495], shape=(2,), dtype=float32)

tf.nn.sparse_softmax_cross_entropy_with_logits(labels, logits, name=None)：labels经过one-hot编码，logits经过softmax，两者进行交叉熵计算. 通常labels的shape为[batch_size]，logits的shape为[batch_size, um_classes]. sparse可理解为对labels进行稀疏化处理(即进行one-hot编码).

• labels: 标签的索引值.
• logits: 每个类别的激活值，通常是线性层的输出. 激活值需要经过softmax归一化.

labels = [0, 1]
logits = [[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]]
print(tf.nn.sparse_softmax_cross_entropy_with_logits(labels1, logits))

运行结果：

tf.Tensor([0.16984604 0.02474492], shape=(2,), dtype=float32)

等价实现：

print(-tf.reduce_sum(tf.one_hot(labels, tf.shape(logits)[1]) * tf.math.log(tf.nn.softmax(logits)), axis=1))

运行结果：

tf.Tensor([0.16984606 0.02474495], shape=(2,), dtype=float32)

4.3自定义损失函数

  根据具体任务和目的，可设计不同的损失函数。好的损失函数设计对于模型训练能够起到良好的引导作用。

5. 缓解过拟合

欠拟合的解决方法：

• 增加输入特征项
• 增加网络参数
• 减少正则化参数

过拟合的解决方法：

• 数据清洗
• 增大训练集
• 采用正则化
• 增大正则化参数

5.1正则化缓解过拟合

  正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声（一般不正则化b）。正则化的选择：

• L1正则化大概率会使很多参数变为零，因此该方法可通过稀疏参数，即减少参数的数量，降低复杂度。
• L2正则化会使参数很接近零但不为零，因此该方法可通过减小参数值的大小降低复杂度。

with tf.GradientTape() as tape:  # 记录梯度信息

	h1 = tf.matmul(x_train, w1) + b1  # 记录神经网络乘加运算
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2

    # 采用均方误差损失函数mse = mean(sum(y-out)^2)
    loss_mse = tf.reduce_mean(tf.square(y_train - y))
    # 添加l2正则化
    loss_regularization = []
    loss_regularization.append(tf.nn.l2_loss(w1))
    loss_regularization.append(tf.nn.l2_loss(w2))
    loss_regularization = tf.reduce_sum(loss_regularization)
    loss = loss_mse + 0.03 * loss_regularization #REGULARIZER = 0.03

# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)

6. 处理梯度爆炸

  分析差生梯度爆炸的原因，考虑到梯度下降计算公式：
$$w_{new}=w_{old}-lr\cdot \frac{\partial L}{\partial w}$$

参数更新量为学习率与损失函数偏导数相乘，二者乘积过大，则会导致梯度爆炸。因此，解决梯度爆炸问题可针对学习率进行调整，也可对数据进行调整。故解决方法可为：

(1)逐步减小学习率，0.1、0.01等；

(2)对数据进行预处理后再输入神经网络，减小偏差值的大小，抑制梯度爆炸，即数据归一化与标准化，其主要方法有:

• 线性归一化：将数据映射到[0,1]区间中，
  $$x^{\ast }=\frac{x-min(x)}{max(x)-min(x)}$$
• 非线性归一化(log函数转换)：使数据映射到[0,1]区间上，
  $$x^{\ast }=\frac{lo{g}_{10}x}{lo{g}_{10}max(x)}$$
• Z-Score标准化：使每个特征中的数值平均值变为0，标准差变为1，
  $$x^{\ast }=\frac{x-mean(x)}{std(x)}$$

#线性归一化
def normalize(data):
	x_data = data.T # 每一列为同一属性，转置到每一行
	for i in range(4):
		x_data[i] = (x_data[i] - tf.reduce_min(x_data[i])) / (tf.reduce_max(x_data[i]) - 		tf.reduce_min(x_data[i]))
	return x_data.T # 转置回原格式

7. 优化器

  优化算法可以分成一阶优化和二阶优化算法，其中一阶优化就是指的梯度算法及其变种，而二阶优化一般是用二阶导数（Hessian 矩阵）来计算，如牛顿法，由于需要计算Hessian阵和其逆矩阵，计算量较大，因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。
  深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam
这样的发展历程。

待优化参数 $w$，损失函数$loss$ ，初始学习率$lr$ ，每次迭代一个batch，$t$ 表示当前batch迭代的总次数：

1. 计算损失函数关于当前参数的梯度：$g_t=\nabla loss(w_t)=\frac{\partial loss}{\partial w_t}$
2. 根据历史梯度计算一阶动量$m_t=\varphi (g_1,g_2,...,g_t)$和二阶动量$V_t=\psi (g_1,g_2,...,g_t)$：一阶动量是与梯度相关的函数，二阶动量是与梯度平方相关的函数
3. 计算当前时刻的下降梯度：${\eta }_t=lr\cdot m_t/\sqrt{V_t}$
4. 根据下降梯度进行更新：$w_{t+1}=w_t-{\eta }_t$

步骤3，4对于各算法都是一致的，主要差别体现在步骤1和2上。

7.1SGD（无momentum）

• 常用的梯度下降法

$$\{\begin{array}{l}{m}_t=g_t\\ V_t=1\\ {\eta }_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t\\ w_{t+1}=w_t-{\eta }_t=w_t-lr\cdot g_t\end{array}$$

# 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
w1.assign_sub(lr * grads[0])  # 参数w1自更新
b1.assign_sub(lr * grads[1])  # 参数b自更新

7.2SGDM（含momentum的SGD）

• 在SGD基础上增加一阶动量

$$\{\begin{array}{l}{m}_t=\beta \cdot m_{t-1}+(1-\beta )\cdot g_t\\ V_t=1\\ {\eta }_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot m_t=lr\cdot (\beta \cdot m_{t-1}+(1-\beta )\cdot g_t)\\ w_{t+1}=w_t-{\eta }_t=w_t-lr\cdot (\beta \cdot m_{t-1}+(1-\beta )\cdot g_t)\end{array}$$

m_w, m_b = 0, 0
beta = 0.9

# sgd-momentun  
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)

7.3Adagrad

• 在SGD基础上增加二阶动量

$$\{\begin{array}{l}{m}_t=g_t\\ V_t={\sum }_{\tau =1}^t{g}_{\tau }^2\\ {\eta }_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t/(\sqrt{{\sum }_{\tau =1}^t{g}_{\tau }^2})\\ w_{t+1}=w_t-{\eta }_t=w_t-lr\cdot g_t/(\sqrt{{\sum }_{\tau =1}^t{g}_{\tau }^2})\end{array}$$

v_w, v_b = 0, 0

# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

7.4RMSProp

• 在SGD基础上增加二阶动量

$$\{\begin{array}{l}{m}_t=g_t\\ V_t=\beta \cdot V_{t-1}+(1-\beta )\cdot g_t^2\\ {\eta }_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t/\sqrt{\beta \cdot V_{t-1}+(1-\beta )\cdot g_t^2}\\ w_{t+1}=w_t-{\eta }_t=w_t-lr\cdot g_t/\sqrt{\beta \cdot V_{t-1}+(1-\beta )\cdot g_t^2}\end{array}$$

v_w, v_b = 0, 0
beta = 0.9

# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

7.5Adam

• 同时结合SGDM一阶动量和RMSProp二阶动量

$$\{\begin{array}{l}{m}_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t\\ {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}\\ V_t={\beta }_2\cdot V_{t-1}+(1-{\beta }_2)\cdot g_t^2\\ {\hat{V}}_t=\frac{V_t}{1-{\beta }_2^t}\\ {\eta }_t=lr\cdot {\hat{m}}_t/\sqrt{{\hat{V}}_t}=lr\cdot \frac{m_t}{1-{\beta }_1^t}/\sqrt{\frac{V_t}{1-{\beta }_2^t}}\\ w_{t+1}=w_t-{\eta }_t=w_t-lr\cdot \frac{m_t}{1-{\beta }_1^t}/\sqrt{\frac{V_t}{1-{\beta }_2^t}}\end{array}$$

m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0

# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])

m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))

w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))

---

北大人工智能实践：Tensorflow笔记