查询子字符串：一篇文章读懂KMP算法

KMP算法可以用于在一个字符串中是否包含某个子字符串，比常规双重循环算法的效率高，但是此算法初次接触可能不太容易理解，等到理解之后会感觉很简单。为了方便大家快速理解KMP算法的过程，我制作了两个动态图，一个是常规算法，一个是KMP算法，清晰易懂。

有两个字符串：

source：bababaabd

target：abaabd

要求在source中查询target字符串第一次出现的位置。

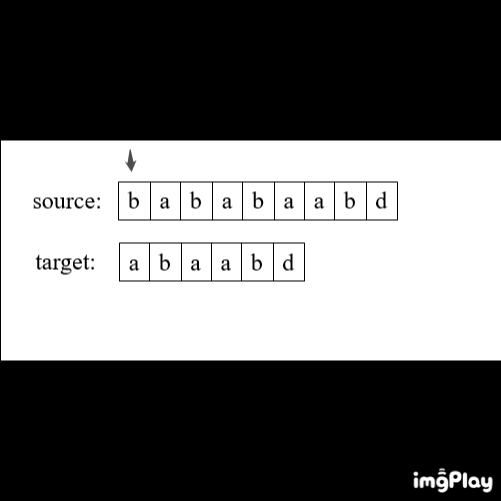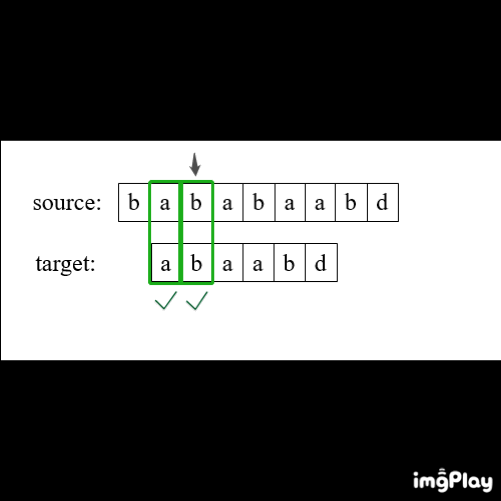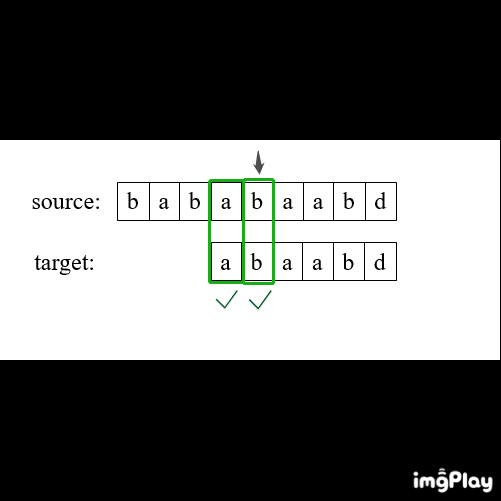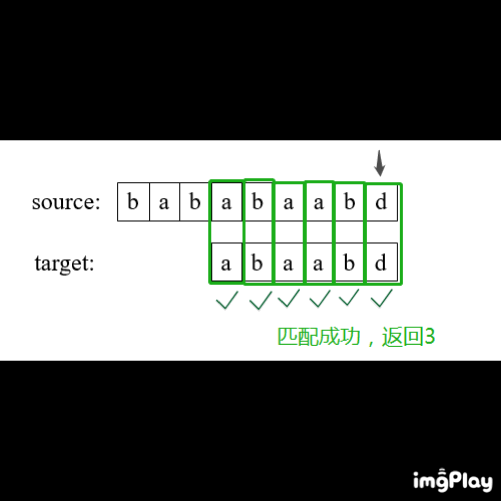
常规算法的动态图：

KMP算法的动态图：

常规方法：双重循环

1、初始化i=0,j=0

2、开始循环：

     如果source[i] == target[j]，则 i++,j++；

            如果 j == len(target)，返回 i - j

     否则 i = i - j + 1,j=0

     直至 i == len(source)

时间复杂度为 O(m*n)。m = len(source),n = len(target)

KMP算法：一重循环

1、初始化 i = 0, j = 0

2、开始循环：

     如果source[i] == target[j]，则 i++,j++；

            如果 j == len(target)，返回 i - j

     否则 j = next[j]，如果此时 j == -1，则 j = 0, i++。

     直至 i == len(source)

时间复杂度为 O(m)。

 两个算法只有标黄部分有区别。其中KMP算法中涉及到了 next 数组，这个数组表示target字符串的每个截断字符串的前后缀最长相同字符串的长度。

比如字符串  abab，它的前缀包括 a，ab，aba，后缀包括 b，ab，bab（前缀不能包括最后一个字符，后缀不能包括第一个字符）。所以前后缀相同的最长长度为2，即前缀=后缀=ab。

同理分析target字符串的每个截断字符串：

索引	截断字符串	最长前后缀	长度
0	a	无	0
1	ab	无	0
2	aba	a	1
3	abaa	a	1
4	abaab	ab	2
5	abaabd	无	0

所以最长匹配前后缀的长度数组为 [0,0,1,1,2,0]

注意next数组的定义是， next[j] 存放的是长度为 j-1 的截断字符串（而不是长度为j）的最长前后缀长度。因此 next = [-1, 0, 0, 1, 1, 2]。这个是因为，如果匹配到 target[j] 时变成红叉，则我们下一步移动的 target 的位置与当前的 target[j] 值无关，只与前 j-1 个字符有关。我们定义 next[0] = -1。

有了 next 数组的意义，就知道为什么当出现红叉时，只要 j = next[j] 就可以了。比如动态图中的：

走到 target[3] 时字符不再相等，出现了红叉，那么如果按照常规双重循环的算法，下一步应该是箭头回溯到 target 起点的下一个：

但是 KMP 算法不用回溯，箭头仍然停留在 source[4] 上，只需要让 target[next[3]] 即 target[1] 对准箭头即可，如图：

此时 target[1] 之前的所有字符（这里只有一个“a”）肯定与 source 的字符是匹配上的，不用检验，原因是：target 的 aba 已经匹配到了 source 的 aba ，而 a 是字符串 aba 的前后缀匹配字符串之一（确切说是最长的），所以，如果 target 的第一个字符 a 可以匹配 source 的第一个字符，那么肯定可以匹配 source 的最后字符。所以箭头之前的所有字符都肯定是一一匹配的，不必检验。只需要继续比对当前箭头位置的字符是否匹配即可，即比较 target[1] 与 source[4] 是否相等。这里是相等的，都是 b，假如不相等，那么继续让 target 的下标经过 next 映射即可，即让 target[next[next[3]]] = target[next[1]] = target[0] 对齐箭头即可。如果 target[0] 仍然不匹配，继续进行 next 映射，next[0] = -1，说明这个箭头所在位置肯定不能使得 target 字符串匹配成功了，只能让箭头向右移动一格，且重置 target 下标使得 target的第一个字符对准箭头，用相同的方法进行搜索。

用这种思想，就实现了箭头不回退就可以搜索到子字符串的功能。

        剩下的唯一问题就是，如何计算 next 数组。

有两种方法，第一种是按照 next 定义，对每一个截断字符串，都从长度1开始慢慢增加，判断前后缀是否相同，直至出现不同前后缀停止，就找到了最长前后缀字符串了。但是这种方法的缺点在于，每一个截断字符串都要重新计算，没有利用好之前计算出的结果。

所以我们采用第二种方法：根据已经计算出的 next[0:j]，推导出 next[j+1]的值。

拿一个更有代表性的例子，比如我们已经计算出了 abadaba 的最长匹配前后缀为 aba，那么后面新来一个字符 b 之后，新的字符串 abadabab 的最长匹配前后缀是什么？

1、首先我们拿出原字符串的最长匹配前后缀 aba，然后加上 b，变为 abab，这是后缀，然后看前缀是否也等于 abab。如果是的话，abab 就是新字符串的最长匹配前后缀（用反证法可以证明是最长的：假如还有更长的前后缀，如 xabab，那么 xaba 肯定是原字符串的匹配前后缀，那么 aba 就不是最长的了，与已知矛盾）。

2、但是我们这个例子，前缀是 abad，不等于 abab。所以要缩短后缀的长度，然后继续比较。缩短后缀的方法有两种：

（1）可以一个字符一个字符的缩短，即依次校验 abab、bab、ab、b，直到匹配上前缀，如果都匹配不上，那就是0；

（2）也可以用更快的方法，那就是将后缀直接定为 aba 的最长前后缀（即 a）加上新字符 b，即 ab，然后判断前缀是否是 ab，如果是，那么新字符串的最长匹配前后缀就是 ab 了。如果不是，那再将后缀直接定为 a 的最长前后缀（为空）加上新字符 b，即 b，然后判断前缀是否是 b，以此类推。

       第二种缩短后缀的方法与第一种相比，略去了 bab 这个后缀，因为这个后缀肯定是不等于前缀的（证明：假如前缀等于后缀，也是 bab，那么 ba 肯定也是 aba 的匹配前后缀之一了，这与 a 是 aba 的最长前后缀矛盾）。

总结根据已经计算出的 next[0:j]，推导出 next[j+1]的值的算法：

1、k = next[j]

2、开始循环：

          如果 k = -1，则 next[j+1] = 0，算法结束

          target[j] 是否等于 target[k]，如果等于，则 next[j+1] = k + 1，算法结束

          否则令 k = next[k]，继续循环。

KMP代码：

 1# 问题：给定两个字符串A和B，要求判断A是否包含B，如果包含返回第一次出现B的index
 2class FindSubStr:
 3    def __init__(self, source, target):
 4        self.source = source
 5        self.target = target
 6    # 最传统的方法，双重循环，O(m*n)
 7    def findByCommon(self):
 8        if self.source is None or self.target is None:
 9            return -1
10        for i in range(len(self.source) - len(self.target) + 1):
11            for j in range(len(self.target)):
12                if self.source[i + j] != self.target[j]:
13                    break
14            else: # 此else对应的是for，表示for循环没有被break过
15                return i
16        return -1
17    # 新的方法，O(m) + O(n)
18    def findByKMP(self):
19        if self.source is None or self.target is None:
20            return -1
21        '''
22        根据已有的next_list，求下一个next的值
23        '''
24        def getNext(self, next_list):
25            idx = len(next_list) - 1 # 当前next_list的最大索引
26            if idx == -1: # next为空，所求为第一个字符的next值，固定为-1
27                return -1
28            k = next_list[idx] # next_list最后一位的值
29            while k != -1:
30                if self.target[idx] == self.target[k]: # 新来的值是否等于最长匹配前后缀后面的那个字符
31                    return k+1
32                k = next_list[k] # 更新最长匹配前后缀的长度
33            return 0
34        # 构造next数组
35        next_list = list()
36        while len(next_list) < len(self.target):
37            next_list.append(getNext(self, next_list))
38        print('next_list:',next_list)
39        # 开始检索
40        i = 0 # source字符串的索引
41        j = 0 # target字符串的索引
42        while i < len(self.source):
43            if self.source[i] == self.target[j]: # 字符相同，则都往右移一位继续比较
44                i += 1
45                j += 1
46                if j == len(self.target): # target的最后一个字符都匹配到了，则匹配成功
47                    return i - j # 返回匹配字符串的第一个字符的索引，所以需要减去子字符串长度
48            else:
49                j = next_list[j] # 字符不同，按照next_list更新target的索引
50                if j == -1: # 因为next_list[0]=-1，所以说明当前的source字符连target的第一个字符都不匹配，则从source的下一个字符开始检索
51                    j = 0
52                    i += 1
53        return -1
54if __name__ == '__main__':
55    S = FindSubStr('bababaabd','abaabd')
56    print('source:',S.source) 
57    print('target:',S.target)
58    print(S.findByCommon())
59    print(S.findByKMP())  

KMP代码地址：https://github.com/HappyRocky/pythonAI/blob/master/algorithm-exercise/FindSubStr.py

欢迎关注我的公众号：