Submodularity beyond submodular energies: Coupling edges in graph cuts
Conference: Conference: The 24th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2011, Colorado Springs, CO, USA, 20-25 June 2011
子模块性的超越子模块能量:
图切割中的耦合边缘
我们提出了一个新的非子模块全局能量函数族,它仍然在内部使用子模块来耦合边缘在graph cut中。我们表明有可能开发一个高效的近似算法,由于内部子模块,可以使用标准graph cut作为子程序。我们证明了在自然情境中边缘耦合的优势,即 image segmentation。特别是,对于具有精细结构的对象和具有阴影变化的对象,我们的结构化边缘耦合得到的效果比标准方法有着显著的提高。
第一节导论
多年来,马尔可夫随机场(MRF)被认为是解决计算机视觉中的各种问题的天作之合[ 12 ]。在这样的模型中,寻找随机变量值的最大分配符合Gibbs能量最小化。这种最小化一般不仅是NP难,而且有些模型甚至不承认任何非平凡的近似保证[ 5 ]。因此,对于图像处理,一些早期的研究人员认为MRF仅仅是一种理论上的好奇。
最近,MRF的子类被证明不仅容易精确优化(没有树宽度限制),而且很自然地适用于许多计算机视觉问题[ 4 ],[ 12 ],[ 23 ]。 具体而言,寻找最小能量配置对于那些可变分配成本完全对应于合适的图中的降低成本的Gibbs能量函数[ 8 ],[ 23 ]是非常有效的。Graph cut现在已成功用于分割,立体匹配和纹理合成等等。
受这些结果的启发,一个主要目标已经变成识别可以通过Graph cut直接的或者间接的精确优化的最一般能量类别。例如,一些二元成对势函数可以使用Graph cut来精确求解,很多情况是更高阶(例如, ,k-ary)势函数[ 8 ],[ 23 ],[ 33 ]和非二元变量[ 4 ]的势函数也可以有效解决。 在所有情况下,一个被称为“regularity”[ 23 ](更一般地说,子模块性[ 9 ])的关键属性在被使用。
不幸的是,在实践中使用Graph cut时存在严重的缺陷,部分原因是它们仅仅只是有限的能量类别[ 8 ],[ 10 ],[ 23 ],[ 33 ]上有用。核心问题在于,Graph cut模型是一种能将非负权值分解成成对的项的能量。这种能量的直接使用会导致图像分割中不可克服的过度平滑。虽然一些更高阶的能量是图表可表示的,但是这种表示可能会遗憾地需要额外的变量,这些变量在计算上也不可行[ 33 ]。 因此,最近的研究旨在确定实际上可管理的高阶能量[ 15],[ 18 ],[ 19 ],[ 24 ],并对非子模块电势开发有效的优化方法[ 22 ]。
在这项工作中,我们定义了一个新的强大的任意高阶非子模块能量函数类,它既不放弃一个底层图的存在,也不使用子模块性,也不具有实用效率。 这个类在结构上和概念上与最近在[ 15 ],[ 18 ],[ 24 ]中所考虑的电势大不相同。因此,我们提出如下关键的观察:如果构成一切割边缘的成本不仅仅是根据边权重的总和来衡量,那么Graph cut的能量函数可以得到极大的提高。相反,在我们的工作中,图中的任何或所有边可能以复杂的方式相互作用。形式上就是,让 成为一个每个 -cut都能引起像素标签的分配的图像。我们用子模块削减成本替换通常的削减成本(边权重的总和),因此我们说边界本身可以合作 [ 30 ]。这样做会引起以下问题:
定义1
(最小Cooperative Cut)。给定一个图 和一个不降低的子模块功能 定义在边的子集上 ,找到一个 -cut 使到成本最低 。
如下所示,等效能量函数通常不是一般的子模块,合作切割是NP难的,即使在某种意义上子模块是我们的问题的“内在”,正如将要看到的那样。图结构是获得高效逼近算法的关键。
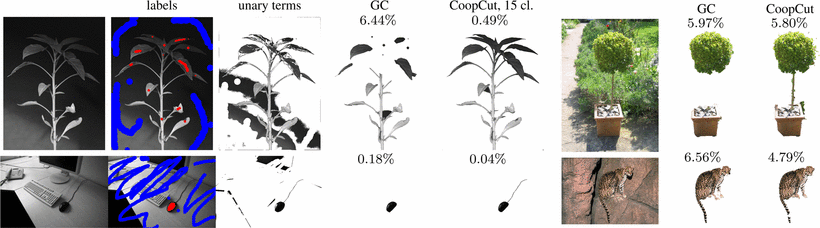
图1.分割结果为带阴影的图像。尽管有许多标签,任务仍然很困难。所有算法都使用相同的一元术语,除了获得增强种子的随机游走(绿色)。第4列是单独从一元术语获得的分割。
边缘合作很自然地捕捉许多现有方法所忽略的信息,例如分割中的对象边界的全局特征。例如,考虑图1中的真空吸尘器(左):低对比度使得管难以识别,使得背景包括在前景中,或者部分管被切断。这种不正确的边界(因捷径而选择)与图案化地毯和真空吸尘器的正确边界有质的不同。我们认为边界是“一致的”:它是一个由少数相邻的纹理类型组成的重复模式,如果表示得当,可以帮助识别边界。通过将边界子分段在光照和阴影区域之间进行全局耦合,这种一致性可以被利用,这很容易通过Cooperative Cut来表达,如下所示。
更具体地说,我们展示:1)一类具有任意高阶的强大的能量函数,其势函数和最大阶数可以自动而有效地适应每个图像; 2)一种非常有效和实用的并且使用标准Graph Cut作为子程序的优化方法; 3)理论逼近保证了我们的优化方法; 4)一种特殊的边缘合作电势,与图形切割相比,将分割误差降低了高达70%。特别是对于具有严重缩小偏差问题的图像,对具有光强度梯度和阴影的图像以及同时具有这些困难的图像,我们有显着的改进。最后,我们将边缘合作与其他近期的计算机视觉方法联系起来。
第二节 背景:Graph Cuts和Gibbs Energies
在描述合作性削减之前,我们回顾一下Graph Cut和能量之间的关系,并且以此定义我们的符号。标记图像像素问题通常被定义为MRF中的推断问题。对于每个像素 在一个图像 ,一个随机变量从一个集合标签中取值。为了简单起见,我们只考虑二进制标签。Gibbs能量 在标签上 给定一个标签的观察像素值 ,定义概率为 。能量分解为一元潜能函数的总和,与图像相联系,和一个clique势能的总和 ,其中 是MRF中最大派系的集合。那就是
如 是恒定的,使用 简化符号。
通过找到最大后验概率(MAP)(等价地,能量最小化)变量分配来产生像素标记,i.e.,。 对于一个能量子系列,能量最小化相当于一个最小值 -cut在相应的图中[ 12 ]。一个关键的Graph Cut使能的成分是在成对情况下定义如下的“规律性”:对全部 ,我们有
在图的节点上,通过能量函数与集合函数之间的关系,自然地产生了Graph Cut。给定一个集合,每个像素一个元素,定义从标签到集合映射 。那么,能量 具有相应的集合函数 ,和规律性 相当于子模的 。 一个函数 如果全部是子模块的话,我们有 [ 9 ]。如果这个条件在所有的地方都是平等的话,那么被称为模块化(即, 对于一些 )。
代表成对的子模块能量 作为Graph Cut,定义加权有向图
有一个节点 对于每个图像像素,以及两个终端节点 。边缘 由像素间边缘组成 和终端边缘 。每个潜力 对应于两个边缘 ,每个单一的潜力 对应于边缘 (虽然这通常使用无向图来完成,但有向图更适合我们的需要)。最小的-cut 通过分配1来定义一个标签 ,如果 是从未切割 否则为0。同样,一个任务 定义一个 -cut入 。让 和 ,然后是一组定义切割的边缘。给定边权重,削减的成本 通常是权重的总和,这是边集的模块化功能。如果看作节点集合的函数,则这个削减成本是 ,这是一个众所周知的子模块功能 。 而且,对于成对的正则能量 存在一个 使得[ 23 ]
第三节 Cooperative Graph Cuts
边权重的模块化 在切割成本(3)中是一个关键的结构性限制:切割一条边对切割不同边的成本没有影响。模块化边权重允许高效的图形切割算法,但是也可能对计算机视觉结果具有有害的影响。
在我们的方法中,相反,切割边缘可能会影响切割其他边缘的成本。我们通过使用非递减的非负子模函数测量切割的成本来表达这种影响 定义在边的子集上 (与第2节截然不同,在子节点上定义子模块函数)。因为是子模和非负的,它也是次可加的: 。 如果不平等是严格的,我们会说 和 中的边是cooperate [ 30 ]。
节点之间合作切割的权重 和 可以表示为节点功能 。因此,合作的切割会导致一种形式的能量家族。这有三个后果。首先,MAP推断减少到最小合作切割。其次,根据在图中任意大的边集之间可以有协作。由于这耦合了所有的节点都与协作边缘相邻,具有任意高的阶数。第三, 不一定是规则的(相当于, 不一定是子模块的)。图2(a)显示了合作能量 违反规律(regularity)。 如果对于任何变量对的投影都是规则的话,那么更高的能量 是正规的[ 23 ]。让。投影 的 上 是通过固定值 到一些 来获得的 ,并设置 。
子模块功能可以奖励某些元素(这里是指图形切割的边缘)的共同出现。 有用的子模块功能包括(i) 为非负重 以及任何凹面,非降低功能 [ 30 ]; (ii)覆盖型功能,每个地方 有一个相关的集合或区域 ; (ⅲ)熵; 和(iv)在二部图中的邻域函数。而且,子模块功能的总和是子模块。图表结构可以获得额外的灵活性,如第5节和第6 节所示。
图2.(a)非规则能量的例子 同 。边缘权重如所示。如果尾部标签为1,标签为0,则切割边缘。考虑投影 对于 和 。然后,违反规律。(二)不同的影响在等式 (13)。
第四节 Optimization
尽量减少 ,我们必须解决一个最低Cooperative Cut。尽管耦合边缘允许 不正规的,这也使得NP难题:
定理1
最低Cooperative Cut是NP难的。
证明是从图形分割[ 17 ] 的减少。 另一方面,图结构提供了一个明确的优势超越一般高阶势,即对一些全局能量来说,没有任何算法可以为它找到的解决方案提供质量保证[ 5 ],[ 16]。相比之下,我们现在推导出一种实用且有效的Cooperative Cut近似算法,其具有近似保证。它迭代地最小化上限。
子模块函数的最简单的上界 是它的模块对应,但是这忽略了中所有的固有耦合 。相反,我们制定了一个很大程度保持合作的调整方案。定义 和一个边缘 中,边际成本的 关于 如 。子模块意味着边际成本递减: 对全部 。
引理1
对于子模块 ,和一个任意的 ,定义
功能 是一个模块化的上界 。
证明
对于任何集合 ,它认为[ 26 ]
边界(4)的边际成本递减:。模块化是直接的(立竿见影的)。□
这个界限增加了成本的上限 并减去成本的下限 。而且,这个边界是严格的,即,。
重要的是,cut cost 由于其模块化,可以有效地减少使用标准最小切割的次数。对于,定义 边缘权重
对于非递减,重量 是非负的。
引理2
在 上,最低 -cut是一个最小化的界限 。
与重量 ,削减的成本 是
由于 而且这个总和是固定的 对于任何边缘集合 。□
运用 ,我们推导出一个迭代最小化过程(算法1)。给定一个初始参考集,我们求出的最小割 。然后我们调整了这个束缚并重复。从而,在目前最好的解决方案中总是很严格。该算法从初始参考集开始,最简单的情况是 。为了进一步改进,其他选项包括集合 到一个cut基础的要素, 。,由生成树的cut边缘引起的切割。然而,对于第8节的实验, 是足够的,算法收敛在10次以内。
算法1:迭代界限最小化
作为引理2的结果,该算法在调整权重和计算最小切分之间交替。注意边缘的边际成本可以提高执行效率 只取决于配合的边缘 。重量 显示如何 捕捉到成本降低的效果 如果 合作 。对于模块化功能和算法1变为标准最小割。
引理3给出了初始解的一个逼近界 对于 ,这在随后的迭代中得到改进。
引理3
让 argmin an-cut} 是最小的cut对于 ,和 argmin an -cut}的最佳解决方案。让。然后
证明推迟到[ 16 ]。对于我们在第5节中使用的函数,术语总是非零,第二个不平等是严格的。引理3是一个最坏情况下的约束,并适用于任何非递减的子模块。在实践中,算法通常表现得更好[ 17 ]。
第五节 Structured cooperation for segmentation
我们现在将edge cooperation 应用于交互式图形 - 地面分割,其中,给定初始用户输入的情况下,其余像素将被标记为对象或背景。特别是,我们解决图1所示的问题:虽然这个任务,Graph cut算法已被成功地用于此,但是它们却被认为是快捷延伸的边界,特别是在低对比度,阴影区域(也参见图3。 ,4,5)。这些问题是由标准的网格结构MRF固有的成对能量所导致的:
关联的图表 有终端边缘 ,以及像素间边缘的网格 表达成对的潜力。前者整合用户交互,后者则强化平滑性和一致性。边上的权重是强度梯度的函数; 他们的总和可能被视为边界的加权长度。这个惩罚有利于简短的界限,从而导致上述的简化。降低系数并不是解决方案,因为边界变得嘈杂,真实的背景被包含在假设的前景中(图5)。
相反,我们利用edge cooperation 有选择性地奖励真实边界的全局特征。具体来说,我们保留并且只用一个Cooperative Cut替换过度平滑的像素
由于在中,物体边界由切边构成,因此我们需要一个包含理想边界特征的子模边成本。我们观察到,在真实的物体边界上,许多图像具有一定的一致性,这在整个图像中可能是真实的。边界一致性在许多上下文中具体化。例如,在图3,5中许多像素间的颜色梯度中,只有少数几个出现在困难区域中是沿着真实的边界的; 而裁剪则引入了新的不协调的边界类型。此外,图案背景的重复在很大程度上也保持了一致性。类似地,如果阴影被中和,则图1中的照明区域和阴影区域之间具有一致性。在后一种情况下,我们需要一个阴影不变的一致性标准。
所以, 应该:(i)减少对全局一致边界的惩罚,(ii)保持不一致边界的成对潜力的共同平滑效果,以及(iii)允许对每个图像自动和有效地适配一致性准则。
我们用类似的边界类来定义一致性, 和 。一致的边界使用几个类。子模块可以有选择地奖励一致性,因为它具有递减的边际成本。但是,我们只能在类内部使模块化,而不能跨模块化:
结果,(i)边缘的边际成本仅在来自同一类的足够的边缘被cut时才会降低。折扣随着该类别包含的边缘数目而增加。另一方面,(ii)对于使用多个类别的边缘的裁剪没有折扣,即,不协调的裁剪。类成本是阈值折扣函数,
对于任何非递减的非负凹函数 。对于我们的实验,我们选择了。可替代的选择包括或根 (图2(b))。模块化外壳(9)对应于。
为了适应 ,我们通过聚类的边缘来推断每个图像的类别。此外,折扣只能在到达了门槛之后 设置,我们将 应用到类的总权重中,即, 对于 [0],[ 1 ],这提高了尺度不变性。对于大型物体或图像,在一个类中有更多的边,需要更多的切割来观察折扣。因素 在完全模块化cut 和完全合作削减 之间进行交换。
“一致性”的定量标准取决于用来聚类边缘的距离度量。对于具有观察像素值 的边 ,我们定义了两个可能的特征向量 :(i)对于均匀照明的图像,我们使用线性颜色梯度, ,和平方欧几里德距离进行聚类; 和(ii)对于阴影,我们使用对数强度比 (彩色图像通道),这对于阴影是近似不变的,以及聚类的 距离。在不同的情况下,我们使用特征,或者 用于聚类边缘,并使用标准权重 代替 。
表格1。EXAMPLES OF COOPERATIVE CUTS; 是边缘的标签 [ 16 ],RIDTHE小号的UM(平方) w ^ 八分。
第六节 The expressive power of cooperative cuts
Cooperative cuts涵盖了(并严格概括了)计算机视觉领域的一些最新方法(总结在表1中)。但是请注意,Cooperative cuts并不是任何这些方法的特例(例如,有些不是NP-hard)。
Kohli 等人 [ 19 ]考虑 形式的电势 为一个凹,非衰减的函数 和集团 。因为他们的结构在二进制情况下,成对电势 的和可以描述图中的切割。与图2中的例子不同,这些电势是Cooperative cuts的特殊情况[ 19 ] 。 同样的, 多标签 的 交换是一个合作的cut,如果 是一个度量,那么扩展 [ 16 ]。 该 (potts)模型[ 19 ]和鲁棒性电势[ 20 ]都是cooperative cut的常规特例[ 16 ]。
在基于类的图像分割中,每个像素必须由被一个对象类标记。Ladický 等人 [ 25 ]提出了一个全局性的电势 在一组类标签上 用于 。 如果 是不减少和子模块,然后 扩张可以表述为cooperative cut [ 16 ]。 共现函数 在[ 25 ]中不是关于类标签的子模块。一个替代方案,子模块 可以计算标签不包含整个集合的训练图像的数量 。 在[ 6 ]中的 label-cost 函数是子模块,因此是在上的合作的切割,因为它对应于双向图中的邻域函数[ 16 ]。
最后,Sinop和Grady [ 31 ]将Random Walker算法的变体[ 11 ] 表示为目标。在离散版本中, 如果且仅当边 被切断。由于第q根是凹的,是子模块。这同样适用于 版 。因此,[ 31 ] 的离散情况也是合作切入。
第七节 Other related work
从[ 12 ]开始,graph cuts已经成为计算机视觉的标准,有许多应用[ 2 ],[ 3 ],[ 4 ],[ 14],[ 13 ]。 在标准情况下,切割代表成对的,常规的能量,但graph cuts也可以用于非子模块成对的电位[ 22 ]和比率问题[ 21 ]。
除了成对能量之外,有效优化的高阶势能已经成为许多近期研究的主题([ 15 ],[ 18 ],[ 24 ]和其中的参考文献),但是这些电势的结构与边缘合作有很大的不同。 高阶约束的例子包括单一的全局约束,如连通性[ 27 ],统计约束[ 25 ],或强化同质性的节点组[ 19]。虽然用户交互连接已经被用来解决缩小的偏见[ 32 ],但是对于树木可能会变得乏味(图5),并且没有处理洞(图4)。
第八节 Experiments
对于交互式图形 - 地面分割的任务,我们的实验解决了三个主要问题:(i)耦合边缘的影响是什么,这是否强化了正确的边界?我们比较(CoopCut)从第5节到标准图切割(GC)[ 2 ]成对电位。(ii)耦合结构(即类)的作用是什么?(iii)边缘合作是否损害了需要标准平滑的对象的分割?
我们使用彩色和灰度图像的复杂对象,有和没有阴影。因为据我们所知,这样的图像没有公共数据库,所以我们创建了自己的手标记集合。图片和代码可在ssli.ee.washington.edu/~jegelka/cc找到。 对于(iii),我们使用Grabcut数据[ 1 ],[ 28 ]。
两种方法使用相同的8邻居图结构,相同的一元电位和像素间的边权重 边缘 和方差 的颜色渐变(参数在[ 32 ])。 一元电位可以基于颜色直方图[ 2 ],也可以基于高斯混合模型(GMMs)和5个元素[ 28 ],[ 32 ]。边类是由k均值聚类推断的,相同颜色的像素之间的边形成一个额外的类 没有折扣 。错误是错误分配的未标记像素的百分比。为了量化只占像素一小部分的精细目标部分的回收率,我们只计算这些精细部分的“树枝误差”。我们为每种方法选择了好的参数。在表2,3,参数上的所有图像是相同的。所有的算法都是用C ++实现的,使用图形切割代码[ 3 ],OpenCV和一些Matlab预处理。有关详细信息和更多结果,请参见[ 16 ]。
结果表明:(1)合作有助于追踪阴影区域的边界,并保留细分; (二)重要的是合作的结构; (iii)对复杂边界的改进不会损害“标准”边界的结果。
实验1
阴影渐变表2显示了在(a)8个灰度和(b)7个彩色图像中的阴影对象上的分割错误。在这样的图像中,一元术语是非常嘈杂(图1,3)。耦合边缘使用与GC相比,误差减少了三分之二。图3和图4显示CoopCut更好地恢复目标形状。为了确保不仅仅是比率信息而是合作产生了差异,我们运行了GC(“log”)的边权值:错误只会稍微改善。为了探究类的效果,我们比较了一下cooperative cut,只与一个类(加上类)进行比较 。这种统一的,非结构化的耦合效果要差得多,也就是说, 是至关重要的。
CoopCut不会明确地建模阴影,而是通过删除阴影效果 。因此,如果阴影局部随较高的频率变化而变化,则也会改善结果。我们通过乘以像素的位置乘以0.4 ,来人为地遮蔽来自Expt。2,。从修改后的图像中计算出一元术语。图4显示了一个例子,表2列出了18个这样的图像的平均错误。事实上,CoopCut减少了GC的总误差,保留了比GC更好的微妙结构。
实验2
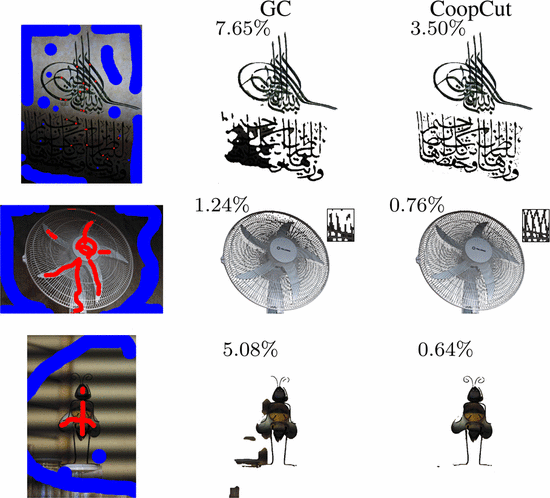
细长的零件和孔。为了检查在均匀照明的图像中耦合的效果,我们计算17个具有微妙物体的图像的总体和枝条误差。表2(d)和图5显示了两个参数设置的结果:(1)总体误差较小,(2)枝条误差较小。如果平滑项被减少,图切割粗略地恢复了精细结构,但是以高总体分割误差为代价。CoopCut保留精美的部分,不包括背景。总和树枝误差同时被最小化。 相比之下,曲率正则化(如[ 7 ]中的一元项)对一元项中的噪声更敏感([ 7],[ 29 ] 中的较少噪声)。
实验3
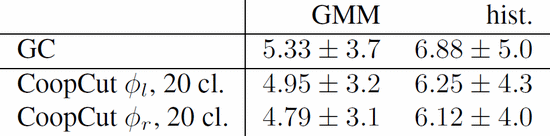
Grabcut数据。作为一个“健全检查”,我们处理合作的效果与对象较为圆润,需要正规化。表3显示了Grabcut数据集[ 1 ],[ 28 ] 的50幅带有“Lasso”标签的图像上的GC和CoopCut的误差。即使在这里,CoopCut也会在两种颜色模型上稍微提高结果。图3显示了GC面向收缩偏差的两个对象的分割,CoopCut恢复形状。
最佳的参数选择随着设置而略有变化,就像使用标准图形切割一样,但是这些误差表明对于大范围的图像来说一个选择是合理的。
图3.示例的结果和错误 1(左)和Grabcut数据(右)。GC具有最小误差参数; CoopCut在两个图像上。抓取数据:GC,CoopCut(15和10班):
图4. 15,20和25类的阴影彩色图像的结果(从上到下)为低总量和枝条误差选择参数; GC:;。CoopCut:放大显示了网格的一部分。
图5.实施例结果实验2。合作保留腿和细枝,不包括背景(箭头)。参数:GC低错误。,GC低 ; CURV。,CoopCut:
表2.对于E XPT的VEROR E RROR(百分比 M ISPREDICTED像素)。1和2。ģ Ç:ģ RAPH Ç UT,C OOPCUT:C OOPERATIVE Ç UT W¯¯ ITH 1-20 Ç LASSES。(A),(B) Ť OTAL AND ë RROR(2ERRTOTAL±ERRTWIG) 。甲CROSS 8和7我MAGES; (C),(d) Ť OTAL AND Ť WIG ë RROR(2ERRTOTAL±ERRTWIG) 。一个十字架18和17 I MAGES,RESPECTIVELY; (C),(d) - [R ESULTS FOR P ARAMETERS W¯¯ ITH (1)中号的最小值 Ť OTAL AND ë RROR,AND (2)中号的最小值 Ĵ OINT ë RROR(2ERRTOTAL±ERRTWIG) 。Ç OOPCUT甲CHIEVES大号OW Ť OTAL AND Ť WIG ë RROR,W HEREAS GC Ç AN ö NLY中号INIMIZE ö NE的 Ť 软管。T WIG ERROR IS Ø VERALL ^ h IGHER小号因斯IT Ç OUNTS ˚F 壶 P IXELS。ř ESULTS WITH ħ ISTOGRAM ù 进制 Ť ERMS ARE小号IMILAR [ 16 ]。
表3 é RRORS ON THE ģ RABCUT d WITH ATA乙OTH ˚F EATURE Ť YPES。
第九节 Discussion
我们引入了一个通用模型,合作削减,可以表达一个全局电势家族和奖励共现,同时仍然是有效近似。我们证明了它对图像分割的有效性,在这里我们奖励局部边界特征的共现。这是一个新型的类结构合作,推动全局削减相似的边缘,而不是仅仅几个边缘。因此,我们的方法可以被看作是一个离散的结构化的稀疏性。此外,它可以扩展到多个标签。交换或扩大动作,然后成为合作削减。最后,与其他近期模型的关系意味着分割只是合作切割的丰富建模能力的一种可能的应用。卡普为“合作切”的名称。
一个CKNOWLEDGMENTS
感谢Sebastian Nowozin,Peter Gehler和Christoph Lampert的评论,以及Richard Karp的合作。










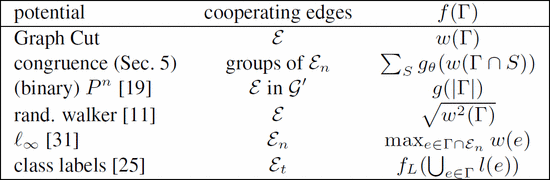
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








