数据结构——动态规划

数据结构——动态规划

---

---

前言

动态规划（英语：Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

---

一、动态规划是什么？

简单来说，动态规划其实是一种算法思想：若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

应用这种算法思想解决问题的可行性，对子问题与原问题的关系，以及子问题之间的关系这两方面有一些要求，它们分别对应了最优子结构和重复子问题。

最优子结构

最优子结构规定的是子问题与原问题的关系

动态规划要解决的都是一些问题的最优解，即从很多解决问题的方案中找到最优的一个。当我们在求一个问题最优解的时候，如果可以把这个问题分解成多个子问题，然后递归地找到每个子问题的最优解，最后通过一定的数学方法对各个子问题的最优解进行组合得出最终的结果。总结来说就是一个问题的最优解是由它的各个子问题的最优解决定的。

重复子问题

重复子问题规定的是子问题与子问题的关系。

当我们在递归地寻找每个子问题的最优解的时候，有可能会重复地遇到一些更小的子问题，而且这些子问题会重叠地出现在子问题里，出现这样的情况，会有很多重复的计算，动态规划可以保证每个重叠的子问题只会被求解一次。当重复的问题很多的时候，动态规划可以减少很多重复的计算。

重复子问题不是保证解的正确性必须的，但是如果递归求解子问题时，没有出现重复子问题，则没有必要用动态规划，直接普通的递归就可以了。

例如，斐波那契问题的状态转移方程 f(n) = f(n - 1) + f(n - 2)。在求 f(5) 时，需要先求子问题 f(4)和 f(3)，得到结果后再组合成原问题 f(5) 的解。递归地求 f(4) 时，又要先求子问题 f(3)和 f(2) ，这里的 f(3) 与求 f(5)时的子问题重复了。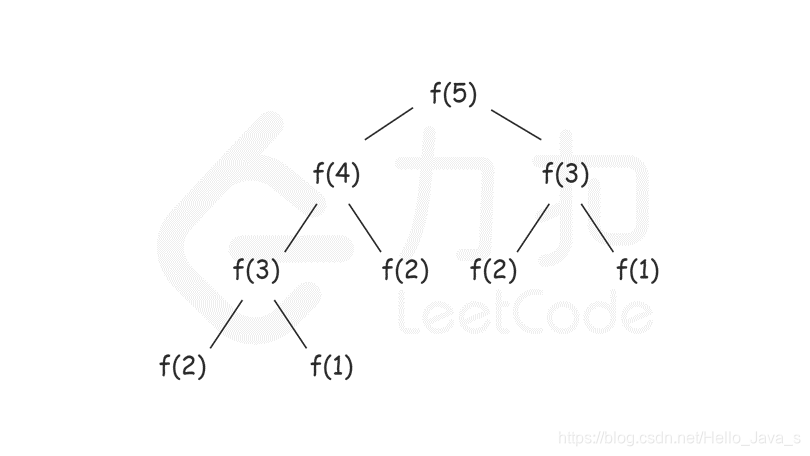
解决动态规划问题的核心：找出子问题及其子问题与原问题的关系

找到了子问题以及子问题与原问题的关系，就可以递归地求解子问题了。但重叠的子问题使得直接递归会有很多重复计算，于是就想到记忆化递归法：若能事先确定子问题的范围就可以建表存储子问题的答案。

动态规划算法中关于最优子结构和重复子问题的理解的关键点：

• 证明问题的方案中包含一种选择，选择之后留下一个或多个子问题
• 设计子问题的递归描述方式
• 证明对原问题的最优解包括了对所有子问题的最优解
• 证明子问题是重叠的（这一步不是动态规划正确性必需的，但是如果子问题无重叠，则效率与一般递归是相同的）

二、示例

1.最长上升子序

Leecode链接：https://leetcode-cn.com/problems/longest-increasing-subsequence/

题目：300.最长上升子序列

描述：给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例：
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是4。

考虑能否将问题规模减小

将问题规模减小的方式有很多种，一些典型的减小方式是动态规划分类的依据，例如线性，区间，树形等。这里考虑数组上常用的两种思路：

每次减少一半：如果每次将问题规模减少一半，原问题有[10,9,2,5]，和[3,7,101,18]，两个子问题的最优解分别为 [2,5] 和 [3,7,101]，但是找不到好的组合方式将两个子问题最优解组合为原问题最优解 [2,5,7,101]。

每次减少一个：记 f(n)为以第 n个数结尾的最长子序列，每次减少一个，将原问题分为 f(n-1), f(n-2), …, f(1)，共 n - 1 个子问题。n - 1 = 7 个子问题以及答案如下：

[10, 9, 2, 5, 3, 7, 101] -> [2, 5, 7, 101]
[10, 9, 2, 5, 3, 7] -> [2, 5, 7]
[10, 9, 2, 5, 3] -> [2, 3]
[10, 9, 2, 5] -> [2, 5]
[10, 9, 2] -> [2]
[10, 9] -> [9]
[10] -> [10]

已经有 7 个子问题的最优解之后，可以发现一种组合方式得到原问题的最优解：f(6)的结果 [2,5,7], 7 < 18，同时长度也是 f(1)~f(7)中，结尾小于 18 的结果中最长的。f(7)虽然长度为 4 比 f(6) 长，但结尾是不小于 18 的，无法组合成原问题的解。

以上组合方式可以写成一个式子，即状态转移方程

f(n) = max{f(i)} + 1 其中 i < n 且 a[i] < a[n]

这种思考如何通过 f(1)…f(n-1) 求出 f(n) 的过程实际就是在思考状态转移方程怎么写。

总结： 解决动态规划问题最难的地方有两点：

1. 如何定义 f(n)
2. 如何通过 f(1), f(2), … f(n - 1) 推导出 f(n)，即状态转移方程

递归

有了状态转移方程，实际上已经可以直接用递归进行实现了。
代码如下：

int f(vector<int>& nums, int i)
{
    int a = 1;
    for(int j = 0; j < i; ++j)
    {
        if(nums[j] < nums[i])
        ¦   a = max(a, f(nums, j) + 1);
    }
    return a;
}

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/dynamic-programming-1-plus/xcos8s/
来源：力扣（LeetCode）

自顶向下（记忆化）

递归的解法需要非常多的重复计算，如果有一种办法能避免这些重复计算，可以节省大量计算时间。记忆化就是基于这个思路的算法。在递归地求解子问题 f(1), f(2)… 过程中，将结果保存到一个表里，在后续求解子问题中如果遇到求过结果的子问题，直接查表去得到答案而不计算。
代码如下：

int f(vector<int>& nums, int i, vector<int>& dp)
{
    if(dp[i] != -1) return dp[i];
    int a = 1;
    for(int j = 0; j < i; ++j)
    {
        if(nums[j] < nums[i])
        ¦   a = max(a, f(nums, j) + 1);
    }
    dp[i] = a;
    return dp[i];
}

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/dynamic-programming-1-plus/xcos8s/
来源：力扣（LeetCode）

对于这种将问题规模不断减少的做法，我们把它称为自顶向下的方法。

转载声明

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/dynamic-programming-1-plus/xcos8s/
来源：力扣（LeetCode）