目录
一.堆的概念以及性质
1.什么是堆?
堆通常是一个可以被看做一棵完全二叉树的数组对象。
2.堆有什么性质?
堆总是满足下列性质:堆中某个节点的值总是不大于或不小于其父节点的值,堆总是一棵完全二叉树。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
说白了,只要是堆,那么这个堆不是大堆就是小堆。
每个父节点都大于子节点 --- 大堆
每个父节点都小于子节点 --- 小堆
3.堆的逻辑结构与存储结构示意图
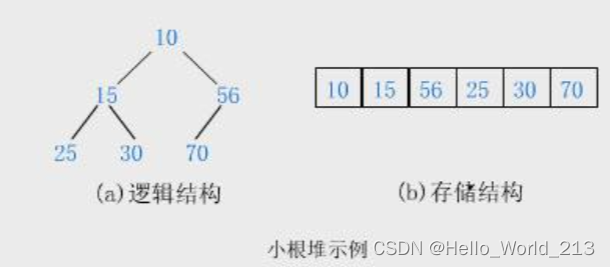
二.堆的实现(以构建小堆为例)
在这之前先说明一下,假设我们用parent、leftchild、rightchild表示父节点、左子节点、右子节点下标
这三者之间的关系:parent = (child - 1) / 2
leftchild = parent * 2 + 1
rightchild = parent * 2 + 2
堆的高度为h,总节点个数为N。关系为 N = 2^h - 1
堆的结构体:
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;初始化:
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
1.堆的向下调整算法
(1)思想
随机给定一个数组,用给定数组表示出一个完全二叉树结构。
从根节点出发,依次向下调整,将其调整为一个堆结构。
使用向下调整算法的一个前提:左右子树必须也都是小堆。
分治思想:大事化小,将问题分解成n个子问题,n个子问题分解成n个子问题的子问题。
时间复杂度:O(logN)
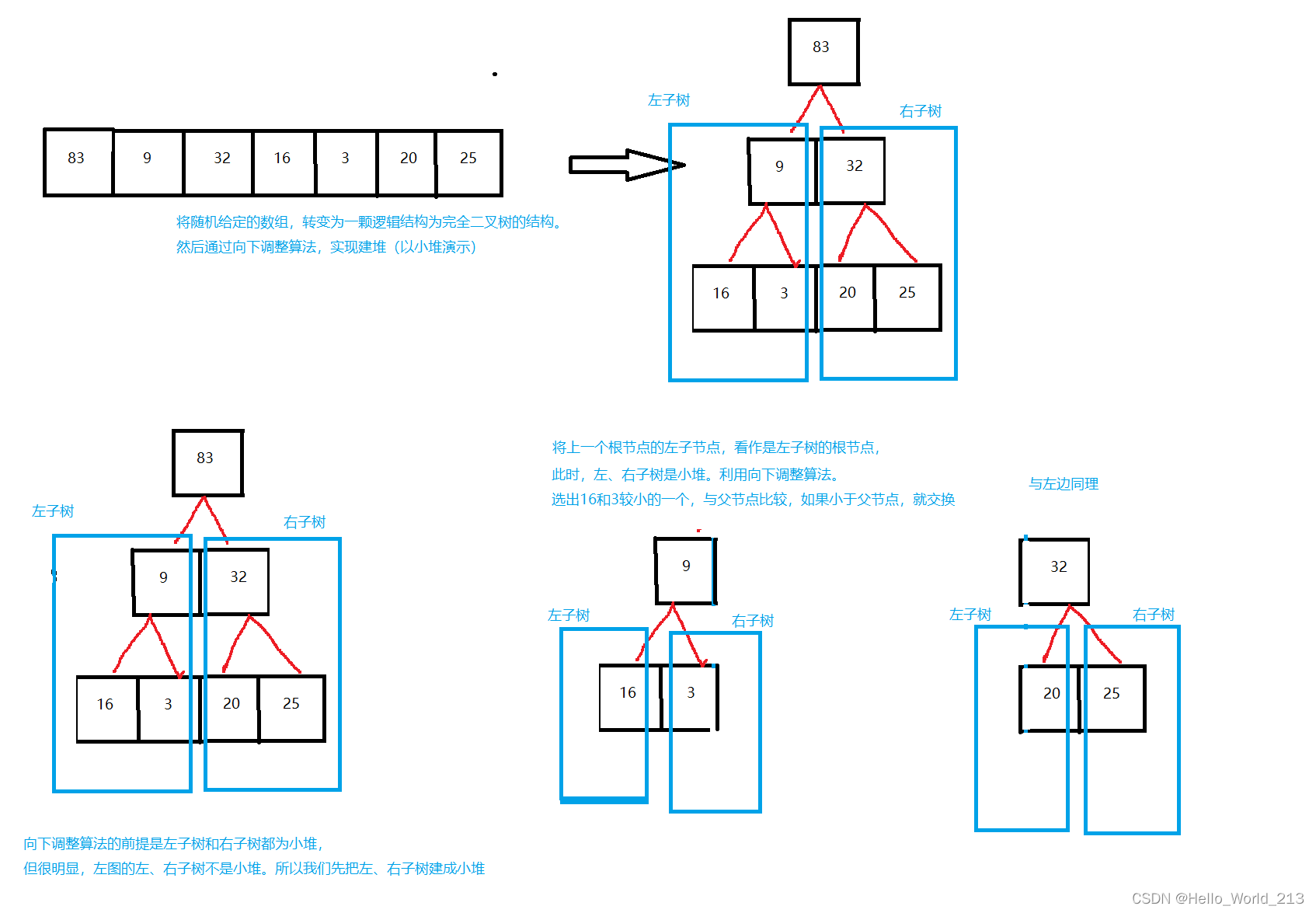
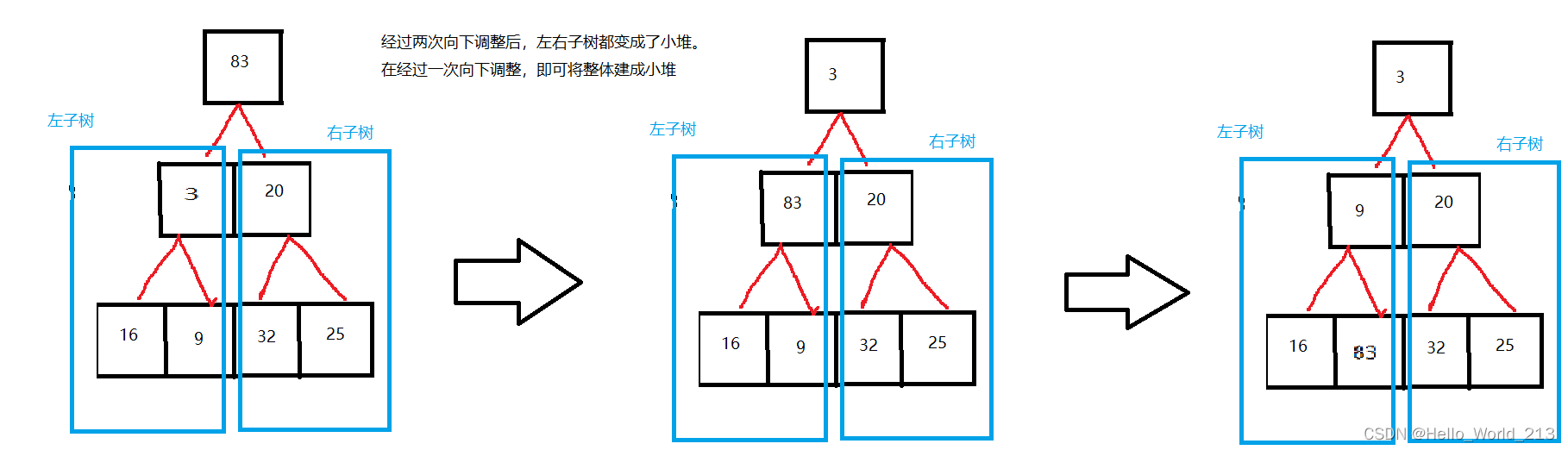
值得注意的是:我们这里给的物理存储结构是数组!!!完全二叉树只是一种逻辑结构!!!
(2)向下调整算法的两种代码实现
迭代:
void AdjustDown1(HPDataType* a, int size, int parent)
{
assert(a);
//默认左孩子最小
int child = parent * 2 + 1;
while (child < size)
{
//如果右孩子比做孩子小,就修正
if (child + 1 < size && a[child + 1] < a[child])
{
child++;
}
//最小的孩子比父亲小,就叫唤
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
//交换后,把孩子的身份变为父亲
parent = child;
child = parent * 2 + 1;
}
else
{
//调整完成了,跳出循环
break;
}
}
}递归:
void AdjustDown2(HPDataType* a, int size, int parent)
{
//默认左孩子最小
int child = parent * 2 + 1;
if (child >= size)
{
return;
}
//如果右孩子比做孩子小,就修正
if (child + 1 < size && a[child + 1] < a[child])
{
child++;
}
//最小的孩子比父亲小,就叫唤
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
}
else
{
return;
}
AdjustDown2(a, size, child);
}2.堆的向上调整算法
(1)思想
思想整体和向下调整算法类似,只不过是自下至上。
以建小堆为例,直接与父亲节点比较,如果小于父亲节点就交换,向上调整算法不用考虑子问题,直接交换即可。
时间复杂度O(logN)
(2)向上调整算法的代码实现
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)//这里千万不要用parent>=0做为循环条件,否则就是给自己挖了一个大坑!
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;//因为一个负数除以2得0,如果parent>=0做循环条件,则死循环
}
else
{
break;
}
}
}3.堆的插入(尾插)
在堆的数组的最后插入,然后在进行一次向上调整。
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
//判断是否需要扩容
if (hp->_capacity == hp->_size)
{
//给定新容量
int Newcapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * Newcapacity);
if (tmp == NULL)
{
printf("realloc failed\n");
exit(0);
}
hp->_a = tmp;
hp->_capacity = Newcapacity;
}
//直接在末尾插入
hp->_a[hp->_size] = x;
hp->_size++;
//向上调整算法
AdjustUp(hp->_a, hp->_size - 1);
}4.建堆
(1)向上调整建堆法
从下标为0的位置,依次将数组中的元素插入到堆中,每次都执行向上调整算法
时间复杂度:O(N*logN)
向上调整建堆法的代码实现
void HeapCreateUp(HPDataType* a, int n)
{
for (int i = 0; i < n; i++)
{
AdjustUp(a, i);
}
}(2)向下调整建堆法
从数组的最后一个元素的父节点开始,执行向下调整建堆。
原因就是:向下调整法的一个前提就是左右子树都必须是堆。
时间复杂度:O(N)
那么这是应该就会有人问了,遍历n次,每次向下调整是logN,时间复杂度不应该是O(N*logN)吗?
答案是:错了!用数学公式推导即可知晓!
向下调整建堆法的代码实现
void HeapCreateDown(HPDataType* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)//n-1是最后一个元素的下标
{
AdjustDown1(a, n, i);
}
}(3)向下调整建堆法的时间复杂度推导
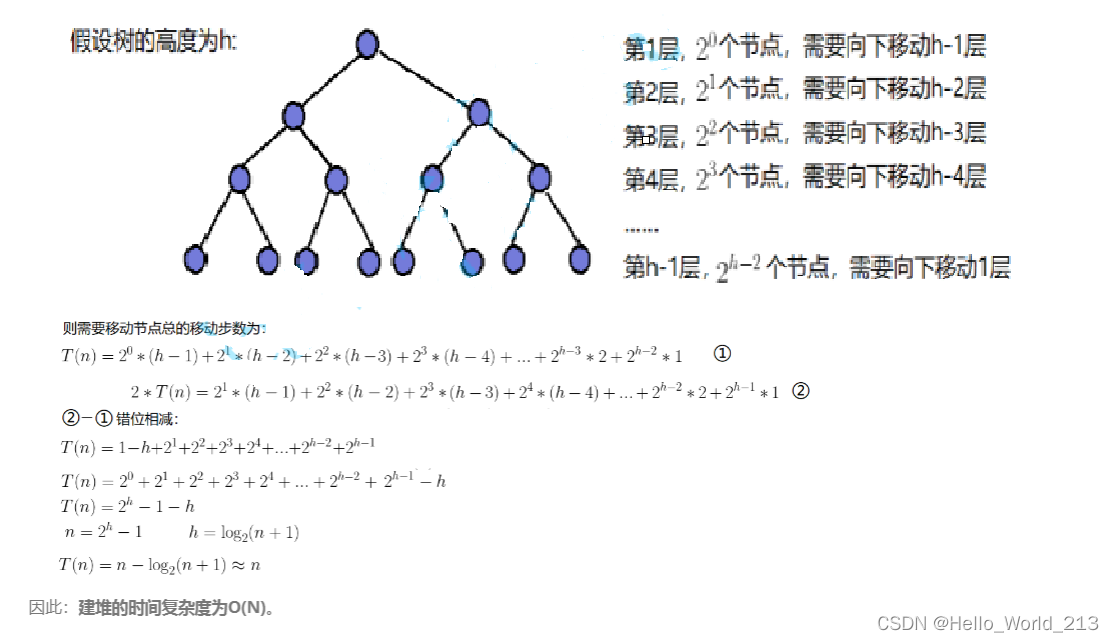
5.堆的删除(删堆顶)
将堆顶与最后一个元素互换,尾删,再向下调整
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown1(hp->_a, hp->_size, 0);
}6.堆的其他基础操作
(1)取堆顶的数据
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
return hp->_a[0];
}
(2)堆的数据个数
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
(3)堆的判空
// 堆的判空
bool HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0;
}
(4)堆的销毁
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->_a);
hp->_capacity = hp->_size = 0;
}三.堆排序
1.基于堆数据结构的堆排序(以排升序为例)
这种堆排序相较最优的堆排序而言,需要使用到堆的数据结构,以及堆的一系列基础操作,且空间复杂度较高
时间复杂度:O(N*logN)
空间复杂度:O(N)
排升序 --- 建小堆
排降序 --- 建大堆
void HeapSort1(Heap* hp, HPDataType* a, int n)
{
assert(hp);
//先把数组中的元素依次插入到堆中,建成小堆
for (int i = 0; i < n; i++)
{
HeapPush(hp, a[i]);
}
//依次将堆顶数据按顺序放入数组中
int i = 0;
while (!HeapEmpty(hp))
{
a[i++] = HeapTop(hp);
HeapPop(hp);
}
}2.最优的堆排序(以排降序为例)
不需要借助堆的数据结构,在原数组直接排序,但应用堆的思想
时间复杂度:O(N*logN)
空间复杂度:O(1)
排升序 --- 建大堆
排降序 --- 建小堆
//排降序一定要建小堆,建小堆堆顶数据就是最小的,将堆顶和最后元素交换后最后的元素就是最小的,
//将最后一个元素忽略掉,在重新建堆,只需要一次向下调整即可。这样依次把最小、次小的放在堆的最后。
//如果建大堆堆顶元素是最大的,把堆顶忽略掉,重新建堆时间复杂度是O(N)这时堆的结构就全乱了
void HeapSort2(HPDataType* a, int n)
{
assert(a);
//建小堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown1(a, n, i);
}
int end = n - 1;
while (end > 0)
{
//交换首尾元素
Swap(&a[0], &a[end]);
//向下调整重新建成小堆
AdjustDown1(a, end, 0);
end--;
}
}四.topK问题(在N个数中找最大的前K个数)
1.简述 -- 什么是topK问题?
比如:未央区排名前10的泡馍,西安交通大学王者荣耀排名前10的韩信,全国排名前10的李白。等等问题都是Topk问题,
总而言之,就是要在N个数据中,找出前K名,这就是典型的topK问题。对于topK问题而言,堆,是最优解决方案!
在这里我们研究在N个数中找最大的前K个数
2.为什么用堆解决topK问题?
(1)如果N个数内存可以放下
1.排序 --- 时间复杂度:O(N * logN)
2.对N个数建堆,top/pop K次 --- 时间复杂度:O(N + K * logN)
显然堆结构相比于排序而言更优。
(2)如果N个数内存放不下
在N个数中找最大的前K个数
数据总数是N,假设N是一内存无法一次性存储的巨大的数。我们无法将数据全部存储到内存中用快排等等算法进行排序。
使用排序可以吗?
因为前提是内存放不下N个数,将部分数据快排之后再把新的数据与最小或者最大的作比较,满足条件之后再进行一次快排。
这样是及其低效的,遍历N-K个数据的时间复杂度是O(N),一次排序的时间复杂度是O(N*logN),整体时间复杂度就是O(N^2*logN)!
最合理的解决方法:堆
1.找出N个数据中的K个数建小堆
2.让剩余的N - K个数与堆顶比较,符合条件就进堆。
这样遍历结束之后,结果就是,最后的堆中的数据,就是我们要选出的K个数。
这里必须建小堆,让堆顶最小,才能让比这K个数大的数进堆。
时间复杂度:O(K + (N - K) * logK)
3.代码实现用 数据结构 - 堆 解决topK问题
这里使用1w个数据选10个最大的数,来模拟topK问题
void PrintTopK(int* a, int n, int k)
{
assert(a);
int* Array = (int*)malloc(sizeof(int) * k);
assert(Array);
for (int i = 0; i < k; i++)
{
Array[i] = a[i];
}
//1.将前k个数建小堆。
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown1(Array, k, i);
}
//2.遍历
for (int i = 0; i < n; i++)
{
//与堆顶比较,大于堆顶就替换
if (a[i] > Array[0])
{
Array[0] = a[i];
}
//向下调整成小堆
AdjustDown1(Array, k, 0);
}
//打印
for (int i = 0; i < k; i++)
{
printf("%d ", Array[i]);
}
printf("\n");
}
//模拟topK问题
void TestTopK()
{
int n = 10000;
int* arr = (int*)malloc(sizeof(int) * n);
assert(arr);
//随机给10000个数据
srand((unsigned int)time(NULL));
for (int i = 0; i < n; i++)
{
arr[i] = rand() % 10000;
}
//题目:在10000个数中,选出前10个最大的数
int k = 10;
//定义10个最大的数
arr[5400] = 10000 + 4;
arr[44] = 10000 + 8;
arr[999] = 10000 + 6;
arr[523] = 10000 + 9;
arr[320] = 10000 + 18;
arr[823] = 10000 + 42;
arr[3942] = 10000 + 9;
arr[2341] = 10000 + 1;
arr[452] = 10000 + 2;
arr[9149] = 10000 + 3;
//打印出这10个最大的数
PrintTopK(arr, n, k);
}





















 1279
1279











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








