复活小记？

哇，我复活啦

高考炸了，低于100分的数学让我被迫苟近了中大
然后就被“邀请”去参加acm选拔赛了。
康复训练效果感觉不佳啊，tarjan都快忘了，更别提什么网络流min25多项式之类的了。
靠着切切水题混着看了。

复习了一下杜教筛，就拿这个来当个重启的契机吧。
原博客地址

补充几个小小的有用的性质：

$1、\mu \ast I=ϵ$
$2、\phi \ast I=id$
$3、\mu \ast id=\phi$
$4、{\sum }_{d|n}\frac{\mu (d)}{d}=\frac{\phi (n)}{n}$

证明：
$1、\mu \ast I={\sum }_{d|n}\mu (d)$
那么如果n不为1，那么必然可以分为多个不同的质因数。
然后观察$\mu$的计算公式：

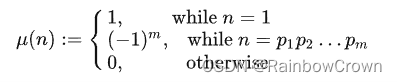
那么$m=1、2、3、4\dots$时，那么不就是组合数中的交替正负号然后求和吗。
于是乎就可以知道只有当$n=1$时原式等于1，其余都为0。

$2、\phi \ast I={\sum }_{d|n}\phi (d)$
$\phi (n)$的意义是1到n-1中与n互质的数的个数。
首先我们看当$n=p^q（p为某质数）$时会发生什么：
${\sum }_{d|n}\phi (d)=\phi (1)+\phi (p)+\phi (p^2)+\dots +\phi (p^q)$
$=1+(p-1)+(p^2-p)+\dots \dots +(p^q-p^{q-1})=p^q$
然后如果$n=\Pi p_i^{q_i}$
那么由于$\phi (n)$是积性函数，根据狄利克雷卷积性质，那么$\phi (n)\ast I$也是积性函数，那么我们就可以分成：
$(\phi \ast I)(\Pi p_i^{q_i})=\Pi (\phi \ast I)(p_i^{q_i})$
那么就和上面的同理了。

$3、\mu \ast id={\sum }_{d|n}\mu (d)\ast \frac{n}{d}$
当n为质数时，那么 $原式=\mu (1)\ast n+\mu (n)\ast 1=n-1=\phi (n)$
如果n可以表达成：$n=p^q$，那么 $原式=\mu (1)\ast n+\mu (p)\ast p^{q-1}+\dots +\mu (p^q)\ast 1$
可以发现中间的项都为0。于是原式化简为：$\mu (1)\ast n+\mu (p)\ast p^{q-1}=n-p^{q-1}=\phi (n)$
如果n可以表达成：$n=\Pi p_i^{q_i}$那么类似于第二条性质一样，拆开即可。

$4、{\sum }_{d|n}\frac{\mu (d)}{d}=\frac{\phi (n)}{n}$
两边同时乘一个n试试？

关于单位元

由于之前并没有仔细研究单位元。
又看到$ϵ(n)=[n==1]$被称为狄利克雷卷积的单位元。
小证一下？
$(f\ast ϵ)(n)={\sum }_{d|n}f(d)\ast ϵ(\frac{n}{d})=f(n)$
挺显然的
有什么用呢？

关于逆元

既然我们知道了$f(n)$的单位元是$ϵ(n)$
那么我们可以找到一个函数$g(n)$使得：
$(f\ast g)(n)=ϵ(n)$
那么这个$g(n)$便是$f(n)$的逆元。
怎么找呢？
$(f\ast g)(1)={\sum }_{d|1}f(d)\ast g(\frac{1}{d})=f(1)\ast g(1)=1$
那么按理来讲，我们可以直接令$g(1)=\frac{1}{f(1)}$
其他呢？
$(f\ast g)(2)={\sum }_{d|2}f(d)\ast g(\frac{2}{d})=f(1)\ast g(2)+f(2)\ast g(1)=f(1)\ast g(2)+\frac{f(2)}{f(1)}=0$
那么$g(2)=-\frac{f(2)}{(f(1){)}^2}$
同理：
$(f\ast g)(3)={\sum }_{d|3}f(d)\ast g(\frac{3}{d})=f(1)\ast g(3)+f(3)\ast g(1)=f(1)\ast g(3)+\frac{f(3)}{f(1)}=0$
$g(3)=-\frac{f(3)}{(f(1){)}^2}$

$(f\ast g)(4)={\sum }_{d|4}f(d)\ast g(\frac{4}{d})=f(1)\ast g(4)+f(2)\ast g(2)+f(4)\ast g(1)=f(1)\ast g(4)-\frac{(f(2){)}^2}{(f(1){)}^2}+\frac{f(4)}{f(1)}=0$
$g(4)=-\frac{f(4)}{(f(1){)}^2}+\frac{(f(2){)}^2}{(f(1){)}^3}$

归根结底来看，我们可以总结为这条式子：
$$g(n)=\{\begin{array}{ll}\frac{1}{f(1)}& n=1\\ -\frac{1}{f(1)}\ast {\sum }_{d|nd!=1}f(d)\ast g(\frac{n}{d})& n>1\end{array}$$
其中还能发现：只有$f(1)$不为0时有其逆元。

有什么用？