深度学习中需要的矩阵计算
The Matrix Calculus You Need For Deep Learning
翻译自: explained.ai
原作者: Terence Parr and Jeremy Howard我只翻译了主要的几个部分。翻译有问题请联系我 lih627@outlook.com
摘要
这篇文章的目的是为了解释深度神经网络训练过程中的矩阵运算。目的是帮助对了解基本神经网络的人加深对其中数学知识的理解。文章末尾提供参考文献总结了文章中讨论的矩阵运算法则。同时可以在 Theory category at forums.fast.ai. 探讨文章中的一些理论知识。
介绍
机器学习论文和实际软件操作过程比如 PyTorch 存在很大的差异。因为后者通过内置的自动微分功能隐藏了很多细节,如果想要了解最新的训练技术以及实现的底层,需要了解矩阵计算,这包括线性代数linear algebra和多元计算multivariate calculus。
例如,一个简单的神经网络计算单元首先计算权重向量 w \mathbb{w} w和输入向量 x \mathbb{x} x的点积,并加上一个标量(偏置)。公式为 z ( x ) = ∑ i n w i x i + b = w ⋅ x + b z(\mathbb{x})=\sum_{i}^nw_ix_i+b=\mathbb{w}\cdot\mathbb{x}+b z(x)=∑inwixi+b=w⋅x+b 通常该函数被称为为仿射函数(affine function)。然后紧接着一个线性整流单元rectified linear unit,它将负值裁剪为0: max ( 0 , z ( x ) ) \max(0, z(\mathbb{x})) max(0,z(x))。这个计算过程为定义为一个「人工神经元」。神经网络包含多个这样的单元。多个单元聚合成网络层,上一层的输出是下一层的输入。最后一层的输出称作神经网络的输出。
训练一个神神经网络意味着选择合适的权重向量 w \mathbb{w} w 和偏置 b b b,对于输入的所有向量 x \mathbb{x} x都会输出想要的结果。为此会设计一个损失函数,来对比所有输入网络推理的结果 a c t i v a t i o n ( x ) activation(\mathbb{x}) activation(x) 和预期结果 t a r g e t ( x ) target(\mathbb{x}) target(x) 的差异。为了最小化差异,通常使用SGD或者Adam等梯度下降方法训练。所有这些都需要 a c t i v a t i o n ( x ) activation(\mathbb{x}) activation(x)对于模型参数 w \mathbb{w} w和 b b b的偏导数。通过逐步调整 w \mathbb{w} w和 b b b使得总的损失函数值变得越来越小。
例如可以写一个标量版本的均方误差损失函数:
1 N ∑ x ( t a r g e t ( x ) − a c t i v a t i o n ( x ) ) 2 = 1 N ∑ x ( t a r g e t ( x ) − max ( 0 , ∑ 1 ∣ x ∣ w i x i + b ) ) 2 \frac{1}{N}\sum_{\mathbb{x}}\left(target(\mathbf{x}) - activation(\mathbb{x})\right)^2=\frac{1}{N}\sum_{\mathbb{x}}\left(target(\mathbb{x}) - \max(0, \sum_{1}^{|x|}w_ix_i+b)\right)^2 N1x∑(target(x)−activation(x))2=N1x∑⎝⎛target(x)−max(0,1∑∣x∣wixi+b)⎠⎞2
∣ x ∣ |x| ∣x∣表示向量 x x x中元素的个数, 注意这只是一个神经元,神经网络需要同时训练所有层的所有神经元。由于有多个输入和多个网络输出,通常需要一些向量对向量和求导法则。这篇文章的目的于此。
复习:标量求导法则
对于标量的求导法则如下:
| Rule | f ( x ) f(x) f(x) | 对 x x x 导数 | 例子 |
|---|---|---|---|
| 常量 | c c c | 0 | d d x 99 = 0 \frac{d}{dx}99=0 dxd99=0 |
| 与常量乘 | c f cf cf | c d f d x c\frac{df}{dx} cdxdf | d d x 3 x = 3 \frac{d}{dx}3x=3 dxd3x=3 |
| 幂 | x n x^n xn | n x n − 1 nx^{n-1} nxn−1 | d d x x 3 = 3 x 2 \frac{d}{dx}x^3=3x^2 dxdx3=3x2 |
| 和 | f + g f+g f+g | d f d x + d g d x \frac{df}{dx}+\frac{dg}{dx} dxdf+dxdg | d d x ( x 2 + 3 x ) = 2 x + 3 \frac{d}{dx}(x^2+3x)=2x+3 dxd(x2+3x)=2x+3 |
| 积 | f g fg fg | f d g d x + g d f d x f\frac{dg}{dx}+g\frac{df}{dx} fdxdg+gdxdf | d d x x 2 x = x 2 + x 2 x = 3 x 2 \frac{d}{dx}x^2x=x^2+x2x=3x^2 dxdx2x=x2+x2x=3x2 |
| 链式法则 | f ( g ( x ) ) f(g(x)) f(g(x)) | d f ( u ) d u d u d x , u = g ( x ) \frac{df(u)}{du}\frac{du}{dx}, u= g(x) dudf(u)dxdu,u=g(x) | d d x ln ( x 2 ) = 1 x 2 2 x = 2 x \frac{d}{dx}\ln(x^2)=\frac{1}{x^2}2x=\frac{2}{x} dxdln(x2)=x212x=x2 |
向量计算和偏导数
神经网络层并不是由一个参数和一个方程构成的。首先考虑多个参数的情况,例如 f ( x , y ) = 3 x 2 y f(x,y) = 3x^2y f(x,y)=3x2y。此时, f ( x , y ) f(x, y) f(x,y) 的变化取决于更改 x x x 还是更改 y y y 。引出偏导(partial derivatives)。例如对于 x x x 偏导可以写为 ∂ ∂ x 3 y x 2 \frac{\partial}{\partial x}3yx^2 ∂x∂3yx2 将 y y y 看作常量,可以得到偏导结果为 ∂ ∂ x 3 y x 2 = 3 y ∂ ∂ x x 2 = 6 y x \frac{\partial}{\partial x}3yx^2=3y\frac{\partial}{\partial x}x^2=6yx ∂x∂3yx2=3y∂x∂x2=6yx
从整体来看,当考虑整个向量的计算而不是多元函数的计算。对于 f ( x , y ) f(x, y) f(x,y) 需要计算 ∂ ∂ x f ( x , y ) \frac{\partial}{\partial x}f(x, y) ∂x∂f(x,y) 和 ∂ ∂ y f ( x , y ) \frac{\partial}{\partial y}f(x, y) ∂y∂f(x,y) 。可以将他们组合成水平向量,因此定义 f ( x , y ) f(x, y) f(x,y) 的导数为:
∇ f ( x , y ) = [ ∂ f ( x , y ) ∂ x , ∂ f ( x , y ) ∂ y ] = [ 6 y x , 3 x 2 ] \nabla f(x, y) = \left[\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y}\right] = \left[6yx, 3x^2\right] ∇f(x,y)=[∂x∂f(x,y),∂y∂f(x,y)]=[6yx,3x2]
因此一个多元函数的导数为偏导构成的向量。 他们将 n n n 个标量参数映射到一个标量。下一节将讨论如何处理多个多元函数的导数。
矩阵计算
当从一个多元函数考虑到多个多元函数的导数时,需要从向量运算考虑到矩阵运算。现在考虑两个函数的偏导,例如 f ( x , y ) = 3 x 2 y f(x, y) = 3x^2y f(x,y)=3x2y 和 g ( x , y ) = 2 x + y 8 g(x, y) = 2x + y^8 g(x,y)=2x+y8 。可以分别计算他们的梯度向量并堆叠在一次。此时这个矩阵称为 Jacobian ( Jacobian matrix) ,如下
J = [ ∇ f ( x , y ) ∇ g ( x , y ) ] = [ ∂ f ( x , y ) ∂ x ∂ f ( x , y ) ∂ y ∂ g ( x , y ) ∂ x ∂ g ( x , y ) ∂ y ] = [ 6 y x 3 x 2 2 8 y 7 ] J =\begin{bmatrix}\nabla f(x, y)\\ \nabla g(x, y)\end{bmatrix} = \begin{bmatrix} \frac{\partial f(x, y)}{\partial x}&\frac{\partial f(x, y)}{\partial y}\\ \frac{\partial g(x, y)}{\partial x}&\frac{\partial g(x, y)}{\partial y} \end{bmatrix}= \begin{bmatrix} 6yx & 3x^2\\2&8y^7 \end{bmatrix} J=[∇f(x,y)∇g(x,y)]=[∂x∂f(x,y)∂x∂g(x,y)∂y∂f(x,y)∂y∂g(x,y)]=[6yx23x28y7]
这种形式为分子布局(numerator layout) 对应另外一种为分母布局(denominat layout), 是对上述矩阵的转置。
Jacobian 矩阵生成
第一步,将多个标量通过向量表示。 f ( x , y , z ) → f ( x ) f(x, y, z) \to f(\mathbb{x}) f(x,y,z)→f(x)。定义默认情况下向量为列向量 n × 1 n\times 1 n×1,即
x = [ x 1 x 2 ⋮ x n ] \mathbb{x}= \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} x=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤
当有多个结果是标量的函数组合起来,通过 y = f ( x ) \mathbb{y}=\mathbb{f(x)} y=f(x) 表示。其中 y \mathbb{y} y 是一个向量表示 m m m 个结果为标量的方程,每个方程输入元素个数为 n = ∣ x ∣ n=|\mathbb{x}| n=∣x∣ 的向量。展开如下:
y 1 = f 1 ( x ) y 2 = f 2 ( x ) ⋮ y m = f m ( x ) \begin{aligned} y_1 &= f_1(\mathbb{x})\\ y_2 &= f_2(\mathbb{x})\\ &\vdots\\ y_m &=f_m(\mathbb{x}) \end{aligned} y1y2ym=f1(x)=f2(x)⋮=fm(x)
例如上一节的公式可以用 x 1 , x 2 x_1,x_2 x1,x2分别表示 x , y x, y x,y:
y 1 = f 1 ( x ) = 3 x 1 2 x 2 y 2 = f 2 ( x ) = 2 x 1 + x 2 8 \begin{aligned} y_1 &= f_1(\mathbb{x}) =3x_1^2x_2\\ y_2 &= f_2(\mathbb{x}) = 2x_1 + x_2^8 \end{aligned} y1y2=f1(x)=3x12x2=f2(x)=2x1+x28
通常Jacobian矩阵包含所有 m × n m\times n m×n 个偏导。它记录了 m m m个结果是标量函数对于 x \mathbb{x} x 的梯度
∂ y ∂ x = [ ∇ f 1 ( x ) ∇ f 2 ( x ) ⋮ ∇ f m ( x ) ] = [ ∂ ∂ x f 1 ( x ) ∂ ∂ x f 2 ( x ) ⋮ ∂ ∂ x f m ( x ) ] = [ ∂ ∂ x 1 f 1 ( x ) ∂ ∂ x 2 f 1 ( x ) ⋯ ∂ ∂ x n f 1 ( x ) ∂ ∂ x 1 f 2 ( x ) ∂ ∂ x 2 f 2 ( x ) ⋯ ∂ ∂ x n f 2 ( x ) ⋮ ⋮ ⋮ ∂ ∂ x 1 f m ( x ) ∂ ∂ x 2 f m ( x ) ⋯ ∂ ∂ x n f m ( x ) ] \frac{\partial\mathbb{y}}{\partial\mathbb{x}}= \begin{bmatrix} \nabla f_1(\mathbb{x})\\ \nabla f_2(\mathbb{x})\\ \vdots \\ \nabla f_m(\mathbb{x}) \end{bmatrix}= \begin{bmatrix} \frac{\partial}{\partial\mathbb{x}}f_1(\mathbb{x})\\ \frac{\partial}{\partial\mathbb{x}}f_2(\mathbb{x})\\ \vdots\\ \frac{\partial}{\partial\mathbb{x}}f_m(\mathbb{x}) \end{bmatrix}= \begin{bmatrix} \frac{\partial}{\partial x_1}f_1(\mathbb{x}) & \frac{\partial}{\partial x_2}f_1(\mathbb{x}) &\cdots &\frac{\partial}{\partial x_n}f_1(\mathbb{x})\\ \frac{\partial}{\partial x_1}f_2(\mathbb{x}) & \frac{\partial}{\partial x_2}f_2(\mathbb{x}) &\cdots & \frac{\partial}{\partial x_n} f_2(\mathbb{x})\\ \vdots &\vdots&&\vdots\\ \frac{\partial}{\partial x_1}f_m(\mathbb{x}) &\frac{\partial}{\partial x_2}f_m(\mathbb{x}) &\cdots &\frac{\partial}{\partial x_n}f_m(\mathbb{x}) \end{bmatrix} ∂x∂y=⎣⎢⎢⎢⎡∇f1(x)∇f2(x)⋮∇fm(x)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡∂x∂f1(x)∂x∂f2(x)⋮∂x∂fm(x)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x)⎦⎥⎥⎥⎤
每个 ∂ ∂ x f i ( x ) \frac{\partial}{\partial \mathbb{x}}f_i(\mathbb{x}) ∂x∂fi(x) 是一个 n = ∣ x ∣ n=|\mathbb{x}| n=∣x∣ 元水平向量。
下面考虑恒等式 f ( x ) = x \mathbb{f(x) = x} f(x)=x, f i ( x ) = x f_i(\mathbf{x})=\mathbf{x} fi(x)=x ,该恒等式包含 n n n 个函数每个函数包含 n n n 个参数,那么其 Jacobian矩阵是一个方阵 m = n m=n m=n。
∂ b ∂ x = [ ∂ ∂ x f 1 ( x ) ∂ ∂ x f 2 ( x ) ⋮ ∂ ∂ x f m ( x ) ] = [ ∂ ∂ x 1 f 1 ( x ) ∂ ∂ x 2 f 1 ( x ) ⋯ ∂ ∂ x n f 1 ( x ) ∂ ∂ x 1 f 2 ( x ) ∂ ∂ x 2 f 2 ( x ) ⋯ ∂ ∂ x n f 2 ( x ) ⋮ ⋮ ⋮ ∂ ∂ x 1 f m ( x ) ∂ ∂ x 2 f m ( x ) ⋯ ∂ ∂ x n f m ( x ) ] = [ ∂ ∂ x 1 x 1 ∂ ∂ x 2 x 1 ⋯ ∂ ∂ x n x 1 ∂ ∂ x 1 x 2 ∂ ∂ x 2 x 2 ⋯ ∂ ∂ x n x 2 ⋮ ⋮ ⋮ ∂ ∂ x 1 x n ∂ ∂ x 2 x n ⋯ ∂ ∂ x n x n ] = I \begin{aligned} \frac{\partial\mathbf{b}}{\partial\mathbf{x}}= \begin{bmatrix} \frac{\partial}{\partial\mathbf{x}}f_1(\mathbf{x})\\ \frac{\partial}{\partial\mathbf{x}}f_2(\mathbf{x})\\ \vdots\\ \frac{\partial}{\partial\mathbf{x}}f_m(\mathbf{x}) \end{bmatrix} &= \begin{bmatrix} \frac{\partial}{\partial x_1}f_1(\mathbb{x}) & \frac{\partial}{\partial x_2}f_1(\mathbb{x}) &\cdots &\frac{\partial}{\partial x_n}f_1(\mathbb{x})\\ \frac{\partial}{\partial x_1}f_2(\mathbb{x}) & \frac{\partial}{\partial x_2}f_2(\mathbb{x}) &\cdots & \frac{\partial}{\partial x_n} f_2(\mathbb{x})\\ \vdots &\vdots&&\vdots\\ \frac{\partial}{\partial x_1}f_m(\mathbb{x}) &\frac{\partial}{\partial x_2}f_m(\mathbb{x}) &\cdots &\frac{\partial}{\partial x_n}f_m(\mathbb{x}) \end{bmatrix}\\ &= \begin{bmatrix} \frac{\partial}{\partial x_1}x_1 & \frac{\partial}{\partial x_2}x_1 &\cdots &\frac{\partial}{\partial x_n}x_1\\ \frac{\partial}{\partial x_1}x_2 & \frac{\partial}{\partial x_2}x_2 &\cdots & \frac{\partial}{\partial x_n} x_2 \\ \vdots &\vdots&&\vdots\\ \frac{\partial}{\partial x_1}x_n &\frac{\partial}{\partial x_2}x_n &\cdots &\frac{\partial}{\partial x_n}x_n \end{bmatrix}\\ &=I \end{aligned} ∂x∂b=⎣⎢⎢⎢⎡∂x∂f1(x)∂x∂f2(x)⋮∂x∂fm(x)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡∂x1∂x1∂x1∂x2⋮∂x1∂xn∂x2∂x1∂x2∂x2⋮∂x2∂xn⋯⋯⋯∂xn∂x1∂xn∂x2⋮∂xn∂xn⎦⎥⎥⎥⎤=I
向量元素级二元运算符的导数
很多向量复杂计算可以简化为多个元素级向量二元操作的组合。例如通过 y = f ( w ) ◯ g ( w ) \mathbf{y}=\mathbf{f(w)}\bigcirc\mathbf{g(w)} y=f(w)◯g(w)其中 m = n = ∣ y ∣ = ∣ w ∣ = ∣ x ∣ m = n=|\mathbb{y}|=|\mathbb{w}|=|\mathbb{x}| m=n=∣y∣=∣w∣=∣x∣,例如下面这个例子
[ y 1 y 2 ⋮ y n ] = [ f 1 ( w ) ◯ g 1 ( x ) f 2 ( w ) ◯ g 2 ( x ) ⋮ f n ( w ) ◯ g n ( x ) ] \begin{bmatrix} y_1\\ y2\\ \vdots\\y_n \end{bmatrix}= \begin{bmatrix} f_1(\mathbf{w})\bigcirc g_1(\mathbf{x})\\ f_2(\mathbf{w})\bigcirc g_2(\mathbf{x})\\ \vdots\\ f_n(\mathbf{w})\bigcirc g_n(\mathbf{x}) \end{bmatrix} ⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡f1(w)◯g1(x)f2(w)◯g2(x)⋮fn(w)◯gn(x)⎦⎥⎥⎥⎤
考虑对 x \mathbf{x} x的Jacobian
J w = ∂ y ∂ w = [ ∂ ∂ w 1 ( f 1 ( w ) ◯ g 1 ( x ) ) ∂ ∂ w 2 ( f 1 ( w ) ◯ g 1 ( x ) ) ⋯ ∂ ∂ w n ( f 1 ( w ) ◯ g 1 ( x ) ) ∂ ∂ w 1 ( f 2 ( w ) ◯ g 2 ( x ) ) ∂ ∂ w 2 ( f 2 ( w ) ◯ g 2 ( x ) ) ⋯ ∂ ∂ w n ( f 2 ( w ) ◯ g 2 ( x ) ) ⋮ ⋮ ⋮ ∂ ∂ w 1 ( f n ( w ) ◯ g n ( x ) ) ∂ ∂ w 2 ( f n ( w ) ◯ g n ( x ) ) ⋯ ∂ ∂ w n ( f n ( w ) ◯ g n ( x ) ) ] J_\mathbf{w}=\frac{\partial\mathbf{y}}{\partial\mathbf{w}}= \begin{bmatrix} \frac{\partial}{\partial w_1}\left(f_1(\mathbf{w})\bigcirc g_1(\mathbf{x})\right) &\frac{\partial}{\partial w_2}\left(f_1(\mathbf{w})\bigcirc g_1(\mathbf{x})\right) &\cdots &\frac{\partial}{\partial w_n}\left(f_1(\mathbf{w})\bigcirc g_1(\mathbf{x})\right)\\ \frac{\partial}{\partial w_1}\left(f_2(\mathbf{w})\bigcirc g_2(\mathbf{x})\right) &\frac{\partial}{\partial w_2}\left(f_2(\mathbf{w})\bigcirc g_2(\mathbf{x})\right) &\cdots &\frac{\partial}{\partial w_n}\left(f_2(\mathbf{w})\bigcirc g_2(\mathbf{x})\right)\\ \vdots & \vdots &&\vdots\\ \frac{\partial}{\partial w_1}\left(f_n(\mathbf{w})\bigcirc g_n(\mathbf{x})\right) &\frac{\partial}{\partial w_2}\left(f_n(\mathbf{w})\bigcirc g_n(\mathbf{x})\right) &\cdots &\frac{\partial}{\partial w_n}\left(f_n(\mathbf{w})\bigcirc g_n(\mathbf{x})\right)\\ \end{bmatrix} Jw=∂w∂y=⎣⎢⎢⎢⎡∂w1∂(f1(w)◯g1(x))∂w1∂(f2(w)◯g2(x))⋮∂w1∂(fn(w)◯gn(x))∂w2∂(f1(w)◯g1(x))∂w2∂(f2(w)◯g2(x))⋮∂w2∂(fn(w)◯gn(x))⋯⋯⋯∂wn∂(f1(w)◯g1(x))∂wn∂(f2(w)◯g2(x))⋮∂wn∂(fn(w)◯gn(x))⎦⎥⎥⎥⎤
上面的式子看起来比较麻烦,先考虑Jacobian是一个对角矩阵,即 ∂ ∂ w j ( f i ( w ) ◯ g i ( x ) ) = 0 , i ≠ j \frac{\partial}{\partial w_j}\left(f_i(\mathbf{w})\bigcirc g_i(\mathbf{x})\right) = 0, i\neq j ∂wj∂(fi(w)◯gi(x))=0,i=j 。此时非对角线上的元素恒为0。 f i f_i fi 只是一个和 w i w_i wi 有关的函数,此时二元表达式可以简化为 f i ( w i ) ◯ g i ( x i ) f_i(w_i)\bigcirc g_i(x_i) fi(wi)◯gi(xi), Jacobian可以表示为:
∂ y ∂ w = d i a g ( ∂ ∂ w 1 ( f 1 ( w 1 ) ◯ g 1 ( x 1 ) ) , ∂ ∂ w 2 ( f 2 ( w 2 ) ◯ g 2 ( x 2 ) ) , ⋯ , ∂ ∂ w n ( f n ( w n ) ◯ g n ( x n ) ) ) \frac{\partial \mathbf{y}}{\partial\mathbf{w}}=diag\left(\frac{\partial}{\partial w_1}(f_1(w_1)\bigcirc g_1(x_1)), \frac{\partial}{\partial w_2}(f_2(w_2)\bigcirc g_2(x_2)), \cdots, \frac{\partial}{\partial w_n}(f_n(w_n)\bigcirc g_n(x_n))\right) ∂w∂y=diag(∂w1∂(f1(w1)◯g1(x1)),∂w2∂(f2(w2)◯g2(x2)),⋯,∂wn∂(fn(wn)◯gn(xn)))
对应偏导运算可以总结如下
| Op | Partial with Respect to w \mathbf{w} w |
|---|---|
| + + + | ∂ ( w + x ) ∂ w = d i a g ( ⋯ ∂ ( w i + x i ) ∂ w i ⋯ ) = I \frac{\partial(\mathbf{w} + \mathbf{x})}{\partial\mathbf{w}}=diag(\cdots\frac{\partial(w_i + x_i)}{\partial w_i}\cdots)=I ∂w∂(w+x)=diag(⋯∂wi∂(wi+xi)⋯)=I |
| − - − | ∂ ( w + x ) ∂ w = d i a g ( ⋯ ∂ ( w i − x i ) ∂ w i ⋯ ) = I \frac{\partial(\mathbf{w} + \mathbf{x})}{\partial\mathbf{w}}=diag(\cdots\frac{\partial{(w_i - x_i)}}{\partial w_i}\cdots)=I ∂w∂(w+x)=diag(⋯∂wi∂(wi−xi)⋯)=I |
| ⊗ \otimes ⊗ | ∂ ( w ⊗ x ) ∂ w = d i a g ( ⋯ ∂ ( w i × x i ) ∂ w i ⋯ ) = d i a g ( x ) \frac{\partial(\mathbf{w}\otimes\mathbf{x})}{\partial\mathbf{w}}=diag\left(\cdots\frac{\partial(w_i\times x_i)}{\partial w_i}\cdots\right)=diag(\mathbf{x}) ∂w∂(w⊗x)=diag(⋯∂wi∂(wi×xi)⋯)=diag(x) |
| ⊘ \oslash ⊘ | ∂ ( w ⊘ x ) ∂ w = d i a g ( ⋯ ∂ ( w i / x i ) ∂ w i ⋯ ) = d i a g ( ⋯ 1 x i ⋯ ) \frac{\partial(\mathbf{w}\oslash\mathbf{x})}{\partial\mathbf{w}}=diag\left(\cdots\frac{\partial(w_i/ x_i)}{\partial w_i}\cdots\right)=diag(\cdots\frac{1}{x_i}\cdots) ∂w∂(w⊘x)=diag(⋯∂wi∂(wi/xi)⋯)=diag(⋯xi1⋯) |
对 x \mathbf{x} x 的偏导
| OP | Partial With Respect to x \mathbf{x} x |
|---|---|
| + + + | ∂ ( w + x ) ∂ x = I \frac{\partial(\mathbf{w+x})}{\partial\mathbf{x}}=I ∂x∂(w+x)=I |
| − - − | ∂ ( w − x ) ∂ x = − I \frac{\partial(\mathbf{w-x})}{\partial\mathbf{x}}=-I ∂x∂(w−x)=−I |
| ⊗ \otimes ⊗ | ∂ ( w ⊗ x ) ∂ x = d i a g ( w ) \frac{\partial(\mathbf{w\otimes x})}{\partial\mathbf{x}}=diag(\mathbf{w}) ∂x∂(w⊗x)=diag(w) |
| ⊘ \oslash ⊘ | ∂ ( w ⊘ x ) ∂ x = d i a g ( ⋯ − w i x i 2 ⋯ ) \frac{\partial(\mathbf{w\oslash x})}{\partial\mathbf{x}}=diag\left(\cdots\frac{-w_i}{x_i^2}\cdots\right) ∂x∂(w⊘x)=diag(⋯xi2−wi⋯) |
其中 ⊗ \otimes ⊗ 和 ⊘ \oslash ⊘ 表示元素间乘除法。
涉及标量运算的导数
当使用标量和向量之间的运算,例如乘法或者加法时,可以把标量拓展为向量并表示为两个向量之前二元运算。例如,将标量 z z z 与向量 x \mathbf{x} x 相加 y = x + z = f ( x ) + g ( z ) \mathbf{y} = \mathbf{x} + z=f(\mathbf{x}) + g(z) y=x+z=f(x)+g(z) 此时 f ( x ) = x f(\mathbf{x})=\mathbf{x} f(x)=x , g ( z ) = 1 ⃗ z g(z) = \vec{1}z g(z)=1z 。同理 y = x z = x ⊗ 1 ⃗ z \mathbf{y}=\mathbf{x}z=\mathbf{x}\otimes\vec{1}z y=xz=x⊗1z 。 此时可以通过上一节的内容来计算导数。
∂ y ∂ x = d i a g ( ⋯ ∂ ∂ ( f i ( x i ) ◯ g i ( z ) ) ⋯ ) \frac{\partial\mathbf{y}}{\partial\mathbf{x}}=diag\left(\cdots \frac{\partial}{\partial}(f_i(x_i)\bigcirc g_i(z))\cdots\right) ∂x∂y=diag(⋯∂∂(fi(xi)◯gi(z))⋯)
对应可得
∂ ∂ x ( x + z ) = d i a g ( 1 ⃗ ) = I ∂ ∂ z ( x + z ) = d i a g ( 1 ⃗ ) = I \frac{\partial}{\partial\mathbf{x}}(\mathbf{x} + z) = diag(\vec{1})= I\\ \frac{\partial}{\partial z}(\mathbf{x} + z) = diag(\vec{1})= I ∂x∂(x+z)=diag(1)=I∂z∂(x+z)=diag(1)=I
∂ ∂ x ( x z ) = d i a g ( 1 ⃗ z ) = I z ∂ ∂ z ( x z ) = x \frac{\partial}{\partial\mathbf{x}}(\mathbf{x}z)=diag(\vec{1}z) = Iz\\ \frac{\partial}{\partial z}(\mathbf{x}z)= \mathbf{x} ∂x∂(xz)=diag(1z)=Iz∂z∂(xz)=x
关于最后一个等式推导如下, x x x 是一个列向量:
∂ ∂ z ( f i ( x i ) ⊗ g i ( z ) ) = x i ∂ z ∂ z + z ∂ x i ∂ z = x i + 0 = x i \frac{\partial}{\partial z}(f_i(x_i)\otimes g_i(z) ) = x_i\frac{\partial z}{\partial z} + z\frac{\partial x_i}{\partial z} = x_i + 0 = x_i ∂z∂(fi(xi)⊗gi(z))=xi∂z∂z+z∂z∂xi=xi+0=xi
向量对向量求导:结果是矩阵
向量对标量求导:结果是向量
向量归约和(sum reduction)
深度学习通常会计算向量中所有元素的和,例如网络的损失函数。可以通过向量点乘或者其他操作把向量转化为标量。
令 y = ∑ ( f ( x ) ) = ∑ i = 1 n f i ( x ) y=\sum(\mathbf{f(x)}) = \sum_{i=1}^nf_i(\mathbf{x}) y=∑(f(x))=∑i=1nfi(x) ,注意每个函数的参数都是向量 x \mathbf{x} x 。对应雅可比矩阵为 1 × n 1\times n 1×n 向量:
∂
y
∂
x
=
[
∂
y
∂
x
1
,
∂
y
∂
x
2
,
⋯
,
∂
y
∂
x
n
]
=
[
∂
∂
x
1
∑
i
f
i
(
x
)
,
∂
∂
x
2
∑
i
f
i
(
x
)
,
⋯
,
∂
∂
x
n
∑
i
f
i
(
x
)
]
=
[
∑
i
∂
f
i
(
x
)
∂
x
1
,
∑
i
∂
f
i
(
x
)
∂
x
2
,
⋯
,
∑
i
∂
f
i
(
x
)
∂
x
n
]
(
move derivate inside
∑
)
\begin{aligned} \frac{\partial y}{\partial\mathbf{x}}&= \begin{bmatrix} \frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2}, \cdots,\frac{\partial y}{\partial x_n} \end{bmatrix}\\ &= \begin{bmatrix} \frac{\partial}{\partial x_1}\sum_i f_i(\mathbf{x}), \frac{\partial}{\partial x_2}\sum_if_i(\mathbf{x}),\cdots,\frac{\partial}{\partial x_n}\sum_if_i(\mathbf{x}) \end{bmatrix}\\ &= \begin{bmatrix} \sum_i\frac{\partial f_i(\mathbf{x})}{\partial x_1}, \sum_i\frac{\partial f_i(\mathbf{x})}{\partial x_2},\cdots,\sum_i\frac{\partial f_i(\mathbf{x})}{\partial x_n} \end{bmatrix} (\text{move derivate inside} \sum) \end{aligned}
∂x∂y=[∂x1∂y,∂x2∂y,⋯,∂xn∂y]=[∂x1∂∑ifi(x),∂x2∂∑ifi(x),⋯,∂xn∂∑ifi(x)]=[∑i∂x1∂fi(x),∑i∂x2∂fi(x),⋯,∑i∂xn∂fi(x)](move derivate inside∑)
考虑最简单的情况
y
=
s
u
m
(
x
)
y = sum(\mathbf{x})
y=sum(x) , 此时
f
i
(
x
)
=
x
i
f_i(\mathbf{x})=x_i
fi(x)=xi
∇
y
=
[
∑
i
∂
x
i
∂
x
1
,
∑
i
∂
x
i
∂
x
2
,
⋯
,
∑
i
∂
x
i
∂
x
n
]
=
[
1
,
1
,
⋯
,
1
]
=
1
⃗
T
\nabla y = \begin{bmatrix} \sum_i\frac{\partial x_i}{\partial x_1},\sum_i\frac{\partial x_i}{\partial x_2},\cdots,\sum_i\frac{\partial x_i}{\partial x_n} \end{bmatrix} = [1, 1,\cdots,1] = \vec{1}^T
∇y=[∑i∂x1∂xi,∑i∂x2∂xi,⋯,∑i∂xn∂xi]=[1,1,⋯,1]=1T
此时结果是一个全1的行向量。
考虑另外一种情况: y = s u m ( x z ) y= sum(\mathbf{x}z) y=sum(xz) , f i ( x , z ) = x i z f_i(\mathbf{x}, z)=x_iz fi(x,z)=xiz, 梯度为
∂ y ∂ x = [ ∑ i ∂ ∂ x 1 x i z , ∑ i ∂ ∂ x 2 x i z , ⋯ , ∑ i ∂ ∂ x n x i z ] = [ z , z , ⋯ , z ] \begin{aligned} \frac{\partial y}{\partial \mathbf{x}} &= \begin{bmatrix} \sum_i\frac{\partial}{\partial x_1}x_iz,\sum_i\frac{\partial}{\partial x_2}x_iz, \cdots, \sum_i\frac{\partial}{\partial x_n}x_iz \end{bmatrix}\\ &= \begin{bmatrix} z, z,\cdots, z \end{bmatrix} \end{aligned} ∂x∂y=[∑i∂x1∂xiz,∑i∂x2∂xiz,⋯,∑i∂xn∂xiz]=[z,z,⋯,z]
现在考虑对于标量 z z z 的梯度,其结果是 1 × 1 1\times 1 1×1标量
∂ y ∂ z = ∂ ∂ z ∑ i = 1 n x i z = ∑ i ∂ ∂ z x i z = ∑ i x i = s u m ( x ) \begin{aligned} \frac{\partial\mathbf{y}}{\partial z} &= \frac{\partial}{\partial z}\sum_{i=1}^n x_iz\\ &= \sum_i\frac{\partial}{\partial z}x_i z\\ &= \sum_ix_i\\ &=sum(\mathbf{x}) \end{aligned} ∂z∂y=∂z∂i=1∑nxiz=i∑∂z∂xiz=i∑xi=sum(x)
链式法则
从上面可以知道,复杂的函数计算可以通过基本的矩阵运算来实现。例如通常不能够直接计算嵌套表达式的梯度如 s u m ( w + x ) sum(\mathbf{w + x}) sum(w+x) (除非将它门展开为标量计算)。 但是可以通过链式法则组合基本的矩阵求导法则来计算。下面先举例解释单变量链式法则(single-variable chain rule)。即标量方程对标量求导。进而推广到全导数(total derivative)并且使用它去定义单变量全导数链式法则(single-variable total-derivative chain rule)。它在神经网络中受到广泛的应用。
Single-variable chain rule
链式法则也是一种分而治之的策略。将复杂的表达式分解为子表达式,且子表达式的导数更方便求解。例如求解 d d x s i n ( x 2 ) = 2 x c o s ( x 2 ) \frac{d}{dx}sin(x^2)=2xcos(x^2) dxdsin(x2)=2xcos(x2) 外层的 s i n sin sin 可以使用内层表达式的结果。 d d x x 2 = 2 x \frac{d}{dx}x^2 = 2x dxdx2=2x , d d u s i n ( u ) = c o s ( u ) \frac{d}{du}sin(u)=cos(u) dudsin(u)=cos(u) 。看起来像是外部函数的导数和内部函数的导数链接起来。通常复合函数可以被写作 y = f ( g ( x ) ) y=f(g(x)) y=f(g(x)) 或者 ( f ∘ g ) ( x ) (f\circ g)(x) (f∘g)(x) 。 y = f ( u ) , u = g ( x ) y = f(u), u= g(x) y=f(u),u=g(x) 链式法则可以表示为
d y d x = d y d u d u d x \frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx} dxdy=dudydxdu
- 通过中间变量把复杂函数求导转化为两个简单函数的求导
- 分别计算两个简单函数的导数
- 两个导数结果想乘
- 替换中间变量
链式法则也可以通过数据流或者抽象语法树(abstract syntax tree)表示

如上图所示,更改参数 x x x 会通过平方和正弦函数作用于 y y y 。可以把 d u d x \frac{du}{dx} dxdu 理解为 x x x 的变化传导到 u u u。 链式法则可以表示为 d y d x = d u d x d y d u \frac{dy}{dx}=\frac{du}{dx}\frac{dy}{du} dxdy=dxdududy (x到y)
Single-variable chain rule 应用场景:注意上图 x x x 到 y y y 只有一条数据流。因此 x x x 的改变仅能通过一条路径影响到 y y y 。 但是如果表达式为 y ( x ) = x + x 2 y(x) = x + x^2 y(x)=x+x2 ,它表达为 y ( x , u ) = x + u , 此 时 y(x, u) = x + u,此时 y(x,u)=x+u,此时 y ( x , u ) y(x, u) y(x,u) 的数据流图有多条路径,此时应该使用单变量全微分链式法则(single-variable total-derivative chain rule)。可以先考虑下面这个式子 y = f ( x ) = l n ( s i n ( x 3 ) 2 ) y = f(x)=ln(sin(x^3)^2) y=f(x)=ln(sin(x3)2), 过程如下:
-
使用中间变量
u 1 = f 1 ( x ) = x 3 u 2 = f 2 ( u 1 ) = s i n ( u 1 ) u 3 = f 3 ( u 2 ) = u 2 2 u 4 = f 4 ( u 3 ) = l n ( u 3 ) ( y = u 4 ) \begin{aligned} u_1 &= f_1(x) = x^3\\ u_2 &= f_2(u_1)= sin(u_1)\\ u_3 &= f_3(u_2) = u_2^2\\ u_4 &= f_4(u_3) =ln(u_3)(y = u_4) \end{aligned} u1u2u3u4=f1(x)=x3=f2(u1)=sin(u1)=f3(u2)=u22=f4(u3)=ln(u3)(y=u4) -
计算微分
d d u x u 1 = 3 x 2 d d u 1 u 2 = c o s ( u 1 ) d d u 2 u 3 = 2 u 2 d d u 3 u 5 = 1 u 3 \begin{aligned} \frac{d}{du_x}u_1 &= 3 x^2\\ \frac{d}{du_1}u_2&= cos(u_1)\\ \frac{d}{du_2}u_3 &= 2u_2\\ \frac{d}{du_3}u_5 &= \frac{1}{u_3} \end{aligned} duxdu1du1du2du2du3du3du5=3x2=cos(u1)=2u2=u31 -
组合四个中间变量
d y d x = d u 4 d x = 1 u 3 2 u 2 c o s ( u 1 ) 3 x 2 = 6 u 2 x 2 c o s ( u 1 ) u 3 \frac{dy}{dx} = \frac{du_4}{dx} = \frac{1}{u_3}2u_2cos(u_1)3x^2 = \frac{6u_2x^2cos(u_1)}{u_3} dxdy=dxdu4=u312u2cos(u1)3x2=u36u2x2cos(u1) -
替换中间变量
d y d x = 6 s i n ( u 1 ) x 2 c o s ( x 3 ) u 2 2 = 6 s i n ( x 3 ) x 2 c o s ( x 3 ) s i n ( x 3 ) 2 = 6 x 2 c o s ( x 3 ) s i n ( x 3 ) \frac{dy}{dx} = \frac{6sin(u_1)x^2cos(x^3)}{u_2^2} = \frac{6sin(x^3)x^2cos(x^3)}{sin(x^3)^2} = \frac{6x^2cos(x^3)}{sin(x^3)} dxdy=u226sin(u1)x2cos(x3)=sin(x3)26sin(x3)x2cos(x3)=sin(x3)6x2cos(x3)
可视化链式法则如下图(1条路径)

Single-variable total-derivative chain rule
单变量链式法则应用范围有限,因为每个中心变量都必须是单变量的函数。但是它展示了链式法则的核心。如果想要对 y = f ( x ) = x + x 2 y=f(x)=x + x^2 y=f(x)=x+x2 通过链式法则求导,需要对基本的链式法则做增强。
显然可以直接求导 d y d x = d d x x + d d x x 2 = 1 + 2 x \frac{dy}{dx}=\frac{d}{dx}x + \frac{d}{dx}x^2 = 1 + 2x dxdy=dxdx+dxdx2=1+2x。但是它应用了变量加法的导数法则而不是链式法则。先尝试用链式法则来计算
u 1 ( x ) = x 2 u 2 ( x , u 1 ) = x + u 1 ( y = f ( x ) = u 2 ( x , u 1 ) ) \begin{aligned} u_1(x) &= x^2\\ u_2(x, u_1) &=x + u _1\quad(y=f(x)=u_2(x, u_1)) \end{aligned} u1(x)u2(x,u1)=x2=x+u1(y=f(x)=u2(x,u1))
先假设 d u 2 d u 1 = 0 + 1 = 1 \frac{du_2}{du_1} = 0 + 1 = 1 du1du2=0+1=1 和 d u 1 d x = 2 x \frac{du_1}{dx}=2x dxdu1=2x , 则 d y d x = d u 2 d x = d u 2 d u 1 d u 1 d x = 2 x \frac{dy}{dx} = \frac{du_2}{dx}=\frac{du_2}{du_1}\frac{du_1}{dx} = 2x dxdy=dxdu2=du1du2dxdu1=2x y与正确结果不相同。原因在于 u 2 ( x , u ) = x + u 1 u_2(x, u) = x + u_1 u2(x,u)=x+u1 有多个参数,此时需要引入偏导数。先尝试一下:
∂ u 1 ( x ) ∂ x = 2 x ∂ u 2 ( x , u 1 ) ∂ u 1 = ∂ ∂ u 1 ( x + u 1 ) = 0 + 1 = 1 ∂ u 2 ( x , u 1 ) ∂ x ≠ ∂ ∂ x ( x + u 1 ) = 1 + 0 = 1 \begin{aligned} \frac{\partial u_1(x)}{\partial x} &= 2x\\ \frac{\partial u_2(x,u_1)}{\partial u_1} &= \frac{\partial}{\partial u_1}(x + u_1) = 0 + 1= 1\\ \frac{\partial u_2(x, u_1)}{\partial x}&\neq \frac{\partial}{\partial x}(x + u_1) = 1 + 0 = 1 \end{aligned} ∂x∂u1(x)∂u1∂u2(x,u1)∂x∂u2(x,u1)=2x=∂u1∂(x+u1)=0+1=1=∂x∂(x+u1)=1+0=1
∂ u 2 ( x , u 1 ) ∂ x \frac{\partial u_2(x, u_1)}{\partial x} ∂x∂u2(x,u1) 出现问题,因为 u 1 u_1 u1 包含变量了 x x x。在计算偏导的时候不能把 u 1 u_1 u1 看作标量。可以通过如下计算图展示。
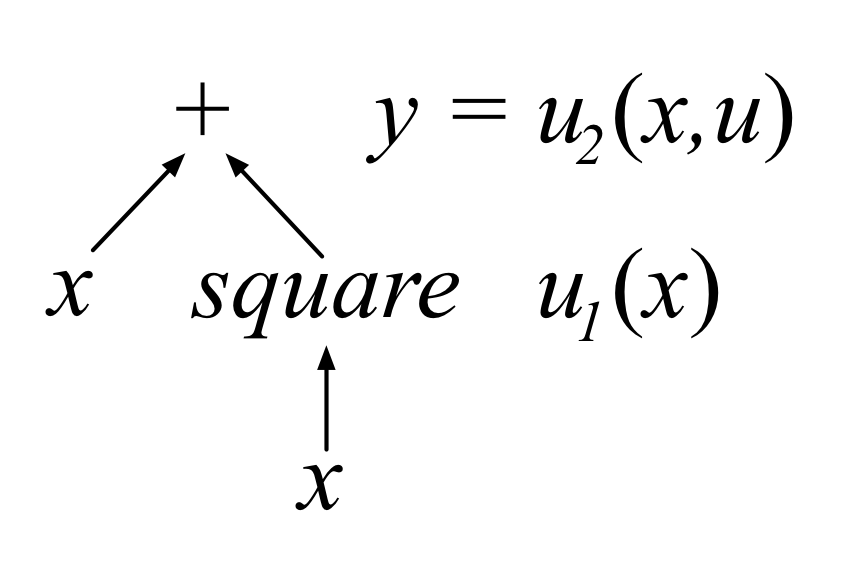
x x x 的变化会通过加法和平方运算影响到 y y y。下面的式子可以看出来 x x x 如何影响 y y y
y ^ = ( x + Δ x ) + ( x + Δ x ) 2 \hat{y} = (x +\Delta x) + (x +\Delta x)^2 y^=(x+Δx)+(x+Δx)2
Δ y = y ^ − y \Delta y = \hat{y} - y Δy=y^−y, 此时需要引出总导数( total derivatives), 他假设所有的中间变量都包含 x x x 并且可能随着 x x x 的变化而变化。公式如下:
d y d x = ∂ f ( x ) x = ∂ u 2 ( x , u 1 ) ∂ x = ∂ u 2 ∂ x ∂ x ∂ x + ∂ u 2 ∂ u 1 ∂ u 1 ∂ x = ∂ u 2 ∂ x + ∂ u 2 ∂ u 1 ∂ u 1 ∂ x \frac{dy}{dx}=\frac{\partial f(x)}{x} = \frac{\partial u_2(x, u_1)}{\partial x} = \frac{\partial u_2}{\partial x}\frac{\partial x}{\partial x} + \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} = \frac{\partial u_2}{\partial x} + \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} dxdy=x∂f(x)=∂x∂u2(x,u1)=∂x∂u2∂x∂x+∂u1∂u2∂x∂u1=∂x∂u2+∂u1∂u2∂x∂u1
带入公式:
d
y
d
x
=
∂
u
2
∂
x
+
∂
u
2
∂
u
1
∂
u
1
∂
x
=
1
+
1
×
2
x
=
1
=
2
x
\frac{dy}{dx} = \frac{\partial u_2}{\partial x} + \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} = 1 + 1\times2x = 1 = 2x
dxdy=∂x∂u2+∂u1∂u2∂x∂u1=1+1×2x=1=2x
单变量总导数链式法则(single-variable total-derivative chaine rule)总结如下:
∂
f
(
x
,
u
1
,
⋯
,
u
n
)
∂
x
=
∂
f
∂
x
+
∑
i
n
∂
f
∂
u
i
∂
u
i
∂
x
\frac{\partial f(x, u_1,\cdots,u_n)}{\partial x}=\frac{\partial f}{\partial x} + \sum_i^n\frac{\partial f}{\partial u_i}\frac{\partial u_i}{\partial x}
∂x∂f(x,u1,⋯,un)=∂x∂f+i∑n∂ui∂f∂x∂ui
下面例子
f
(
x
)
=
s
i
n
(
x
+
x
2
)
f(x) = sin(x + x^2)
f(x)=sin(x+x2)
u 1 ( x ) = x 2 u 2 ( x , u 1 ) = x + u 1 u 3 ( u 2 ) = s i n ( u 2 ) \begin{aligned} u_1(x) &= x^2\\ u_2(x, u_1) &= x + u_1\\ u_3(u_2) &= sin(u_2) \end{aligned} u1(x)u2(x,u1)u3(u2)=x2=x+u1=sin(u2)
对应偏导
∂ u 1 ∂ x = 2 x ∂ u 2 ∂ x = ∂ x ∂ x + ∂ u 2 ∂ u 1 ∂ u 1 ∂ x = 1 + 2 x ∂ f ( x ) ∂ x = ∂ u 3 ∂ x + ∂ u 3 ∂ u 2 ∂ u 2 ∂ x = 0 + c o s ( u 2 ) ∂ u 2 ∂ x = c o s ( x + x 2 ) ( 1 + 2 x ) \begin{aligned} \frac{\partial u_1}{\partial x} &= 2x\\ \frac{\partial u_2}{\partial x} &=\frac{\partial x}{\partial x} + \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}= 1 + 2x\\ \frac{\partial f(x)}{\partial x} &= \frac{\partial u_3}{\partial x} +\frac{\partial u_3}{\partial u_2}\frac{\partial u_2}{\partial x} = 0 + cos(u_2)\frac{\partial u_2}{\partial x} = cos(x + x^2)(1+2x) \end{aligned} ∂x∂u1∂x∂u2∂x∂f(x)=2x=∂x∂x+∂u1∂u2∂x∂u1=1+2x=∂x∂u3+∂u2∂u3∂x∂u2=0+cos(u2)∂x∂u2=cos(x+x2)(1+2x)
可以针对 f ( x ) = x 3 f(x) = x^3 f(x)=x3 应用法则:
u 1 ( x ) = x 2 u 2 ( x , u 1 ) = x u 1 ∂ u 1 ∂ x = 2 x ∂ u 2 ∂ x = u 1 + ∂ u 2 ∂ u 1 ∂ u 1 ∂ x = x 2 + x × 2 x = 3 x 2 \begin{aligned} u_1(x) &= x^2\\ u_2(x, u1) &= xu_1\\ \frac{\partial u_1}{\partial x} &= 2x\\ \frac{\partial u_2}{\partial x} &= u_1 + \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} = x^2 + x\times 2x = 3x^2 \end{aligned} u1(x)u2(x,u1)∂x∂u1∂x∂u2=x2=xu1=2x=u1+∂u1∂u2∂x∂u1=x2+x×2x=3x2
使用更多的中间变量,可以把求导分解成更简单的子问题。可以引入 x : u n + 1 = x x:u_{n+1} = x x:un+1=x 来更为清晰的展示链式法则:
∂ f ( u 1 , ⋯ , u n + 1 ) ∂ x = ∑ i = 1 n + 1 ∂ f ∂ u i ∂ u i ∂ x \frac{\partial f(u_1,\cdots, u_{n + 1})}{\partial x} = \sum_{i=1}^{n + 1}\frac{\partial f}{\partial u_i}\frac{\partial u_i}{\partial x} ∂x∂f(u1,⋯,un+1)=i=1∑n+1∂ui∂f∂x∂ui
向量链式法则
把标量表达式拓展到向量
y
=
f
(
x
)
\mathbf{y} = \mathbf{f}(x)
y=f(x), 例如
[
y
1
(
x
)
y
2
(
x
)
]
=
[
f
1
(
x
)
f
2
(
x
)
]
=
[
l
n
(
x
2
)
s
i
n
(
3
x
)
]
\begin{bmatrix} y_1(x)\\ y_2(x)\\ \end{bmatrix}= \begin{bmatrix} f_1(x)\\ f_2(x) \end{bmatrix}= \begin{bmatrix} ln(x^2)\\ sin(3x) \end{bmatrix}
[y1(x)y2(x)]=[f1(x)f2(x)]=[ln(x2)sin(3x)]
首先引入两个中间变量
g
1
g_1
g1 和
g
2
g_2
g2
[
g
1
(
x
)
g
2
(
x
)
]
=
[
x
2
3
x
]
[
f
1
(
g
)
f
2
(
g
)
]
=
[
l
n
(
g
1
)
s
i
n
(
g
2
)
]
\begin{aligned} \begin{bmatrix} g_1(x)\\ g_2(x) \end{bmatrix} &= \begin{bmatrix} x^2\\ 3x \end{bmatrix}\\ \begin{bmatrix} f_1(\mathbf{g})\\ f_2(\mathbf{g}) \end{bmatrix} &= \begin{bmatrix} ln(g_1)\\ sin(g_2) \end{bmatrix} \end{aligned}
[g1(x)g2(x)][f1(g)f2(g)]=[x23x]=[ln(g1)sin(g2)]
则关于标量
x
x
x 的导数构成的向量
y
\mathbf{y}
y 是一个列向量,可以通过单变量总导数链式法则计算
∂ y ∂ x = [ ∂ f 1 ( g ) ∂ x ∂ f 2 ( g ) ∂ x ] = [ ∂ f 1 ∂ g 1 ∂ g 1 ∂ x + ∂ f 1 ∂ g 2 ∂ g 2 ∂ x ∂ f 2 ∂ g 1 ∂ g 1 ∂ x + ∂ f 2 ∂ g 2 ∂ g 2 ∂ x ] = [ 1 g 1 2 x + 0 0 + c o s ( g 2 ) 3 ] = [ 2 x 3 c o s ( 3 x ) ] \frac{\partial\mathbf{y}}{\partial x} = \begin{bmatrix} \frac{\partial f_1(\mathbf{g})}{\partial x}\\ \frac{\partial f_2(\mathbf{g})}{\partial x} \end{bmatrix}= \begin{bmatrix} \frac{\partial f_1}{\partial g_1}\frac{\partial g_1}{\partial x} + \frac{\partial f_1}{\partial g_2}\frac{\partial g_2}{\partial x}\\ \frac{\partial f_2}{\partial g_1}\frac{\partial g_1}{\partial x} + \frac{\partial f_2}{\partial g_2}\frac{\partial g_2}{\partial x} \end{bmatrix} = \begin{bmatrix} \frac{1}{g_1}2x+0\\ 0 + cos(g_2)3 \end{bmatrix}= \begin{bmatrix} \frac{2}{x}\\ 3cos(3x) \end{bmatrix} ∂x∂y=[∂x∂f1(g)∂x∂f2(g)]=[∂g1∂f1∂x∂g1+∂g2∂f1∂x∂g2∂g1∂f2∂x∂g1+∂g2∂f2∂x∂g2]=[g112x+00+cos(g2)3]=[x23cos(3x)]
上个公式表明,可以通过标量的链式法则求导后将其组合为向量,更一般的,可以从下面表达式发现规律
∂ ∂ x f ( g ( x ) ) = [ ∂ f 1 ∂ g 1 ∂ g 1 ∂ x + ∂ f 1 ∂ g 2 ∂ g 2 ∂ x ∂ f 2 ∂ g 1 ∂ g 1 ∂ x + ∂ f 2 ∂ g 2 ∂ g 2 ∂ x ] = [ ∂ f 1 ∂ g 1 ∂ f 1 ∂ g 2 ∂ f 1 ∂ g 1 ∂ f 2 ∂ g 2 ] [ ∂ g 1 ∂ x ∂ g 2 ∂ x ] = ∂ f ∂ g ∂ g ∂ x \frac{\partial}{\partial x}\mathbf{f}(g(x))= \begin{bmatrix} \frac{\partial f_1}{\partial g_1}\frac{\partial g_1}{\partial x} + \frac{\partial f_1}{\partial g_2}\frac{\partial g_2}{\partial x}\\ \frac{\partial f_2}{\partial g_1}\frac{\partial g_1}{\partial x} + \frac{\partial f_2}{\partial g_2}\frac{\partial g_2}{\partial x} \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1}{\partial g_1} & \frac{\partial f_1}{\partial g_2}\\ \frac{\partial f_1}{\partial g_1} & \frac{\partial f_2}{\partial g_2} \end{bmatrix} \begin{bmatrix} \frac{\partial g_1}{\partial x}\\ \frac{\partial g_2}{\partial x} \end{bmatrix}= \frac{\partial \mathbf{f}}{\partial \mathbf{g}} \frac{\partial \mathbf{g}}{\partial x} ∂x∂f(g(x))=[∂g1∂f1∂x∂g1+∂g2∂f1∂x∂g2∂g1∂f2∂x∂g1+∂g2∂f2∂x∂g2]=[∂g1∂f1∂g1∂f1∂g2∂f1∂g2∂f2][∂x∂g1∂x∂g2]=∂g∂f∂x∂g
这说明Jacobian可以通过两个Jacobian乘法运算得到。更一般的,当输入是向量时,只需要把第二个向量用矩阵表示,如下表达式
∂
∂
x
f
(
g
(
x
)
)
=
∂
f
∂
g
∂
g
∂
x
=
[
f
1
g
1
f
1
g
2
⋯
f
1
g
k
f
2
g
1
f
2
g
2
⋯
f
2
g
k
⋮
⋮
⋮
f
m
g
1
f
m
g
2
⋯
f
m
g
k
]
[
∂
g
1
∂
x
1
∂
g
1
∂
x
2
⋯
∂
g
1
∂
x
n
∂
g
2
∂
x
1
∂
g
2
∂
x
1
⋯
∂
g
2
∂
x
n
⋮
⋮
⋮
∂
g
k
∂
x
1
∂
g
k
∂
x
2
⋯
∂
g
k
∂
x
n
]
\frac{\partial}{\partial \mathbf{x}}\mathbf{f(g(x))} = \frac{\partial \mathbf{f}}{\partial \mathbf{g}}\frac{\partial \mathbf{g}}{\partial\mathbf{x}} = \begin{bmatrix} \frac{f_1}{g_1} &\frac{f_1}{g_2} &\cdots &\frac{f_1}{g_k}\\ \frac{f_2}{g_1} &\frac{f_2}{g_2} &\cdots &\frac{f_2}{g_k}\\ \vdots &\vdots &&\vdots\\ \frac{f_m}{g_1}&\frac{f_m}{g_2} &\cdots&\frac{f_m}{g_k} \end{bmatrix} \begin{bmatrix} \frac{\partial g_1}{\partial x_1} &\frac{\partial g_1}{\partial x_2}&\cdots&\frac{\partial g_1}{\partial x_n}\\ \frac{\partial g_2}{\partial x_1} &\frac{\partial g_2}{\partial x_1}&\cdots&\frac{\partial g_2}{\partial x_n}\\ \vdots&\vdots&&\vdots\\ \frac{\partial g_k}{\partial x_1}& \frac{\partial g_k}{\partial x_2} &\cdots &\frac{\partial g_k}{\partial x_n} \end{bmatrix}
∂x∂f(g(x))=∂g∂f∂x∂g=⎣⎢⎢⎢⎢⎡g1f1g1f2⋮g1fmg2f1g2f2⋮g2fm⋯⋯⋯gkf1gkf2⋮gkfm⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡∂x1∂g1∂x1∂g2⋮∂x1∂gk∂x2∂g1∂x1∂g2⋮∂x2∂gk⋯⋯⋯∂xn∂g1∂xn∂g2⋮∂xn∂gk⎦⎥⎥⎥⎥⎤
从单变量链式拓展到向量形式一个直观的好处是,可以通过同样的公式表示总导数。上面的式子中 $m = |\mathbf{f}|, n = |\mathbf{x}|, k = |\mathbf{g}| $ 最终Jacobian为 m × n m\times n m×n 矩阵。
即使得到了 ∂ f ∂ g ∂ g ∂ x \frac{\partial \mathbf{f}}{\partial \mathbf{g}}\frac{\partial \mathbf{g}}{\partial \mathbf{x}} ∂g∂f∂x∂g 公式,很多情况下还可以做进一步简化。Jacobian 通常是方阵,并且非对角线元素是 0 。神经网络一般处理关于向量的方程,而不是方程构成的向量。例如,对于仿射函数 s u m ( w ⊗ x ) sum(\mathbf{w}\otimes\mathbf{x}) sum(w⊗x) 和激活函数 m a x ( 0 , x ) max(0, \mathbf{x}) max(0,x) 下一节会介绍他的导数。下图给出了Jacobian的形状。(长方形形状表示标量/行向量/列向量/矩阵)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MvKEc0TW-1601559616707)(https://raw.githubusercontent.com/lih627/MyPicGo/master/imgs/20201001001119.png)]
神经激活函数的梯度
下面了来计算神经网络激活函数的导数,包括参数
w
\mathbf{w}
w 和
b
b
b (注意$\mathbf{x} $ 和
w
\mathbf{w}
w 都是列向量):
a
c
t
i
v
a
t
i
o
n
(
x
)
=
m
a
x
(
0
,
w
⋅
x
+
b
)
activation(\mathbf{x})=max(0, \mathbf{w}\cdot\mathbf{x} + b)
activation(x)=max(0,w⋅x+b)
上述表示全连接层在接一个线形整流单元作为激活函数。首先忽略
m
a
x
max
max 函数,计算
∂
∂
w
(
w
⋅
x
+
b
)
\frac{\partial}{\partial\mathbf{w}}(\mathbf{w\cdot x} + b)
∂w∂(w⋅x+b) 和
∂
∂
b
(
w
⋅
x
+
b
)
\frac{\partial}{\partial b}(\mathbf{w\cdot x} + b)
∂b∂(w⋅x+b) 。首先考虑
w
⋅
x
\mathbf{w\cdot x}
w⋅x 。其实就是元素对应位置的乘积的和。 即
∑
i
n
(
w
i
x
i
)
=
s
u
m
(
w
⊗
x
)
\sum_{i}^n(w_ix_i)=sum(\mathbf{w\otimes x})
∑in(wixi)=sum(w⊗x) 。或者采用线性代数的表达方式
w
⋅
x
=
w
T
x
\mathbf{w\cdot x} = \mathbf{w}^T\mathbf{x}
w⋅x=wTx 。在上面章节已经讨论过了
s
u
m
(
x
)
sum(\mathbf{x})
sum(x) 和
w
⊗
x
\mathbf{w\otimes x }
w⊗x 的偏导数了。在这里使用链式法则:
u = w ⊗ x y = s u m ( u ) \begin{aligned} \mathbf{u} &= \mathbf{w\otimes x}\\ y &= sum(\mathbf{u}) \end{aligned} uy=w⊗x=sum(u)
计算偏导数:
∂
u
∂
w
=
∂
∂
w
(
w
⊗
x
)
=
d
i
a
g
(
x
)
∂
y
∂
u
=
∂
∂
u
s
u
m
(
u
)
=
1
⃗
T
\begin{aligned} \frac{\partial\mathbf{u}}{\partial \mathbf{w}} &= \frac{\partial}{\partial \mathbf{w}}(\mathbf{w\otimes x}) = diag(\mathbf{x})\\ \frac{\partial y}{\partial\mathbf{u}} &= \frac{\partial}{\partial \mathbf{u}}sum(\mathbf{u}) =\vec{1}^T \end{aligned}
∂w∂u∂u∂y=∂w∂(w⊗x)=diag(x)=∂u∂sum(u)=1T
通过链式法则可得:
∂
y
∂
w
=
∂
y
∂
u
∂
u
∂
w
=
1
⃗
T
d
i
a
g
(
x
)
=
x
T
\frac{\partial y}{\partial \mathbf{w}} = \frac{\partial y}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{w}} = \vec{1}^Tdiag(\mathbf{x}) = \mathbf{x}^T
∂w∂y=∂u∂y∂w∂u=1Tdiag(x)=xT
因此有:
∂
y
∂
w
=
[
x
1
,
⋯
,
x
n
]
=
x
T
\frac{\partial y}{\partial \mathbf{w}} = [x_1, \cdots, x_n] = \mathbf{x}^T
∂w∂y=[x1,⋯,xn]=xT
现在考虑
y
=
w
⋅
x
+
b
y=\mathbf{w\cdot x} + b
y=w⋅x+b 需要考虑两个偏导,并且不需要链式法则:
∂
y
∂
w
=
∂
∂
w
w
⋅
x
+
∂
∂
w
b
=
x
T
+
0
⃗
T
=
x
T
∂
y
∂
b
=
∂
∂
b
w
⋅
x
+
∂
∂
b
b
=
0
+
1
=
1
\begin{aligned} \frac{\partial y}{\partial \mathbf{w}} &= \frac{\partial}{\partial\mathbf{w}}\mathbf{w\cdot x} + \frac{\partial}{\partial \mathbf{w}}b = \mathbf{x}^T + \vec{0}^T = \mathbf{x}^T\\ \frac{\partial y}{\partial b} &= \frac{\partial}{\partial b} \mathbf{w\cdot x} + \frac{\partial}{\partial b} b = 0 + 1 = 1 \end{aligned}
∂w∂y∂b∂y=∂w∂w⋅x+∂w∂b=xT+0T=xT=∂b∂w⋅x+∂b∂b=0+1=1
下面需要考虑
m
a
x
(
0
,
z
)
max(0, z)
max(0,z) 函数的导数, 显然
KaTeX parse error: Unknown column alignment: * at position 63: …\begin{array} {*̲*lr**} 0 &z\le …
当计算加激活函数后的梯度时,使用向量链式法则;
z
(
w
,
b
,
x
)
=
w
⋅
x
+
b
a
c
t
i
v
a
t
i
o
n
(
z
)
=
m
a
x
(
0
,
z
)
\begin{aligned} z(\mathbf{w}, b, \mathbf{x}) &= \mathbf{w\cdot x} + b\\ activation(z) &= max(0, z) \end{aligned}
z(w,b,x)activation(z)=w⋅x+b=max(0,z)
链式法则表达为:
∂
a
c
t
i
v
a
t
i
o
n
∂
w
=
∂
a
c
t
i
v
a
a
t
i
o
n
∂
z
∂
z
∂
w
\frac{\partial activation}{\partial \mathbf{w}} = \frac{\partial activaation}{\partial z} \frac{\partial z}{\partial \mathbf{w}}
∂w∂activation=∂z∂activaation∂w∂z
带入表达式为:
∂
a
c
t
i
v
a
t
i
o
n
∂
w
=
{
0
∂
z
∂
w
=
0
⃗
T
w
⋅
x
+
b
≤
0
1
∂
z
∂
w
=
x
T
w
⋅
x
+
b
>
0
\frac{\partial activation}{\partial \mathbf{w}} = \left\{ \begin{array}{ll} 0\frac{\partial z}{\partial w} = \vec{0}^T & \mathbf{w\cdot x} + b \le 0\\ 1\frac{\partial z}{\partial\mathbf{w}}=\mathbf{x}^T & \mathbf{w\cdot x} + b>0 \end{array} \right.
∂w∂activation={0∂w∂z=0T1∂w∂z=xTw⋅x+b≤0w⋅x+b>0
同理:
KaTeX parse error: Expected & or \\ or \cr or \end at position 66: …\begin{array}ll}̲ 0\frac{\partia…
拓展: 广播函数
当使使用广播函数(board casting functions) 时,此时
m
a
x
max
max 输入的参数为向量。只需要对向量中的每一个元素做标量的
m
a
x
max
max 运算。即:
m
a
x
(
0
,
x
)
=
[
m
a
x
(
0
,
x
1
)
m
a
x
(
0
,
x
2
)
⋮
m
a
x
(
0
,
x
n
)
]
max(0,\mathbf{x}) = \begin{bmatrix} max(0, x_1)\\ max(0, x_2)\\ \vdots\\ max(0, x_n) \end{bmatrix}
max(0,x)=⎣⎢⎢⎢⎡max(0,x1)max(0,x2)⋮max(0,xn)⎦⎥⎥⎥⎤
此时梯度为:
∂
∂
x
m
a
x
(
0
,
x
)
=
[
∂
∂
x
1
m
a
x
(
0
,
x
1
)
∂
∂
x
2
m
a
x
(
0
,
x
2
)
⋮
∂
∂
x
n
m
a
x
(
0
,
x
n
)
]
\frac{\partial}{\partial \mathbf{x}} max(0, \mathbf{x}) = \begin{bmatrix} \frac{\partial}{\partial x_1}max(0, x_1)\\ \frac{\partial}{\partial x_2}max(0, x_2)\\ \vdots\\ \frac{\partial}{\partial x_n}max(0, x_n) \end{bmatrix}
∂x∂max(0,x)=⎣⎢⎢⎢⎡∂x1∂max(0,x1)∂x2∂max(0,x2)⋮∂xn∂max(0,xn)⎦⎥⎥⎥⎤
神经网络损失函数的梯度
损失函数的结果是一个标量,先进行符号定义 每个样本和标签被定义为
(
x
i
,
t
a
r
g
e
t
(
x
i
)
)
(\mathbf{x}_i, target(\mathbf{x}_i))
(xi,target(xi)) 有:
X
=
[
x
1
,
x
2
,
⋯
,
x
N
]
T
X=[\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N]^T
X=[x1,x2,⋯,xN]T
其中
N
=
∣
X
∣
N=|X|
N=∣X∣, 标签构成的向量为:
y
=
[
t
a
r
g
e
t
(
x
1
)
,
t
a
r
g
e
t
(
x
2
)
,
⋯
,
t
a
r
g
e
t
(
x
N
)
]
T
\mathbf{y} = [target(\mathbf{x}_1), target(\mathbf{x}_2), \cdots, target(\mathbf{x}_N)]^T
y=[target(x1),target(x2),⋯,target(xN)]T
其中
y
i
y_i
yi 是标量。损失函数被定义为:
C
(
w
,
b
,
X
,
y
)
=
1
N
∑
i
=
1
N
(
y
i
−
a
c
t
i
v
a
t
i
o
n
(
x
i
)
)
2
=
1
N
∑
i
=
1
N
(
y
i
−
m
a
x
(
w
⋅
x
i
+
b
)
)
2
C(\mathbf{w}, b, X,\mathbf{y})= \frac{1}{N}\sum_{i = 1}^N(y_i - activation(\mathbf{x}_i))^2= \frac{1}{N}\sum_{i = 1}^N(y_i - max(\mathbf{w\cdot x}_i + b))^2
C(w,b,X,y)=N1i=1∑N(yi−activation(xi))2=N1i=1∑N(yi−max(w⋅xi+b))2
根据链式法则:
u
(
w
,
b
,
x
)
=
m
a
x
(
0
,
w
⋅
x
+
b
)
v
(
y
,
u
)
=
y
−
u
C
(
v
)
=
1
N
∑
i
=
1
N
v
2
\begin{aligned} u(\mathbf{w}, b, \mathbf{x}) &= max(0, \mathbf{w\cdot x} + b)\\ v(y, u) &= y - u\\ C(v) &= \frac{1}{N}\sum_{i = 1}^N v^2 \end{aligned}
u(w,b,x)v(y,u)C(v)=max(0,w⋅x+b)=y−u=N1i=1∑Nv2
关于权重的梯度
从前几章节可以知道:
∂
∂
w
u
(
w
,
b
,
x
)
=
{
0
⃗
T
w
⋅
x
+
b
≤
0
x
T
w
⋅
x
+
b
>
0
\frac{\partial}{\partial \mathbf{w}}u(\mathbf{w}, b, \mathbf{x}) = \left\{ \begin{array}{ll} \vec{0}^T & \mathbf{w\cdot x} + b\le0\\ \mathbf{x}^T & \mathbf{w\cdot x} + b> 0 \end{array} \right.
∂w∂u(w,b,x)={0TxTw⋅x+b≤0w⋅x+b>0
∂
v
(
y
,
u
)
∂
w
=
∂
∂
w
(
y
−
u
)
=
0
⃗
T
−
∂
u
∂
w
=
−
∂
u
∂
w
=
{
0
⃗
T
w
⋅
x
+
b
≤
0
−
x
T
w
⋅
x
+
b
>
0
\frac{\partial v(y, u)}{\partial \mathbf{w}} = \frac{\partial}{\partial\mathbf{w}}(y - u) = \vec{0}^T - \frac{\partial u}{\partial \mathbf{w}}= -\frac{\partial u}{\partial\mathbf{w}} = \left\{ \begin{array}{ll} \vec{0}^T & \mathbf{w\cdot x} + b \le 0\\ -\mathbf{x}^T &\mathbf{w\cdot x} + b > 0 \end{array} \right.
∂w∂v(y,u)=∂w∂(y−u)=0T−∂w∂u=−∂w∂u={0T−xTw⋅x+b≤0w⋅x+b>0
那总的梯度可以通过下式子计算:
∂
C
(
v
)
∂
w
=
∂
∂
w
1
N
∑
i
=
1
N
v
2
=
1
N
∑
i
=
1
N
∂
v
2
∂
w
=
1
N
∑
i
=
1
N
2
v
∂
v
∂
w
=
1
N
∑
i
=
1
N
{
2
v
0
⃗
T
=
0
⃗
T
w
⋅
x
i
+
b
≤
0
−
2
v
x
T
w
⋅
x
i
+
b
>
0
=
1
N
∑
i
=
1
N
{
0
⃗
T
w
⋅
x
i
+
b
≤
0
−
2
(
y
i
−
u
)
x
i
T
w
⋅
x
+
i
+
b
>
0
=
1
N
∑
i
=
1
N
{
0
⃗
T
w
⋅
x
i
+
b
≤
0
−
2
(
y
i
−
m
a
x
(
0
,
w
⋅
x
+
i
+
b
)
)
x
i
T
w
⋅
x
i
+
b
>
0
=
{
0
⃗
T
w
⋅
x
i
+
b
≤
0
−
2
N
∑
i
=
1
N
(
y
i
−
(
w
⋅
x
i
+
b
)
)
x
i
T
w
⋅
x
i
+
b
>
0
=
{
0
⃗
T
w
⋅
x
i
+
b
≤
0
2
N
∑
i
=
1
N
(
w
⋅
x
i
+
b
−
y
i
)
x
i
T
w
⋅
x
i
+
b
>
0
\begin{aligned} \frac{\partial C(v)}{\partial \mathbf{w}} &= \frac{\partial}{\partial \mathbf{w}}\frac{1}{N} \sum_{i= 1}^N v^2\\ &= \frac{1}{N}\sum_{i=1}^N\frac{\partial v^2}{\partial \mathbf{w}} \\&= \frac{1}{N}\sum_{i= 1}^N 2v\frac{\partial v}{\partial \mathbf{w}}\\ &= \frac{1}{N}\sum_{i = 1}^N\left\{ \begin{array}{lr} 2v\vec{0}^T = \vec{0}^T &\mathbf{w\cdot x}_i + b\le0\\ -2v\mathbf{x}^T & \mathbf{w\cdot x}_i + b > 0 \end{array} \right.\\ &= \frac{1}{N}\sum_{i=1}^N\left\{ \begin{array}{ll} \vec{0}^T & \mathbf{w\cdot x}_i + b\le 0\\ -2(y_i - u)\mathbf{x}_i^T &\mathbf{w\cdot x}+i + b >0 \end{array} \right.\\ &= \frac{1}{N}\sum_{i=1}^N\left\{ \begin{array}{ll} \vec{0}^T &\mathbf{w\cdot x}_i + b\le 0\\ -2(y_i - max(0,\mathbf{w\cdot x}+i + b))\mathbf{x}_i^T & \mathbf{w\cdot x}_i + b> 0 \end{array} \right.\\ &= \left\{ \begin{array}{ll} \vec{0}^T & \mathbf{w\cdot x}_i + b \le 0\\ \frac{-2}{N}\sum_{i= 1}^N(y_i - (\mathbf{w\cdot x}_i + b))\mathbf{x}_i^T &\mathbf{w\cdot x}_i + b > 0 \end{array} \right.\\ &= \left\{ \begin{array}{ll} \vec{0}^T & \mathbf{w\cdot x}_i + b\le 0\\ \frac{2}{N}\sum_{i = 1}^N(\mathbf{w\cdot x}_i + b - y_i)\mathbf{x}_i^T & \mathbf{w\cdot x}_i + b > 0 \end{array} \right. \end{aligned}
∂w∂C(v)=∂w∂N1i=1∑Nv2=N1i=1∑N∂w∂v2=N1i=1∑N2v∂w∂v=N1i=1∑N{2v0T=0T−2vxTw⋅xi+b≤0w⋅xi+b>0=N1i=1∑N{0T−2(yi−u)xiTw⋅xi+b≤0w⋅x+i+b>0=N1i=1∑N{0T−2(yi−max(0,w⋅x+i+b))xiTw⋅xi+b≤0w⋅xi+b>0={0TN−2∑i=1N(yi−(w⋅xi+b))xiTw⋅xi+b≤0w⋅xi+b>0={0TN2∑i=1N(w⋅xi+b−yi)xiTw⋅xi+b≤0w⋅xi+b>0
可以定义一个误差项
e
i
=
w
⋅
x
i
+
b
−
y
i
e_i = \mathbf{w\cdot x}_i + b - y_i
ei=w⋅xi+b−yi 来简化总梯度。注意该梯度针对激活函数结果非0的情况:
∂
C
∂
w
=
2
N
∑
i
=
1
N
e
i
x
i
T
w
⋅
x
i
+
b
>
0
\frac{\partial C}{\partial\mathbf{w}}=\frac{2}{N}\sum_{i = 1}^Ne_i\mathbf{x_i}^T \quad \mathbf{w\cdot x}_i + b > 0
∂w∂C=N2i=1∑NeixiTw⋅xi+b>0
注意此时梯度是通过所有样本计算的加权平均项。权重与误差项相关。最终的梯度指向更大的
e
i
e_i
ei 对应样本的方向。梯度下降公式写作
w
t
+
1
=
w
t
−
η
∂
C
∂
w
\mathbf{w}_{t + 1} = \mathbf{w}_t - \mathbf{\eta}\frac{\partial C}{\partial\mathbf{w}}
wt+1=wt−η∂w∂C
针对偏置项的公式
优化偏置项
b
b
b 和优化权重项类似, 先使用中间变量
u
(
w
,
b
,
x
)
=
m
a
x
(
0
,
w
⋅
x
+
b
)
v
(
y
,
u
)
=
y
−
i
C
(
v
)
=
1
N
∑
i
=
1
N
v
2
\begin{aligned} u(\mathbf{w}, b, \mathbf{x}) &= max(0, \mathbf{w\cdot x} + b)\\ v(y, u) &= y - i\\ C(v) &= \frac{1}{N}\sum_{i=1}^N v^2 \end{aligned}
u(w,b,x)v(y,u)C(v)=max(0,w⋅x+b)=y−i=N1i=1∑Nv2
已知:
∂
u
∂
b
=
{
0
w
⋅
x
+
b
≤
0
1
w
⋅
x
+
b
>
0
\frac{\partial u}{\partial b} = \left\{ \begin{array}{ll} 0 & \mathbf{w\cdot x} + b \le 0\\ 1 & \mathbf{w\cdot x} + b> 0 \end{array} \right.
∂b∂u={01w⋅x+b≤0w⋅x+b>0
那么对于
v
v
v , 其偏导数为:
∂
v
(
y
,
u
)
∂
b
=
−
∂
u
∂
b
=
{
0
w
⋅
x
+
b
≤
0
−
1
w
⋅
x
+
b
>
0
\frac{\partial v(y, u)}{\partial b} = -\frac{\partial u}{\partial b} = \left\{ \begin{array}{ll} 0 & \mathbf{w\cdot x} + b \le 0\\ -1 & \mathbf{w\cdot x} + b > 0 \end{array} \right.
∂b∂v(y,u)=−∂b∂u={0−1w⋅x+b≤0w⋅x+b>0
那么总的偏导数为
∂
C
(
v
)
∂
b
=
∂
∂
b
1
N
∑
i
=
1
N
v
2
=
1
N
∑
i
=
1
N
∂
∂
b
v
2
=
1
N
∑
i
=
1
N
2
v
∂
v
∂
b
=
1
N
∑
i
=
1
N
{
0
w
⋅
x
+
b
≤
0
−
2
v
w
⋅
x
+
b
>
0
=
1
N
∑
i
=
1
N
{
0
w
⋅
x
+
b
≤
0
−
2
(
y
i
−
m
a
x
(
0
,
w
⋅
x
i
+
b
)
w
⋅
x
+
b
>
0
=
{
0
w
⋅
x
+
b
≤
0
2
N
∑
i
=
1
N
2
(
w
⋅
x
i
+
b
−
y
i
)
w
⋅
x
i
+
b
>
0
\begin{aligned} \frac{\partial C(v)}{\partial b} &= \frac{\partial}{\partial b}\frac{1}{N} \sum_{i = 1}^Nv ^ 2\\ &= \frac{1}{N}\sum_{i = 1}^N \frac{\partial}{\partial b} v^2\\ &= \frac{1}{N}\sum_{i = 1}^N 2v\frac{\partial v}{\partial b}\\ &= \frac{1}{N}\sum_{i = 1}^N\left\{ \begin{array}{ll} 0 & \mathbf{w\cdot x} + b\le 0\\ -2v & \mathbf{w\cdot x} + b > 0 \end{array} \right.\\ &= \frac{1}{N}\sum_{i = 1}^N\left\{ \begin{array}{ll} 0 & \mathbf{w\cdot x} + b \le 0\\ -2(y_i - max(0, \mathbf{w\cdot x}_i + b) &\mathbf{w \cdot} x + b > 0 \end{array} \right. \\ &= \left\{ \begin{array}{ll} 0 & \mathbf{w\cdot x} + b \le 0\\ \frac{2}{N}\sum_{i = 1}^N2(\mathbf{w\cdot x}_i + b - y_i) &\mathbf{w \cdot x}_i + b > 0 \end{array} \right. \end{aligned}
∂b∂C(v)=∂b∂N1i=1∑Nv2=N1i=1∑N∂b∂v2=N1i=1∑N2v∂b∂v=N1i=1∑N{0−2vw⋅x+b≤0w⋅x+b>0=N1i=1∑N{0−2(yi−max(0,w⋅xi+b)w⋅x+b≤0w⋅x+b>0={0N2∑i=1N2(w⋅xi+b−yi)w⋅x+b≤0w⋅xi+b>0
同理通过定于误差项
e
i
=
w
⋅
x
i
+
b
−
y
i
e_i = \mathbf{w\cdot x}_i + b - y_i
ei=w⋅xi+b−yi
可以得到偏导数为
∂
C
∂
b
=
2
N
∑
i
=
1
N
e
i
w
⋅
x
i
+
b
>
0
\frac{\partial C}{\partial b} = \frac{2}{N}\sum_{i = 1}^Ne_i \quad \mathbf{w\cdot x}_i + b > 0
∂b∂C=N2i=1∑Neiw⋅xi+b>0
对应的更新公式为
b
t
+
1
=
b
t
−
η
∂
C
∂
b
b_{t + 1} = b_t - \mathbf{\eta}\frac{\partial C}{\partial b}
bt+1=bt−η∂b∂C
总结
在实际使用过程中,通常使用扩充权重向量。即
w
^
=
[
w
T
,
b
]
T
x
^
=
[
x
T
,
1
]
\begin{aligned} \hat{\mathbf{w}} &= [\mathbf{w}^T, b]^T\\ \hat{\mathbf{x}} & = [\mathbf{x}^T, 1] \end{aligned}
w^x^=[wT,b]T=[xT,1]
此时
w
⋅
x
+
b
=
w
^
⋅
x
^
\mathbf{w\cdot x} + b = \hat{\mathbf{w}}\cdot \hat{\mathbf{x}}
w⋅x+b=w^⋅x^






















 1316
1316











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








