统计-5 事件关系

往往我们感兴趣的复杂事件是由多个简单的事件组成的，这些简单事件比复杂事件清晰易计算，因此只要搞清楚这些简单事件和复杂事件的关系，那可以简单事件的计算来得到复杂事件的概率了；下面是几类关系，事件本身是集合，因此也是事件集合的关系

1. 事件的包含和相等

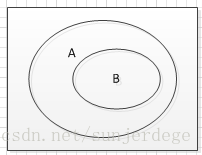
事件A包括事件B，代表A发生则B必然发生，

若 ，则A = B；

证明A和B相等的方法是假设A发生，则推出B发生；然后假设B发生，然后能退出A发生；

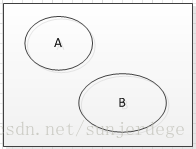
2.      事件的互斥与对立

互斥：A和B不再同一次试验中发生；

对立：A和B互斥，且A+B = 全部试验结果；

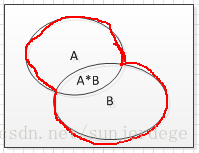
3.      事件的和（并）

C = A + B；事件C发生 = A发生或者 B 发生；

注：这里是集合运算，因此A和B的交集A只算一次；

4.      概率的加法

互斥事件和的概率 = 互斥事件概率的和

P（A1 + A2 + …） = P(A1) + P(A2) + …

A1，A2是互斥事件

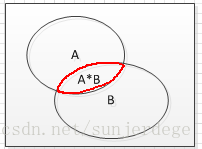
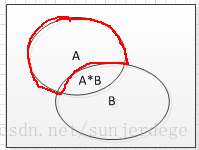
5.      事件的积

C = AB；C事件 = A和B都发生

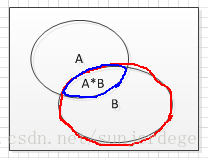
6.      事件的差

C = A – B；C事件 = A发生且B不发生

7.      条件概率，顾名思义，就是在一定条件下的概率，若有事件A，B，则在给定B发生的条件下A的条件概率，记为P(A|B) = P(AB) / P(B)；

8.      事件的独立性/概率乘法

若P(A|B) = P(A)，则说明，A发生的概率和B发生下A发生的概率一样，就说明B和A没啥关系，B发不发生对A没影响；这时，称A和B两事件相互独立，则：

                  P(AB)= P(A) * P(B)

9.      全概率公式

全概率公式解决的是当我们对一个事件的发生没有头绪时，把将之分解为在某一事件各种发生条件下的小事件；

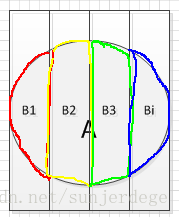
全部试验结果：B = B1+ B2 + B3 ...，B1、B2。。。互斥；

A = A * (B1 + B2 + B3 + …) = A*B1 +A*B2 + A*B3

P(A) = P(A*B1) + P(A*B2) + …

         =P(A/B1)*P(B1)+ P(A/B2)*P(B2) + …

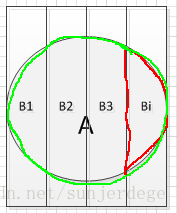
10.  贝叶斯公式

若已知A发生，则B发生的概率，P(B|A)是条件概率：

P(Bi|A) = P(ABi)/P(A) = P(A|Bi)*P(Bi)/P(A)

P(A|Bi)成为先验概率，Bi是目的事件/结果i发生，A是条件/特征事件/原因；

P(A) 通过分解B用全概率公式求解，= sum(P(Bj)*P(A|Bj))

对事件的预测，贝叶斯是由结果推测原因；全概率是由原因推结果；