神经网络涵义
神经网络定义有很多,你可以以猫为例,他不知道猫是什么,但是你把一张猫的图片给他看,他能回答你这是一只猫的图片。这其中的关键就是你和他对于猫这个标准的差异,通过你给出的标准进行对比不断修改他的标准并逐渐向你的标准靠近的过程便是训练。当然在这个过程中,你的标准便是完美标准,他的开始标准会由你初始化处理的结果来决定,所以你数据的初步处理也会对最终的结果产生影响。
损失函数定义
由上面的描述,我所认为的损失函数是你的标准与神经网络的标准相差多少的定量表达。这个具体的表达式吴恩达在他视频里有提到两个:
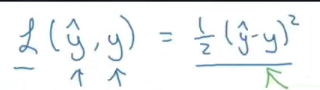
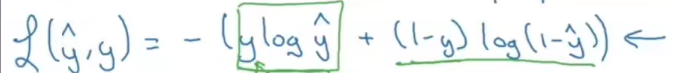
这两个表达式是如何推导出来的?首先,我们比较两个模型差距有多少一般有下面三个思路:最小二乘法,极大似然估计,交叉熵,下面分别从这三个思路来进行推导
最小二乘法
这是比较两个模型之间的差距最简单的方法,首先我们要知道直接比较模型不行,因为不仅我们想出的模型难以表达,而且神经网络里面的模型经过好几层嵌套后更加看不起看不懂,这时候最简单有效的方法就是比较结果。
还是以猫为例,假设我们有n张图片,分别将这些图片交给人脑和神经网络来判断是不是猫,有多大概率是猫,这时候便会得到
X
i
X_i
Xi和
Y
i
Y_i
Yi(分别表示在人脑和神经网络中第
i
i
i张图片是猫的概率)。
现在如果我们想知道第一张图片人脑和神经网络相差范围有多大可以通过
∣
X
1
−
Y
1
∣
|X_1 -Y_1|
∣X1−Y1∣来得到,但是我们需要的是所有图片的结果,所以我们要把这些值累加起来,这便是
∑
i
=
1
n
∣
X
i
−
Y
i
∣
\sum_{i=1}^{n} |X_i-Y_i|
∑i=1n∣Xi−Yi∣。当这个值最小的时候,即
m
i
n
∑
i
=
1
n
∣
X
i
−
Y
i
∣
min\sum_{i=1}^{n} |X_i-Y_i|
min∑i=1n∣Xi−Yi∣,我们可以认为这里的模型与人脑里的模型是近似的。理论上这样去做可以认为已经达到我们想要的,就是把他们之间的差值找出来。但是,因为我们求的是绝对值,而绝对值在其定义域上不一定是全程可导的,这时候可以通过求绝对值的平方来解决,即
m
i
n
∑
i
=
1
n
(
X
i
−
Y
i
)
2
min\sum_{i=1}^{n} (X_i-Y_i)^2
min∑i=1n(Xi−Yi)2。求平方之后,我们要明白虽然最后的值发生了改变,但是这并不影响
X
i
X_i
Xi和
Y
i
Y_i
Yi的关系,并且全程可导。到这里我们不难看出为什么这要叫最小二乘法。
现在对比第一张图片的表达式
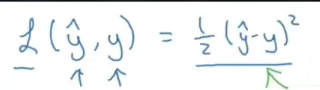
- 这里的 y ^ − y \hat{y}-y y^−y便是我们上面提到的 X i − Y i X_i-Y_i Xi−Yi
- 这里的 1 2 \frac{1}{2} 21是方便后面求导时能够与指数2相乘消掉
- 这里没有 ∑ \sum{} ∑,主要是因为训练时,神经网络是一个图片一个图片逐个输入用迭代的方法来得到这个最小值,而我们上面的式子是数学表达式并没有迭代的过程,但是两者没有本质的差别。
到这里,我们可以知道吴恩达给出的损失函数第一个式子是通过最小二乘法得出的结果。如果只是用它来判断两个概率模型之间的差距有多少还是可以的。但是,在后面吴恩达有提到,用它作为损失函数进行梯度下降的时候会特别麻烦,并不推荐。
极大似然估计(最大似然估计)
这是在统计里常用的方法,似然 (likehood),你可以认为是通过结果去寻找该结果发生的最可能的原因,是一种概率的反向应用。
最简单的例子就是投硬币,假设我们投10个硬币求有多少硬币是正面,有多少硬币是反面,当然其概率模型理论上正的反的都是
50
%
50\%
50%,但是如果我们不知道这个概率模型要通过一次次投硬币来求,你能肯定每一次都能投出5个是正的5个是反的吗?这当然不能,这其中可能有7个是正的,可能有8个,也有可能全是正的。这时候我们就要比较各种情况下得到的条件概率,由于这不是这个模型的真实概率,而是我们通过投硬币出现的实际情况下计算出来的,我们也将其称为似然值。这些似然值所代表的就是实际投硬币各种情况的可能性。
到这里,我们便能知道极大似然估计便是找似然值的最大值。因为虽然我们不知道投硬币本来的概率模型是怎么样的,但是选择似然值最大所代表的概率模型便是最有可能的,最接近的模型。
又回到猫的例子,在神经网络中这逐渐输入的一张张图片类似于投硬币,而将神经网络的概率模型逐渐逼近人脑中的概率模型这一过程是不是与上面描述的很像。现在,假设人脑里的概率模型是一个高斯模型
N
(
μ
,
σ
2
)
N(\mu ,\sigma ^2)
N(μ,σ2),那么我们训练的时候就是用神经网络各种模型去匹配人脑中的模型,匹配过程就是尽量调整图像使之重合,这时候就是调整这个参数。但是在实际中,人脑中这个概率模型我们可能不清楚,甚至并不知道。然而,在神经网络中我们可以用叠加感知机的方法任意逼近一种概率模型,即便是我们不知道的模型也能逼近。现在,我们用神经网络参数的方式重新表达这个模型,即
N
N
(
W
,
b
2
)
NN(W,b^2)
NN(W,b2)(
W
W
W是未知的系数的集合,
b
b
b是偏置系数的集合),最后想要达到的结果,就用这个模型去逼近人脑那个概率模型。理论上,只要感知机足够多,人脑任何一种概率模型都能达到这样的结果。
如果
1
1
1代表图片是猫,
0
0
0则不是,那我们能得到这样一个式子:
P
(
X
1
,
X
2
,
.
.
.
,
X
n
∣
W
,
b
)
=
∏
i
=
1
n
P
(
X
i
∣
W
,
b
)
P(X_1,X_2,...,X_n|W,b)=\prod_{i=1}^{n} P(X_i|W,b)
P(X1,X2,...,Xn∣W,b)=∏i=1nP(Xi∣W,b)
(
1
)
(1)
(1)
其中,
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn代表判断图片是不是猫,
W
,
b
W,b
W,b代表神经网络中的概率模型
这个式子计算得到的值就是神经网络的似然值,当这个值最大的时候,我们就能认为神经网络里面的模型与人脑中的模型是最接近的。然而,在这里面有一个问题,就是在训练时
W
,
b
W,b
W,b是一个确定的值,无论输入怎么样的照片都是确定的,这对我们后面判断的标签,如果都是用猫的图片来确定的话,那都是
1
1
1,这样是没有办法进行训练的。也就是说,极大似然值这种程度的应用在理论上是可行的,但是却没有实际可操作性的。
这是因为我们忽略了每一次图片判断落地的结果
y
i
y_i
yi(该图片是不是猫),在训练过程中,
X
i
X_i
Xi是
1
1
1还是
0
0
0并不知道,是悬在空中的,其落地的结果就是
y
i
y_i
yi,
y
i
y_i
yi是由
W
,
b
W,b
W,b所确定的,这时候上面
(
1
)
(1)
(1)式就可以用下面的形式来表达:
P
(
X
1
,
X
2
,
.
.
.
,
X
n
∣
W
,
b
)
=
∏
i
=
1
n
P
(
X
i
∣
y
i
)
P(X_1,X_2,...,X_n|W,b)=\prod_{i=1}^{n} P(X_i|y_i)
P(X1,X2,...,Xn∣W,b)=∏i=1nP(Xi∣yi)
(
2
)
(2)
(2)
又因为图片只要
1
1
1和
0
0
0这两种可能,这就符合伯努利分布。
X i ϵ { 0 , 1 } X_i\epsilon \{0,1\} Xiϵ{0,1}
且 f ( x ) = p x ( 1 − p ) x = { p , x = 1 1 − p , x = 0 f(x)=p^x(1-p)^x=\left\{\begin{matrix} p, x=1\\ 1-p,x=0\end{matrix}\right. f(x)=px(1−p)x={p,x=11−p,x=0
由此可以通过伯努利分布将 ( 2 ) (2) (2)式展开得到下面这个式子。
P
(
X
1
,
X
2
,
.
.
.
,
X
n
∣
W
,
b
)
=
∏
i
=
1
n
y
i
X
i
(
1
−
y
i
)
1
−
X
i
P(X_1,X_2,...,X_n|W,b)=\prod_{i=1}^{n}{y_i}^{X_i}(1-y_i)^{1-X_i}
P(X1,X2,...,Xn∣W,b)=∏i=1nyiXi(1−yi)1−Xi
(
3
)
(3)
(3)
这时候我们取对数将累乘化成累加,得到
(
4
)
(4)
(4)式
l
o
g
(
∏
i
=
1
n
y
i
X
i
(
1
−
y
i
)
1
−
X
i
)
log(\prod_{i=1}^ {n}{y_i}^ {X_i}(1-y_i)^{1-X_i})
log(∏i=1nyiXi(1−yi)1−Xi)
=
∑
i
=
1
n
l
o
g
(
y
i
X
i
(
1
−
y
i
)
1
−
X
i
)
=\sum_{i=1}^{n} log({y_i}^{X_i}(1-y_i)^{1-X_i})
=∑i=1nlog(yiXi(1−yi)1−Xi)
=
∑
i
=
1
n
(
X
i
∗
l
o
g
y
i
+
(
1
−
X
i
)
∗
l
o
g
(
1
−
y
i
)
=\sum_{i=1}^{n}(X_i* logy_i + (1-X_i)*log(1-y_i)
=∑i=1n(Xi∗logyi+(1−Xi)∗log(1−yi)
(
4
)
(4)
(4)
由于 l o g log log是不会改变似然值得单调性和驻点的,所以求这个似然值的最大值也就是求 ( 4 ) (4) (4)式的最大值,也就能得到神经网络中与人脑模型最接近的概率模型,即求
m a x ( ∑ i = 1 n ( X i ∗ l o g y i + ( 1 − X i ) ∗ l o g ( 1 − y i ) ) max(\sum_{i=1}^{n}(X_i* logy_i + (1-X_i)*log(1-y_i)) max(∑i=1n(Xi∗logyi+(1−Xi)∗log(1−yi))
但是在实际计算时,我们一般回去求最小值,即:
− ( ∑ i = 1 n ( X i ∗ l o g y i + ( 1 − X i ) ∗ l o g ( 1 − y i ) ) -(\sum_{i=1}^{n}(X_i* logy_i + (1-X_i)*log(1-y_i)) −(∑i=1n(Xi∗logyi+(1−Xi)∗log(1−yi))
到这里,我们再去对比吴恩达所给出的第二个式子
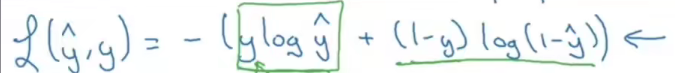
- 这里的 y ^ \hat {y} y^是神经网络的输出值,我们在上面用 y i y_i yi表示
- 这里的 y y y代表的是标签的值,便是我们上面的 X i X_i Xi
- 这里没有 ∑ \sum{} ∑,跟上一个式子解释一样与迭代有关
如果你有看吴恩达这部分视频,你会看到弹幕有不少人说这是通过交叉熵得到的,其实,通过极大似然估计和交叉熵都能推导出这式子,这并不矛盾,这就像从不同角度看同一个人有不同身份。
交叉熵
如果我们想要直接比较两个模型,则需要将这两个模型转变成同一种类型,而如何解决这个问题,这最好的例子就是货币体系,以美元做参考。相对的,对于概率模型来说,无论概率模型是什么样的,我们都可以用熵来进行统一衡量。
写到这里懒癌发作了,再加上看到这篇好文章,链接,就不写下去了,相信我后面是主要原因,等哪天我想起来再继续吧。
最后也是最重要的放张猫图。
























 4293
4293











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








