一文理解线性回归原理(模型,损失函数,正则化)

线性回归模型函数和损失函数

线性回归模型

线性回归是机器学习中最基本的问题模型了，线性回归遇到的问题一般是这样的。我们有m个样本,每个样本对应n维特征和一个结果输出,如下:
$(x_1^{(0)},x_2^{(0)},...x_n^{(0)},y_0),$
$(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1)$
$...(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$
我们的问题是对于一个新的$(x_1,x_2,...x_n)$它所对应的$y$是多少呢?如果这个问题当中y是连续的,就是一个回归问题,否则就是一个分类问题

对于n维特征的样本数据,如果我们决定使用线性回归,那么对应的模型应该是:
$h_{\theta }(X)={\theta }_0+{\theta }_1{x}_1+...{\theta }_n{x}_n,$
${\theta }_i$是模型的参数.我们增加一个$x_0=1$则可以化简为
$h_{\theta }(X)={\sum }_{i=1}^n{\theta }_i{x}_i$
$h_{theta}(X)=X\theta$ ，X是一个 $m\times n$ 的矩阵.

损失函数

一般线性回归我们使用均方误差作为损失函数。

线性回归算法

对于线性回归的损失函数$ J(\theta) = \frac{1}{2} (X\theta - Y)^T(X\theta -Y)$我们常用两种方法来求损失函数最小化的方法,一个是梯度下降法,一个是最小二乘法(其实还有一种是牛顿迭代法).这里直接给出二者的迭代公式.
梯度下降: $\theta =\theta -\alpha X^T(X\theta -Y)$
最小二乘法: $\theta =(X^{T}X{)}^{-1}{X}^{T}Y$
最小二乘法与梯度下降
##线性回归的推导:(多项式回归)
回到我们开始的线性模型,$h_{\theta }(x_1,x_2,..x_n)={\theta }_0,{\theta }_1{x}_1,...{\theta }_n{x}_n$如果这不仅仅是x的一次方,比如增加二次方,那么模型就变成了多项式回归。这里只写一个只有两个特征的p次方的多项式回归模型:

线性回归的推广:广义线性回归

线性回归的正则化

什么是过拟合？

机器学习中,如果参数过多,模型过于复杂,容易造成过拟合。即模型在训练样本数据上表现的很好,但是在实际测试样本上表现的很差,不具备良好的泛化能力。为了防止模型的过拟合化，我们在建立线性模型的时候经常需要加入正则化项。一般有L1和L2两种正则化。L1正则化的项有一个参数$\lambda$来调节损失函数的均方差项和正则化项的权重。

L1和L2正则化有何区别？

L2正则化

L2正则化比较简单,直接在原来的损失函数上增加权重的平方和
$J(\theta )=E+\lambda {\sum }_i{\theta }_i^2$
$\lambda {\sum }_i{\theta }_i^2$这个就是我们的L2正则化.
我们知道正则化的目的是限制参数过多或过大,避免模型更加复杂如10阶多项式,模型可能就过于复杂会发生过拟合。所以为了防止过拟合,我们可以将其高阶部分的权重w限制为0，这样就相当于从高阶的形式转化为低阶的.
但是这类问题属于NP难问题，我们很难直接去确定,所以我们就寻找一个相对宽松的条件,就是我们上面的L2正则化。一个更宽松的条件:
${\sum }_j{\theta }_j^2<=C$
上式对$\theta$的平方和做数值上的界定.这时候我们的目标就转化为:最小化训练样本的均方误差E,但是要遵循$\theta$的平方和小与C的条件.
请看下图:

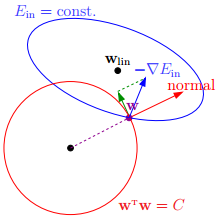
如上图所示，蓝色椭圆区域是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w 梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

L1正则化

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：
$J(\theta )=E+\lambda {\sum }_i|w_i|$
我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

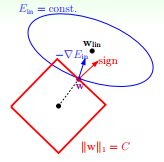
Ein 优化算法不变，$L1$ 正则化限定了 $w$ 的有效区域是一个正方形，且满足 $|w|<C$。空间中的点 w 沿着 $-\nabla E$ 的方向移动。但是，w 不能离开红色正方形区域，最多只能位于正方形边缘位置。其推导过程与 L2 类似，此处不再赘述。

L1 和 L2正则化的稀疏性

介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。
L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合


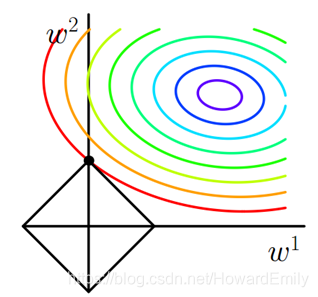
途中等值线是$J_0$的等值线,黑色方形是L1函数的图形。在图中,当$J_0$等值线与L1图形首次相交的地方就是最优解。上图中$J_0$与L在L的一个顶点处相交,这个顶点就是最优解。注意到这个定点的值是$(0,w_2)$可以直观想象,因为L函数有很多突出的定点(二维情况下四个,多为情况下更多),$J_0$与L这些顶点接触的概率肯定会远大于和其他部位接触的概率,而在这些顶点处很多权值等于0,这就是为什么L1正则化可以产生稀疏矩阵,进而用于特征选择.

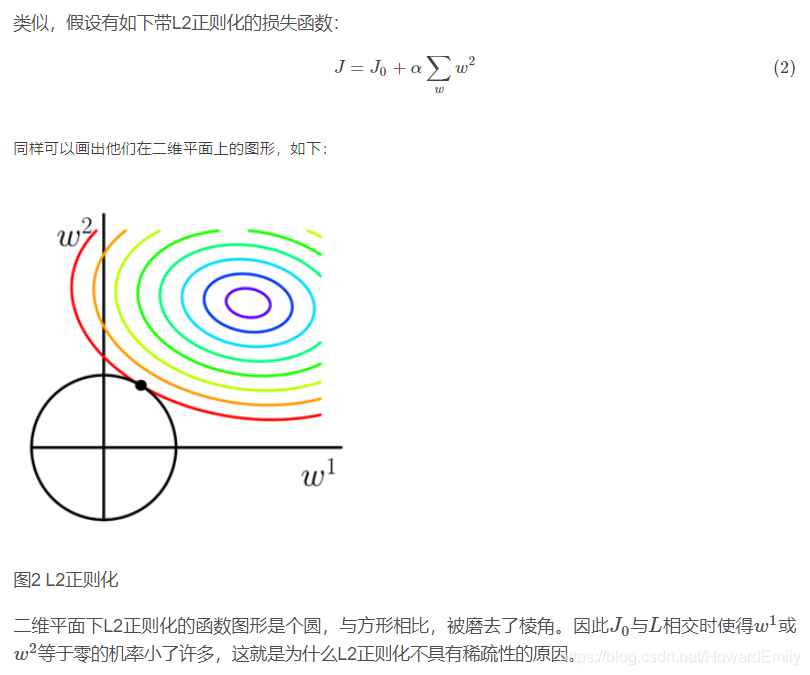
L2正则化与过拟合

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。